数学八年级下青岛版11.3图形的中心对称课件4
文档属性
| 名称 | 数学八年级下青岛版11.3图形的中心对称课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 13.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-28 13:02:19 | ||
图片预览






文档简介
课件40张PPT。第十一章:图形的平移与旋转§11.3图形的中心对称(2) 【知识与能力】
了解中心对称图形及对称中心的概念及其它们的应用。
能正确区分中心对称与中心对称图形。 教学目标 【过程与方法】
通过的观察、操作、讨论与思考使学生经历用图形的变换来描述现实生活的过程,领会类比和分类的数学思想。
通过了解中心对称图形及对称中心的概念,掌握其应用。
利用所学知识探索一个图形是中心对称图形,进一步经历观察、讨论、操作、思考、归纳和应用等认识过程。 【情感态度与价值观】
通过对中心对称图形的了解,感受数学的美,激发学习热情。
通过观察等探究过程培养学生的合作与交流的意识和探索精神。
对学生进行旋转思想的渗透。 中心对称图形的有关概念及其它们的运用。
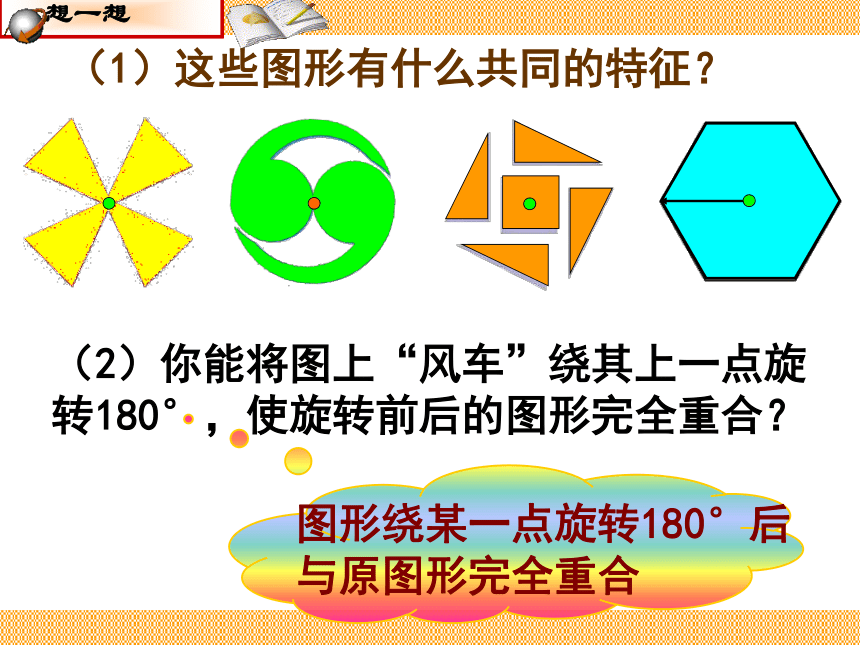
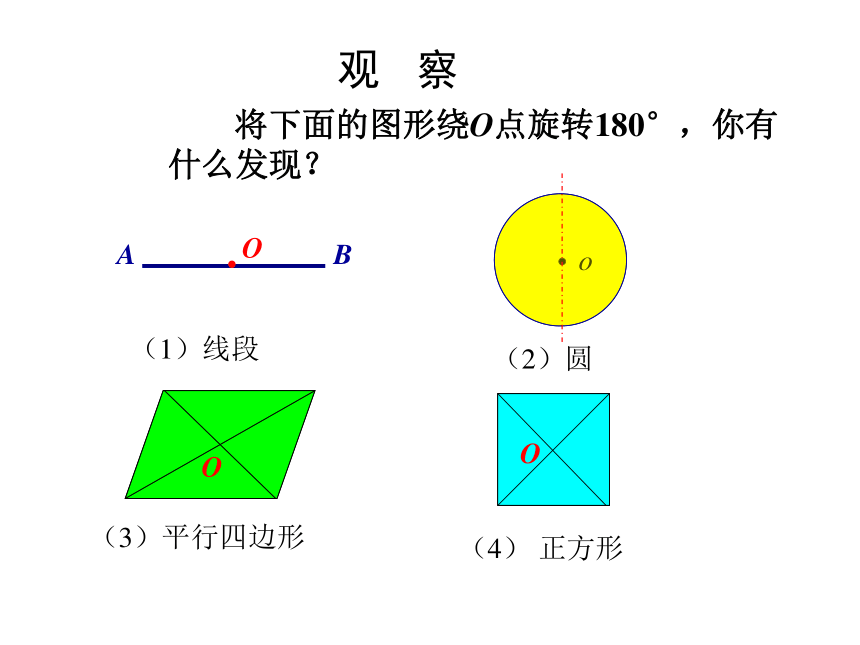
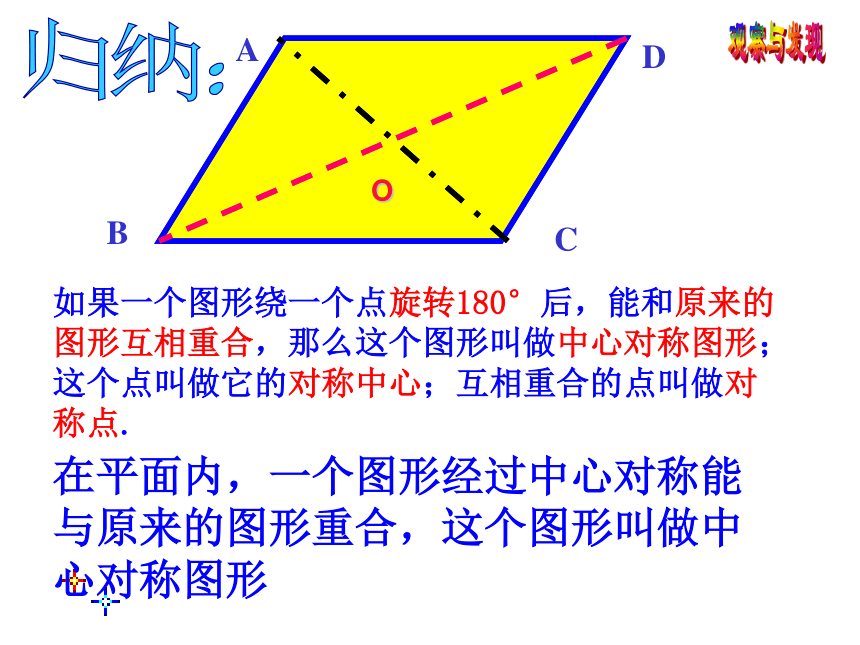
区别关于中心对称的两个图形和中心对称图形。 教学重难点(1)这些图形有什么共同的特征?(2)你能将图上“风车”绕其上一点旋转180°,使旋转前后的图形完全重合?(2)圆(4) 正方形(1)线段(3)平行四边形AB观 察 将下面的图形绕O点旋转180°,你有什么发现?OO如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点. 观察与发现BACD归纳:在平面内,一个图形经过中心对称能
与原来的图形重合,这个图形叫做中
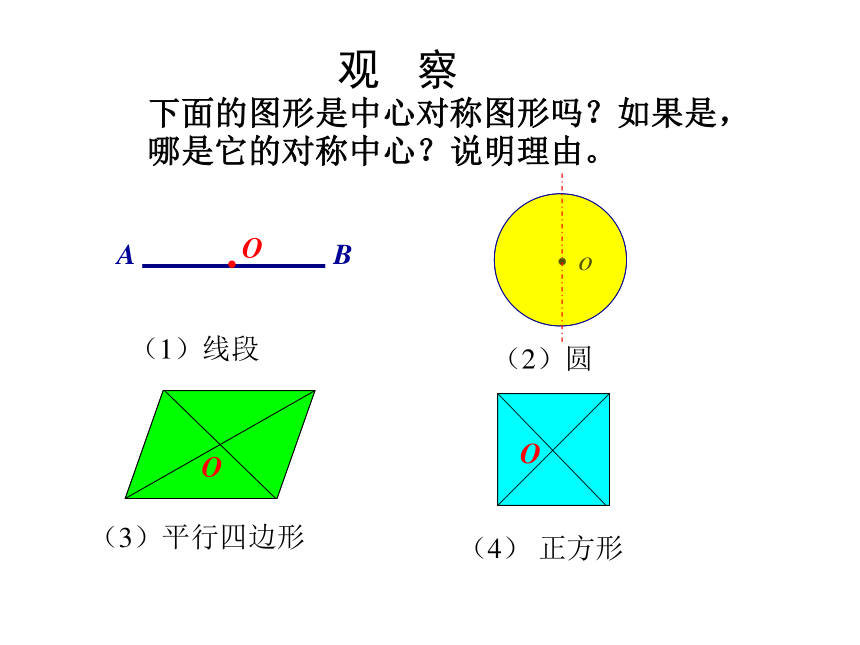
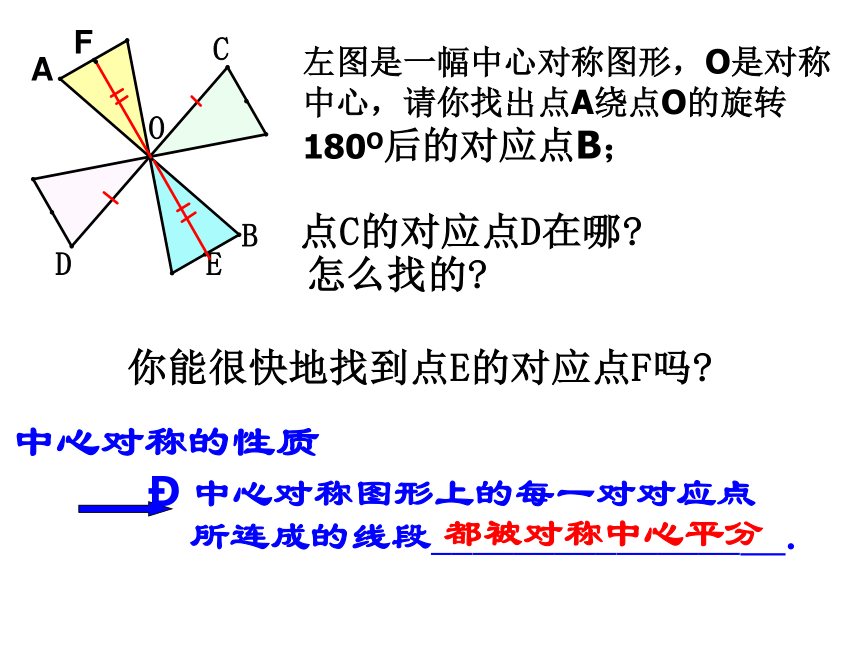
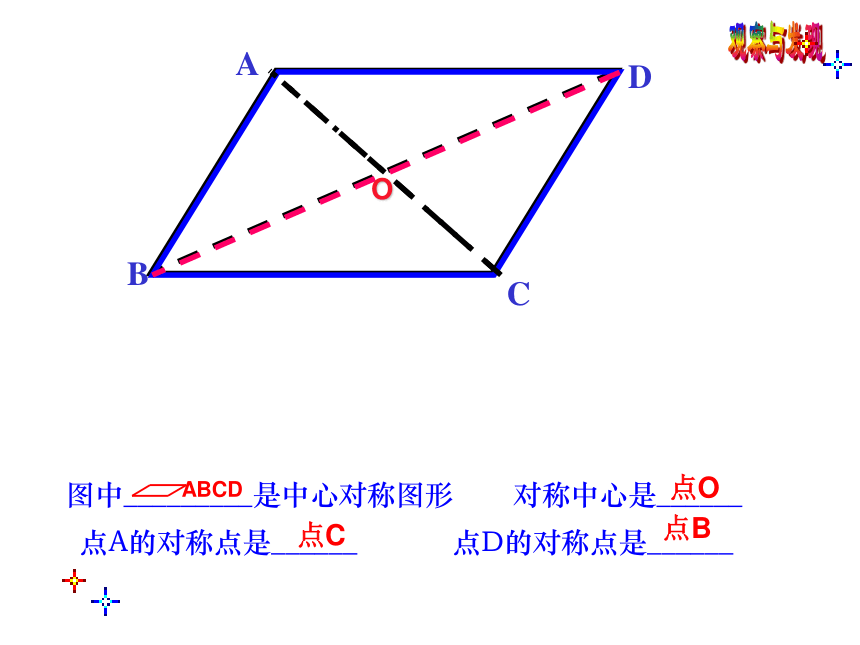
心对称图形(2)圆(4) 正方形(1)线段(3)平行四边形AB观 察下面的图形是中心对称图形吗?如果是,哪是它的对称中心?说明理由。O左图是一幅中心对称图形,O是对称中心,请你找出点A绕点O的旋转180O后的对应点B;O观察与发现BACD图中_________是中心对称图形对称中心是______点O点A的对称点是______点D的对称点是______点C点BABFCDE●AFBAFCBAFDCBAFEDCBAFO已知如图,在矩形ABCD中,AD>AB,O 为对角线的交点,过O做 一直线分别交BC,AD于M、N
(1)探索:梯形ABMN的面积是否等于梯形CDNM的面积? 如图ABCD是一块正方形的土地,要在这块土地上修筑两条笔直的互相垂直的小路,把这块土地分成面积相等的四部分,你有哪些不同的方案?画出图形,说明理由。例2: 1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形C (2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形A 随堂练习 2. 判断下列说法是否正确。 (1)轴对称图形也是中心对称图形。( ) (2)旋转对称图形也是中心对称图形。( ) (3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( ) (4)角是轴对称图形也是中心对称图形。( ) (5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )×√×√ × 3. 判断下列图形是否是中心对称图形?√ ×√√√√√√√ ×√ ×√√ ×√ ×√√√√√√ 4. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?(1)(3)(2)(4)(5)(6)(3)(4)(6)(1)(2)(5) 5. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________. ①⑤⑥⑦⑧⑨①②③④①⑥⑦⑧⑨⑥⑦⑧⑨ 6. 正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。√ ×√ ×7. 下面的扑克牌中,哪些牌面是中心对称图形?√√√对比轴对称图形与中心对称图形:有一条对称轴——直线有一个对称中心图形沿轴对折图形绕这个点旋转180O 对折部分与另一部分重合旋转后与原图重合表后-返3接下张比一比 3.如图,在矩形ABCD中,已知AB=2,AD=4,对角线AC.BD交于点O,EF经过点O交AD于点E,交BC于点F,求图中阴影部分的面积。学以致用 如图,下面一块“L”型钢板,怎样用一条直线把它分成面积相等的两个部分呢?画出草图,并说明理由.变式训练: 方案一变式训练:变式训练: 方案二变式训练: 方案三1、回顾本节课的活动过程 。2、本节课学到了哪些知识? ——应用(1)中心对称图形的定义(2)中心对称图形的性质(3)我们所学的多边形中有哪些是中心对称图形(4)中心对称图形的应用观察——分析——探索——概括? 今天你学到了什么 ? 同学们,请不要停止探究的步伐,
数学源自于对生活的热爱
……
感谢同学们, 再见!试一试正方形ABCD的边长为1,对角线AC、BD交于点O,另一个与它全等的正方形EFGO绕点O旋转,OE、OG与AB、BC分别交于点P和点Q
(1)你认为△APO与△BQO有什么关系?
(2)试求两个正方形重叠部分的面积。在旋转过程中,它们重叠部分的面积发生改变吗?若不变,你能求出来是多少吗?
了解中心对称图形及对称中心的概念及其它们的应用。
能正确区分中心对称与中心对称图形。 教学目标 【过程与方法】
通过的观察、操作、讨论与思考使学生经历用图形的变换来描述现实生活的过程,领会类比和分类的数学思想。
通过了解中心对称图形及对称中心的概念,掌握其应用。
利用所学知识探索一个图形是中心对称图形,进一步经历观察、讨论、操作、思考、归纳和应用等认识过程。 【情感态度与价值观】
通过对中心对称图形的了解,感受数学的美,激发学习热情。
通过观察等探究过程培养学生的合作与交流的意识和探索精神。
对学生进行旋转思想的渗透。 中心对称图形的有关概念及其它们的运用。
区别关于中心对称的两个图形和中心对称图形。 教学重难点(1)这些图形有什么共同的特征?(2)你能将图上“风车”绕其上一点旋转180°,使旋转前后的图形完全重合?(2)圆(4) 正方形(1)线段(3)平行四边形AB观 察 将下面的图形绕O点旋转180°,你有什么发现?OO如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点. 观察与发现BACD归纳:在平面内,一个图形经过中心对称能
与原来的图形重合,这个图形叫做中
心对称图形(2)圆(4) 正方形(1)线段(3)平行四边形AB观 察下面的图形是中心对称图形吗?如果是,哪是它的对称中心?说明理由。O左图是一幅中心对称图形,O是对称中心,请你找出点A绕点O的旋转180O后的对应点B;O观察与发现BACD图中_________是中心对称图形对称中心是______点O点A的对称点是______点D的对称点是______点C点BABFCDE●AFBAFCBAFDCBAFEDCBAFO已知如图,在矩形ABCD中,AD>AB,O 为对角线的交点,过O做 一直线分别交BC,AD于M、N
(1)探索:梯形ABMN的面积是否等于梯形CDNM的面积? 如图ABCD是一块正方形的土地,要在这块土地上修筑两条笔直的互相垂直的小路,把这块土地分成面积相等的四部分,你有哪些不同的方案?画出图形,说明理由。例2: 1. 选择题:
(1)下列图形中即是轴对称图形又是中心对称图形的是( )
A. 角 B. 等边三角形 C. 线段 D. 平行四边形C (2)下列多边形中,是中心对称图形而不是轴对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形A 随堂练习 2. 判断下列说法是否正确。 (1)轴对称图形也是中心对称图形。( ) (2)旋转对称图形也是中心对称图形。( ) (3)平行四边形、长方形和正方形都是中心对称图形,对角线的交点是它们的对称中心。( ) (4)角是轴对称图形也是中心对称图形。( ) (5)在成中心对称的两个图形中,对应线段平行(或在同一直线上)且相等。 ( )×√×√ × 3. 判断下列图形是否是中心对称图形?√ ×√√√√√√√ ×√ ×√√ ×√ ×√√√√√√ 4. 观察图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?(1)(3)(2)(4)(5)(6)(3)(4)(6)(1)(2)(5) 5. 在①线段、 ②角、 ③等腰三角形、 ④等腰梯形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形和⑨圆中,是轴对称图形的有______________
_______,是中心对称图形的有_______________,既是轴对称图形又是中心对称图形的有____________. ①⑤⑥⑦⑧⑨①②③④①⑥⑦⑧⑨⑥⑦⑧⑨ 6. 正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?边数为偶数的正多边形都是中心对称图形。√ ×√ ×7. 下面的扑克牌中,哪些牌面是中心对称图形?√√√对比轴对称图形与中心对称图形:有一条对称轴——直线有一个对称中心图形沿轴对折图形绕这个点旋转180O 对折部分与另一部分重合旋转后与原图重合表后-返3接下张比一比 3.如图,在矩形ABCD中,已知AB=2,AD=4,对角线AC.BD交于点O,EF经过点O交AD于点E,交BC于点F,求图中阴影部分的面积。学以致用 如图,下面一块“L”型钢板,怎样用一条直线把它分成面积相等的两个部分呢?画出草图,并说明理由.变式训练: 方案一变式训练:变式训练: 方案二变式训练: 方案三1、回顾本节课的活动过程 。2、本节课学到了哪些知识? ——应用(1)中心对称图形的定义(2)中心对称图形的性质(3)我们所学的多边形中有哪些是中心对称图形(4)中心对称图形的应用观察——分析——探索——概括? 今天你学到了什么 ? 同学们,请不要停止探究的步伐,
数学源自于对生活的热爱
……
感谢同学们, 再见!试一试正方形ABCD的边长为1,对角线AC、BD交于点O,另一个与它全等的正方形EFGO绕点O旋转,OE、OG与AB、BC分别交于点P和点Q
(1)你认为△APO与△BQO有什么关系?
(2)试求两个正方形重叠部分的面积。在旋转过程中,它们重叠部分的面积发生改变吗?若不变,你能求出来是多少吗?
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
