矩形的性质
图片预览







文档简介
课件27张PPT。矩形的性质 年级:八年级
学科:数学
课型:新授
授课:李祥翠 创设情境,引入新课 1.展示生活中一些平行四边形的实际应用图片,想一想:这里面应用了平行四边形的什么性质?
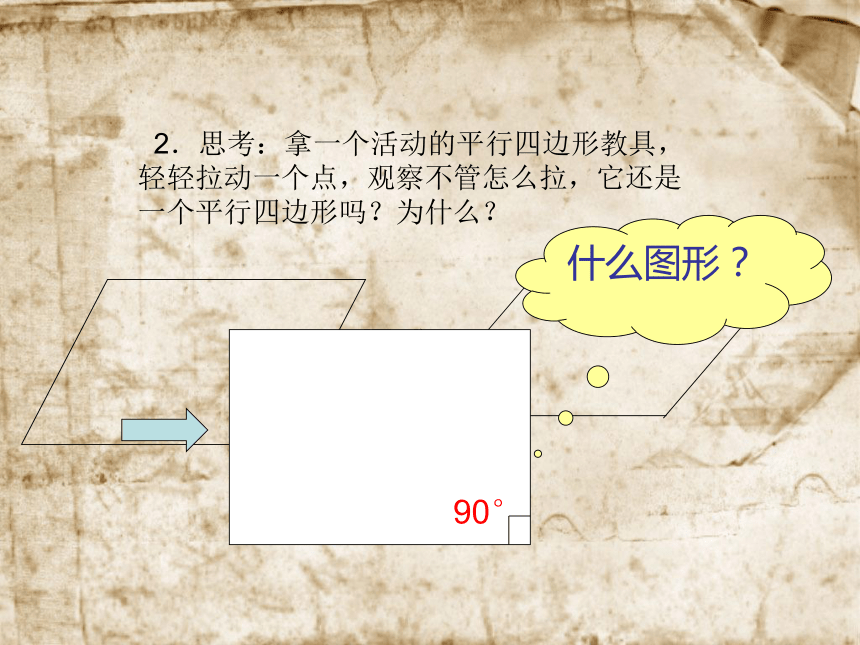
2.思考:拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?90°什么图形?教学目标:
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.
3.渗透运动联系、从量变到质变的观点.
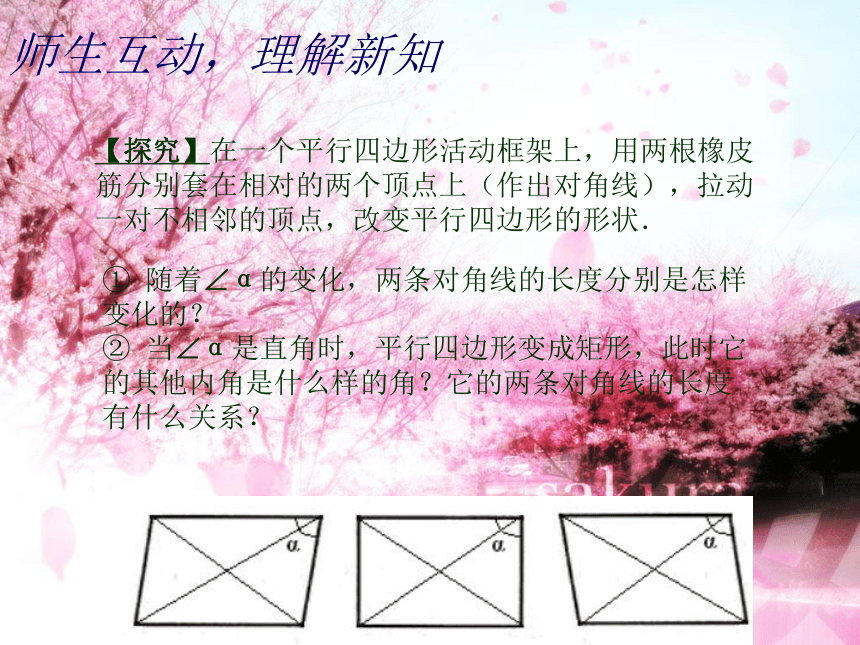
矩形的定义 有一个角是直角的平行四边形 叫做矩形,通常也叫长方形。定义中的两个条件一个角是直角平行四边形 矩形是我们最常见的图形之一,例如 门窗框、书桌面、教科书封面、地砖等都有矩形形象.想一想矩形是轴对称图形吗?它有几条对称轴? 师生互动,理解新知【探究】在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状. ① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系? 矩形性质1 矩形的四个角都是直角 已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90° A D
B C证明: ∵四边形ABCD是矩形
∴∠A=90° AD∥BC
∴∠A+∠B=180°
∴∠B=90°
∵∠A=∠C ∠B=∠D
∴∠A=∠B=∠C=∠D=90°矩形性质2 矩形的对角线相等已知:四边形ABCD是矩形
求证:AC=BDA D
B C证明: ∵四边形ABCD是矩形
∴∠ABC=∠BCD=90° AB=CD
在 △ABC和 △BCD中
AB=CD
∠ABC=∠DCB
BC=CB
∴△ABC ≌△DCB
∴ AC=BD练一练1. 如图,四边形ABCD是矩形,找出相等的线段和相等的角。 解: 相等的线段有:
AB=CD AD=BC AC=BD
OA=OB=OC=OD
相等的角有:
∠ABC=∠BCD=∠CDA=∠DAB
∠OAB=∠ABO ∠OBC=∠OCB
∠DAO=∠ADO ∠ODC=∠OCD
2. 过矩形ABCD的定点A作对角线BD的垂线,垂足为E,若BE=3.5,ED=10.5,求AB的长。A D
O
B C解: 连接AC交BD于O
∵四边形ABCD是矩形,
∴OB=OD=1/2BD OA=OC=1/2AC
∵AC=BD
∴OA=OB
∵BE=3.5 DE=10.5
∴BD=14
∴OB=OD=7
∴OE=7-3.5=3.5
∴OE=BE
∵AE⊥BD
∴AB=OA
∵OA=OB
∴OA=OB=AB
∴△AOB是等边三角形
∴AB=7OE例1已知:如图,矩形ABCD的两条对角线相交于点O, ∠AOB=60°,AB=4cm。
求矩形对角线的长. 解:∵四边形ABCD是矩形
∴OA=OC= AC
OB=OD= BD
∵AC=BD
∴OA=OB
∵∠AOB=60°
∴△AOB是等边三角形
∴OA=AB=4㎝
∴AC=BD=2OA=8㎝ 在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO=1/2AC=1/2BD.
因此可以得到直角三角形的一个性质: 直角三角形斜边上的中线等于斜边的一半 A D
O
B C练一练 如果矩形的一条对角线长为8cm,两条对角线的一个交角为120度,求矩形的边长。 A D
O
B C解:∵四边形ABCD是矩形,
∴OA=OC=1/2AC OB=OD=1/2BD
∵AC=BD
∴OA=OB
∵∠AOB=180°-120°=60°
∴△AOB是等边三角形
∴∠BAC=60° AB=OA=4㎝
∵∠ABC=90°
∴∠ACB=90°-60°=30°
在Rt△ABC中,根据勾股定理得
BC=4
∴矩形各边的长分别为4 ㎝,4㎝, 4 ㎝,4㎝尝试练习,感受新知1.填空
(1)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为________、________、________、 ________.
(2)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为________cm,________cm,________cm,________cm. 60°120°60°120°5 5 2.选择
(1)下列说法错误的是
(A)矩形的对角线互相平分 (B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形
(2)矩形的对角线把矩形分成的三角形中全等三角形一共有
(A)2对 (B)4对 (C)6对 (D)8对
(3)如图,在矩形ABCD中,AB=3,AD=4,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF=
A. B. C. D.2 CAD3. 已知BD,CE是△ABC的两条高,M,N分别是BC,DE的中点,
求证:(1)EM=DM
(2)MN⊥DE证明:
(1)连接EM DM
∵BD,CE是△ABC的高
∴∠BEC=∠BDC=90°
∵M是BC的中点
∴EM=1/2BC DM=1/2BC
∴EM=DM
(2)∵EM=DM N是ED的中点
∴MN⊥DE 课堂小结,梳理新知这节课我们学习了什么?
大家有哪些收获?深化练习,巩固新知1.矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
(A)12cm (B)10cm (C)7.5cm (D)5cm
2. 在直角三角形ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
3. 矩形是轴对称图形,它有______条对称轴.
4. 在矩形ABCD中,对角线AC,BD相交于点O,若对角线AC=10cm,边BC=8cm,则△ABO的周长为________.
5. 如图1,周长为68的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为( ).
(A)98 (B)196 (C)280 (D)284
6.如图2,根据实际需要,要在矩形实验田里修一条公路(小路任何地方水平宽度都相等),则剩余实验田的面积为________.
7.如图3,在矩形ABCD中,M是BC的中点,且MA⊥MD.若矩形ABCD的周长为48cm,则矩形ABCD的面积为_______图1图2图38. 已知,如图,矩形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OB的中点.
(1)求证:△ADE≌△BCF;
(2)若AD=4cm,AB=8cm,求OF的长.9. 如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边的中点F处,折痕为AE。
求CE的长.10. 已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.
求 AD的长及点A到BD的距离AE的长.A D
E
B C开放练习,拓展新知阅读下列过程:
如图①,小肖过AB,CD的中点画直线EF,把矩形ABCD分割成甲、乙两部分.
如图②,小徐过A,C两点画直线AC,把矩形ABCD分割成丙、丁两部分.
回答下列问题:
(1)填空:S甲_____S乙,S丙_____S丁(填“〉”或“〈”或“=”);
(2)根据小肖、小徐的分割原理,你还能探索出其他的分割方法吗?请在图③中任意给出一种;
(3)由本题的操作过程,你发现了什么规律? Thank you
学科:数学
课型:新授
授课:李祥翠 创设情境,引入新课 1.展示生活中一些平行四边形的实际应用图片,想一想:这里面应用了平行四边形的什么性质?
2.思考:拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?90°什么图形?教学目标:
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.
3.渗透运动联系、从量变到质变的观点.
矩形的定义 有一个角是直角的平行四边形 叫做矩形,通常也叫长方形。定义中的两个条件一个角是直角平行四边形 矩形是我们最常见的图形之一,例如 门窗框、书桌面、教科书封面、地砖等都有矩形形象.想一想矩形是轴对称图形吗?它有几条对称轴? 师生互动,理解新知【探究】在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状. ① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系? 矩形性质1 矩形的四个角都是直角 已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90° A D
B C证明: ∵四边形ABCD是矩形
∴∠A=90° AD∥BC
∴∠A+∠B=180°
∴∠B=90°
∵∠A=∠C ∠B=∠D
∴∠A=∠B=∠C=∠D=90°矩形性质2 矩形的对角线相等已知:四边形ABCD是矩形
求证:AC=BDA D
B C证明: ∵四边形ABCD是矩形
∴∠ABC=∠BCD=90° AB=CD
在 △ABC和 △BCD中
AB=CD
∠ABC=∠DCB
BC=CB
∴△ABC ≌△DCB
∴ AC=BD练一练1. 如图,四边形ABCD是矩形,找出相等的线段和相等的角。 解: 相等的线段有:
AB=CD AD=BC AC=BD
OA=OB=OC=OD
相等的角有:
∠ABC=∠BCD=∠CDA=∠DAB
∠OAB=∠ABO ∠OBC=∠OCB
∠DAO=∠ADO ∠ODC=∠OCD
2. 过矩形ABCD的定点A作对角线BD的垂线,垂足为E,若BE=3.5,ED=10.5,求AB的长。A D
O
B C解: 连接AC交BD于O
∵四边形ABCD是矩形,
∴OB=OD=1/2BD OA=OC=1/2AC
∵AC=BD
∴OA=OB
∵BE=3.5 DE=10.5
∴BD=14
∴OB=OD=7
∴OE=7-3.5=3.5
∴OE=BE
∵AE⊥BD
∴AB=OA
∵OA=OB
∴OA=OB=AB
∴△AOB是等边三角形
∴AB=7OE例1已知:如图,矩形ABCD的两条对角线相交于点O, ∠AOB=60°,AB=4cm。
求矩形对角线的长. 解:∵四边形ABCD是矩形
∴OA=OC= AC
OB=OD= BD
∵AC=BD
∴OA=OB
∵∠AOB=60°
∴△AOB是等边三角形
∴OA=AB=4㎝
∴AC=BD=2OA=8㎝ 在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO=1/2AC=1/2BD.
因此可以得到直角三角形的一个性质: 直角三角形斜边上的中线等于斜边的一半 A D
O
B C练一练 如果矩形的一条对角线长为8cm,两条对角线的一个交角为120度,求矩形的边长。 A D
O
B C解:∵四边形ABCD是矩形,
∴OA=OC=1/2AC OB=OD=1/2BD
∵AC=BD
∴OA=OB
∵∠AOB=180°-120°=60°
∴△AOB是等边三角形
∴∠BAC=60° AB=OA=4㎝
∵∠ABC=90°
∴∠ACB=90°-60°=30°
在Rt△ABC中,根据勾股定理得
BC=4
∴矩形各边的长分别为4 ㎝,4㎝, 4 ㎝,4㎝尝试练习,感受新知1.填空
(1)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为________、________、________、 ________.
(2)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为________cm,________cm,________cm,________cm. 60°120°60°120°5 5 2.选择
(1)下列说法错误的是
(A)矩形的对角线互相平分 (B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形
(2)矩形的对角线把矩形分成的三角形中全等三角形一共有
(A)2对 (B)4对 (C)6对 (D)8对
(3)如图,在矩形ABCD中,AB=3,AD=4,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF=
A. B. C. D.2 CAD3. 已知BD,CE是△ABC的两条高,M,N分别是BC,DE的中点,
求证:(1)EM=DM
(2)MN⊥DE证明:
(1)连接EM DM
∵BD,CE是△ABC的高
∴∠BEC=∠BDC=90°
∵M是BC的中点
∴EM=1/2BC DM=1/2BC
∴EM=DM
(2)∵EM=DM N是ED的中点
∴MN⊥DE 课堂小结,梳理新知这节课我们学习了什么?
大家有哪些收获?深化练习,巩固新知1.矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
(A)12cm (B)10cm (C)7.5cm (D)5cm
2. 在直角三角形ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
3. 矩形是轴对称图形,它有______条对称轴.
4. 在矩形ABCD中,对角线AC,BD相交于点O,若对角线AC=10cm,边BC=8cm,则△ABO的周长为________.
5. 如图1,周长为68的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为( ).
(A)98 (B)196 (C)280 (D)284
6.如图2,根据实际需要,要在矩形实验田里修一条公路(小路任何地方水平宽度都相等),则剩余实验田的面积为________.
7.如图3,在矩形ABCD中,M是BC的中点,且MA⊥MD.若矩形ABCD的周长为48cm,则矩形ABCD的面积为_______图1图2图38. 已知,如图,矩形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OB的中点.
(1)求证:△ADE≌△BCF;
(2)若AD=4cm,AB=8cm,求OF的长.9. 如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边的中点F处,折痕为AE。
求CE的长.10. 已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.
求 AD的长及点A到BD的距离AE的长.A D
E
B C开放练习,拓展新知阅读下列过程:
如图①,小肖过AB,CD的中点画直线EF,把矩形ABCD分割成甲、乙两部分.
如图②,小徐过A,C两点画直线AC,把矩形ABCD分割成丙、丁两部分.
回答下列问题:
(1)填空:S甲_____S乙,S丙_____S丁(填“〉”或“〈”或“=”);
(2)根据小肖、小徐的分割原理,你还能探索出其他的分割方法吗?请在图③中任意给出一种;
(3)由本题的操作过程,你发现了什么规律? Thank you
