第二十二章《二次函数》 单元练习卷(含答案) 2023-2024学年九年级上册数学人教版
文档属性
| 名称 | 第二十二章《二次函数》 单元练习卷(含答案) 2023-2024学年九年级上册数学人教版 | 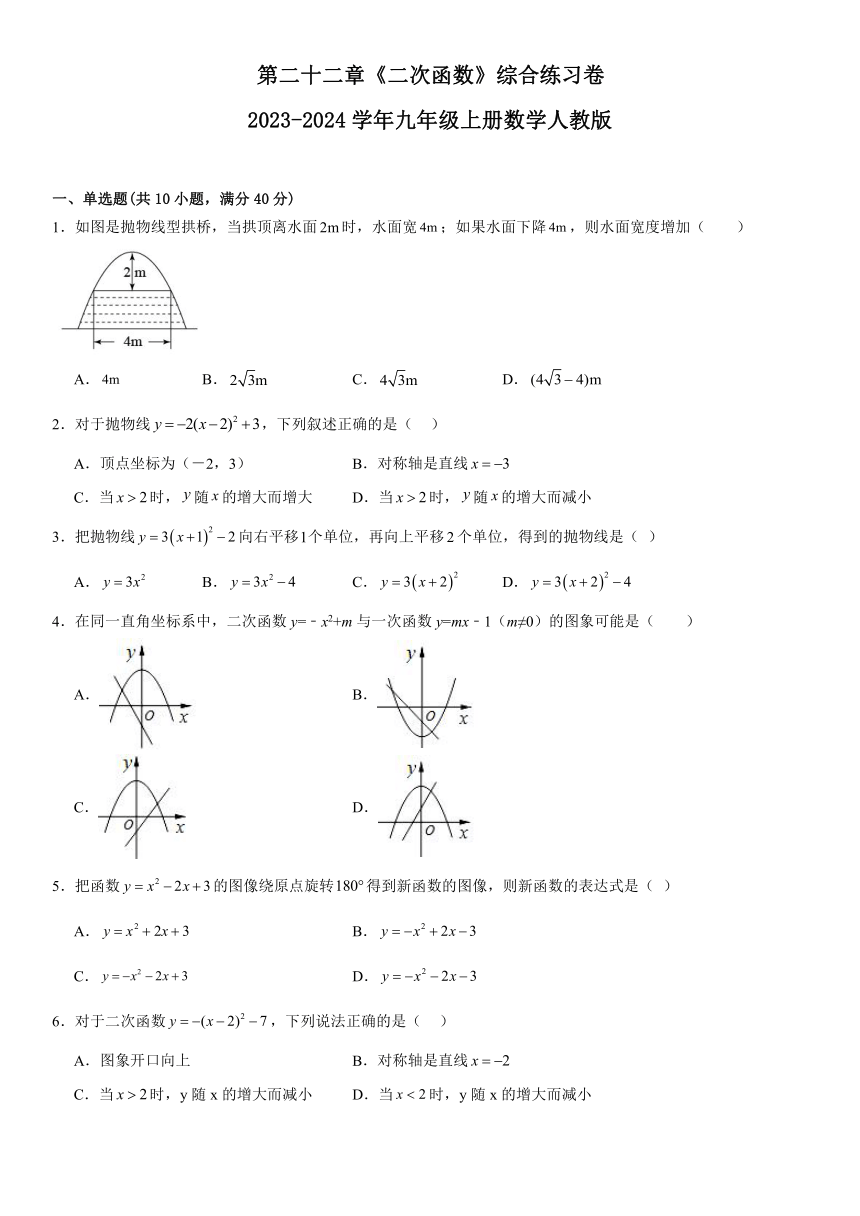 | |
| 格式 | docx | ||
| 文件大小 | 815.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 16:51:50 | ||
图片预览



文档简介
第二十二章《二次函数》综合练习卷
2023-2024学年九年级上册数学人教版
一、单选题(共10小题,满分40分)
1.如图是抛物线型拱桥,当拱顶离水面时,水面宽;如果水面下降,则水面宽度增加( )
A. B. C. D.
2.对于抛物线,下列叙述正确的是( )
A.顶点坐标为(-2,3) B.对称轴是直线
C.当时,随的增大而增大 D.当时,随的增大而减小
3.把抛物线向右平移个单位,再向上平移个单位,得到的抛物线是( )
A. B. C. D.
4.在同一直角坐标系中,二次函数y=﹣x2+m与一次函数y=mx﹣1(m≠0)的图象可能是( )
A. B.
C. D.
5.把函数的图像绕原点旋转得到新函数的图像,则新函数的表达式是( )
A. B.
C. D.
6.对于二次函数,下列说法正确的是( )
A.图象开口向上 B.对称轴是直线
C.当时,y随x的增大而减小 D.当时,y随x的增大而减小
7.矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为 ( )
A. B. C. D.
8.已知,点,,在二次函数图象上,则,,的大小关系是( )
A. B.
C. D.
9.已知y关于x的二次函数表达式是y=ax2+4x-a,下列结论:①若a=-1,函数的最大值是5;②若a=-1,当x≥2时,y随x的增大而减少;③无论a为何值时,函数图象一定经过点(1,-4); ④无论a为何值时,函数图象与x轴有两个交点,其中正确的是( )
A.①② B.①②④ C.①②③ D.②③④
10.二次函数的图象如图所示,下列说法①a>0;②b>0;③c<0;④,正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(共8小题,满分32分)
11.将抛物线先沿轴向右平移2个单位长度,再向上平移3个单位长度后得到新的抛物线,那么新抛物线的表达式为 .
12.已知二次函数中的x和y满足下表:
x … 0 1 2 3 …
y … 10 5 2 1 2 …
根据图表中信息推断,方程的根为 .
13.已知二次函数上有两点和,且,则 .(填“>”“<”或“=”).
14.已知抛物线过点、,则a的取值范围是 .
15.点,,在抛物线上,则,,的大小关系是 (用“<”号连接).
16.抛物线上部分点的横坐标与纵坐标的对应值如表:
x … 0 2 4 …
y … m n m 1 0 …
由表可知,抛物线与x轴的一个交点的坐标是(4,0),则抛物线与x轴的另一个交点的坐标是 .
17.二次函数中的几组对应值如下表.
-2 1 5
m n p
表中m、n、p的大小关系为 (用“<”连接)
18.已知y=x2+(1﹣a)x+2是关于x的二次函数,当x的取值范围是0≤x≤4时,y仅在x=4时取得最大值,则实数a的取值范围是 .
三、解答题(共6小题,每题8分,满分48分)
19.我们可以用表示为自变量的函数,如一次函数,可表示,,.
(1)已知二次函数;
①求证:不论为何值,此函数图像与轴总有两个交点;
②若,是否存在实数,使得当时,函数的最小值为,若存在,求出的值,若不存在,请说明理由;
(2)已知函数,,若实数、使得,求的值.
20.小明将小球沿地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度()与它的飞行时间()满足二次函数关系,与的几组对应值如下表所示:
() …
() …
(1)求关于的函数解析式(不要求写的取值范围)
(2)问:小球的飞行高度能否达到?请说明理由
21.如图,印刷一张矩形的包装纸,印刷部分的长为8cm,宽为4cm,上下空白宽各cm,左右空白宽各xcm,四周空白处的面积为Scm2.
(1)求S与x的关系式;
(2)当四周空白处的面积为18cm2时,求x的值.
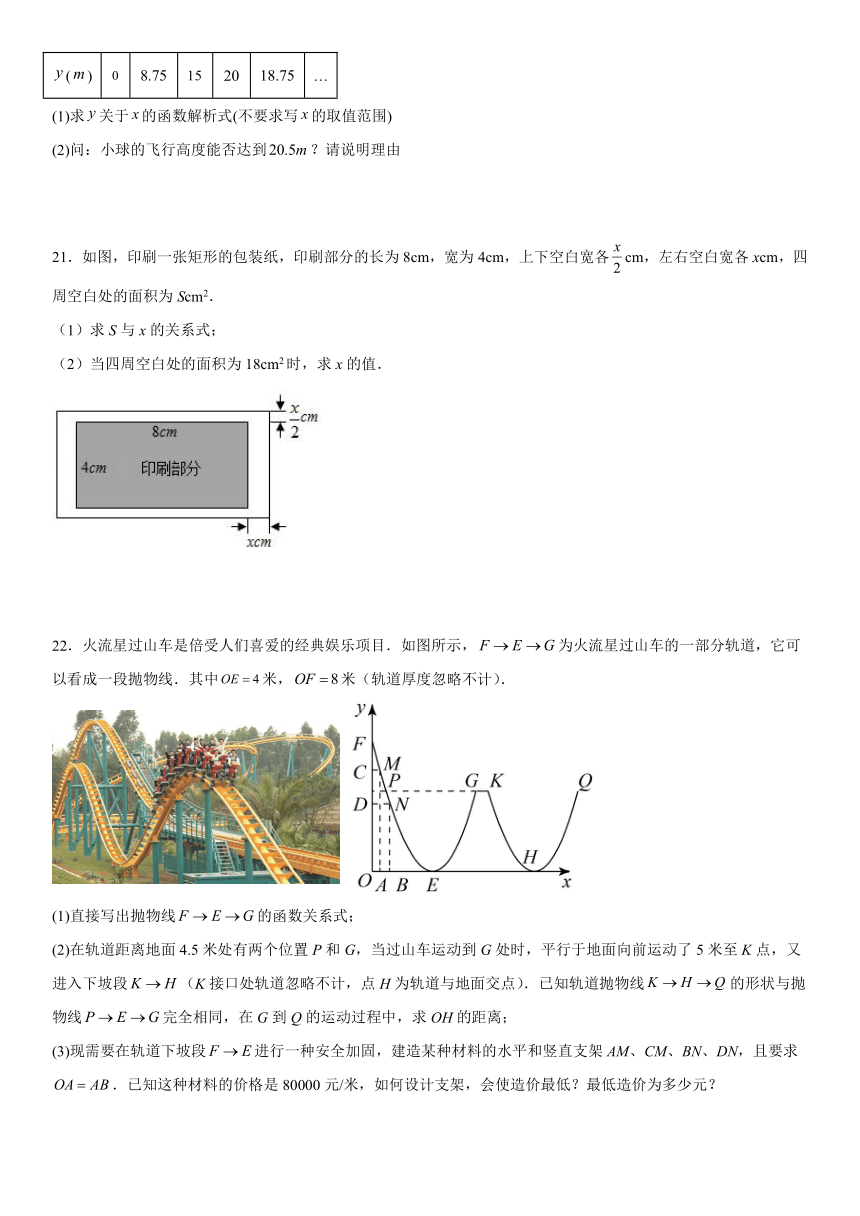
22.火流星过山车是倍受人们喜爱的经典娱乐项目.如图所示,为火流星过山车的一部分轨道,它可以看成一段抛物线.其中米,米(轨道厚度忽略不计).
(1)直接写出抛物线的函数关系式;
(2)在轨道距离地面4.5米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运动了5米至K点,又进入下坡段(K接口处轨道忽略不计,点H为轨道与地面交点).已知轨道抛物线的形状与抛物线完全相同,在G到Q的运动过程中,求OH的距离;
(3)现需要在轨道下坡段进行一种安全加固,建造某种材料的水平和竖直支架AM、CM、BN、DN,且要求.已知这种材料的价格是80000元/米,如何设计支架,会使造价最低?最低造价为多少元?
23.如图甲,抛物线y=ax2+bx–1经过A(–1,0),B(2,0)两点,交y轴于点C(0,–1).
(1)求抛物线的表达式和直线BC的表达式.
(2)如图乙,点P为在第四象限内抛物线上的一个动点,过点P作x轴的垂线PE交直线BC于点D.
①在点P运动过程中,四边形ACPB的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
②是否存在点P使得以点O,C,D为顶点的三角形是等腰三角形?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
24.如图,抛物线与x轴交于点,B两点,与y轴交于点,抛物线的顶点在直线上.
(1)求抛物线的解析式;
(2)点P为第一象限内抛物线上的一个动点,过点P作轴交BC于点Q,求线段PQ长度的最大值,及此时点P的坐标;
(3)点M在x轴上,点N在抛物线的对称轴上,若以点M,N,C,B为顶点的四边形是平行四边形,请直接写出点M的坐标.
参考答案:
1.D
2.D
3.A
4.C
5.D
6.C
7.A
8.D
9.B
10.B
11.或
12.或5
13.<
14.或
15.y2<y3<y1
16.
17.n<m<p
18.a<5
19.(1)①证明略;②存在,或;(2).
20.(1)y=-5x2+20x;(2)不能,理由见解析
21.(1)S=2x2+16x;(2)所以当四周空白处的面积为18cm2时,x的值为1
22.(1)抛物线的函数关系式为
(2)OH的距离为米
(3)当时,造价最低,最低造价为元.
23.(1),;(2)①存在,最大值为2;②存在,P坐标为
或(1,–1)或.
24.(1);(2)PQ长度的最大值为,点P的坐标为;(3)点M的坐标为,,.
2023-2024学年九年级上册数学人教版
一、单选题(共10小题,满分40分)
1.如图是抛物线型拱桥,当拱顶离水面时,水面宽;如果水面下降,则水面宽度增加( )
A. B. C. D.
2.对于抛物线,下列叙述正确的是( )
A.顶点坐标为(-2,3) B.对称轴是直线
C.当时,随的增大而增大 D.当时,随的增大而减小
3.把抛物线向右平移个单位,再向上平移个单位,得到的抛物线是( )
A. B. C. D.
4.在同一直角坐标系中,二次函数y=﹣x2+m与一次函数y=mx﹣1(m≠0)的图象可能是( )
A. B.
C. D.
5.把函数的图像绕原点旋转得到新函数的图像,则新函数的表达式是( )
A. B.
C. D.
6.对于二次函数,下列说法正确的是( )
A.图象开口向上 B.对称轴是直线
C.当时,y随x的增大而减小 D.当时,y随x的增大而减小
7.矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为 ( )
A. B. C. D.
8.已知,点,,在二次函数图象上,则,,的大小关系是( )
A. B.
C. D.
9.已知y关于x的二次函数表达式是y=ax2+4x-a,下列结论:①若a=-1,函数的最大值是5;②若a=-1,当x≥2时,y随x的增大而减少;③无论a为何值时,函数图象一定经过点(1,-4); ④无论a为何值时,函数图象与x轴有两个交点,其中正确的是( )
A.①② B.①②④ C.①②③ D.②③④
10.二次函数的图象如图所示,下列说法①a>0;②b>0;③c<0;④,正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(共8小题,满分32分)
11.将抛物线先沿轴向右平移2个单位长度,再向上平移3个单位长度后得到新的抛物线,那么新抛物线的表达式为 .
12.已知二次函数中的x和y满足下表:
x … 0 1 2 3 …
y … 10 5 2 1 2 …
根据图表中信息推断,方程的根为 .
13.已知二次函数上有两点和,且,则 .(填“>”“<”或“=”).
14.已知抛物线过点、,则a的取值范围是 .
15.点,,在抛物线上,则,,的大小关系是 (用“<”号连接).
16.抛物线上部分点的横坐标与纵坐标的对应值如表:
x … 0 2 4 …
y … m n m 1 0 …
由表可知,抛物线与x轴的一个交点的坐标是(4,0),则抛物线与x轴的另一个交点的坐标是 .
17.二次函数中的几组对应值如下表.
-2 1 5
m n p
表中m、n、p的大小关系为 (用“<”连接)
18.已知y=x2+(1﹣a)x+2是关于x的二次函数,当x的取值范围是0≤x≤4时,y仅在x=4时取得最大值,则实数a的取值范围是 .
三、解答题(共6小题,每题8分,满分48分)
19.我们可以用表示为自变量的函数,如一次函数,可表示,,.
(1)已知二次函数;
①求证:不论为何值,此函数图像与轴总有两个交点;
②若,是否存在实数,使得当时,函数的最小值为,若存在,求出的值,若不存在,请说明理由;
(2)已知函数,,若实数、使得,求的值.
20.小明将小球沿地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度()与它的飞行时间()满足二次函数关系,与的几组对应值如下表所示:
() …
() …
(1)求关于的函数解析式(不要求写的取值范围)
(2)问:小球的飞行高度能否达到?请说明理由
21.如图,印刷一张矩形的包装纸,印刷部分的长为8cm,宽为4cm,上下空白宽各cm,左右空白宽各xcm,四周空白处的面积为Scm2.
(1)求S与x的关系式;
(2)当四周空白处的面积为18cm2时,求x的值.
22.火流星过山车是倍受人们喜爱的经典娱乐项目.如图所示,为火流星过山车的一部分轨道,它可以看成一段抛物线.其中米,米(轨道厚度忽略不计).
(1)直接写出抛物线的函数关系式;
(2)在轨道距离地面4.5米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运动了5米至K点,又进入下坡段(K接口处轨道忽略不计,点H为轨道与地面交点).已知轨道抛物线的形状与抛物线完全相同,在G到Q的运动过程中,求OH的距离;
(3)现需要在轨道下坡段进行一种安全加固,建造某种材料的水平和竖直支架AM、CM、BN、DN,且要求.已知这种材料的价格是80000元/米,如何设计支架,会使造价最低?最低造价为多少元?
23.如图甲,抛物线y=ax2+bx–1经过A(–1,0),B(2,0)两点,交y轴于点C(0,–1).
(1)求抛物线的表达式和直线BC的表达式.
(2)如图乙,点P为在第四象限内抛物线上的一个动点,过点P作x轴的垂线PE交直线BC于点D.
①在点P运动过程中,四边形ACPB的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
②是否存在点P使得以点O,C,D为顶点的三角形是等腰三角形?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
24.如图,抛物线与x轴交于点,B两点,与y轴交于点,抛物线的顶点在直线上.
(1)求抛物线的解析式;
(2)点P为第一象限内抛物线上的一个动点,过点P作轴交BC于点Q,求线段PQ长度的最大值,及此时点P的坐标;
(3)点M在x轴上,点N在抛物线的对称轴上,若以点M,N,C,B为顶点的四边形是平行四边形,请直接写出点M的坐标.
参考答案:
1.D
2.D
3.A
4.C
5.D
6.C
7.A
8.D
9.B
10.B
11.或
12.或5
13.<
14.或
15.y2<y3<y1
16.
17.n<m<p
18.a<5
19.(1)①证明略;②存在,或;(2).
20.(1)y=-5x2+20x;(2)不能,理由见解析
21.(1)S=2x2+16x;(2)所以当四周空白处的面积为18cm2时,x的值为1
22.(1)抛物线的函数关系式为
(2)OH的距离为米
(3)当时,造价最低,最低造价为元.
23.(1),;(2)①存在,最大值为2;②存在,P坐标为
或(1,–1)或.
24.(1);(2)PQ长度的最大值为,点P的坐标为;(3)点M的坐标为,,.
同课章节目录
