2.2 整式的加减 学案(含答案)—初中数学人教版七年级上册
文档属性
| 名称 | 2.2 整式的加减 学案(含答案)—初中数学人教版七年级上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 00:00:00 | ||
图片预览




文档简介
第6讲 整式的加减
知识点1 合并同类项
根据乘法分配律把同类项合并成一项叫做合并同类项.
【典例】
例1若7axb2与﹣3a3by的和为单项式,则xy= 9 .
【解答】解:∵7axb2与﹣3a3by的和为单项式,
∴x=3,y=2,
∴xy=32=9.
故答案为:9.
【方法总结】
此题主要考查了合并同类项,正确掌握相关运算法则是解题关键.
例2计算3a2bc﹣4a2bc的结果是( )
A.a2bc B.﹣a2bc C.7a2bc D.﹣1
【解答】解:3a2bc﹣4a2bc=﹣a2bc,
故选:B.
【方法总结】
此题考查合并同类项,关键是根据合并同类项的法则计算.
例3计算3a2bc﹣4a2bc的结果是( )
A.a2bc B.﹣a2bc C.7a2b c D.﹣1
【解答】解:3a2bc﹣4a2bc
=﹣a2bc.
故选:B.
【方法总结】
此题考查合并同类项,关键是根据合并同类项的法则计算.
【随堂练习】
1.计算2x2﹣3x2+x2的结果等于 0 .
【解答】解:2x2﹣3x2+x2
=(2﹣3+1)x2
=0.
故答案为:0.
2.计算a2﹣3a2+4a2的结果等于 2a2 .
【解答】解:a2﹣3a2+4a2
=(1﹣3+4)a2
=2a2.
故答案为:2a2.
3.若单项式xm﹣1y2与单项式﹣x2021yn+1可以合并,则m﹣n= 2021 .
【解答】解:∵单项式xm﹣1y2与单项式﹣x2021yn+1可以合并,
∴xm﹣1y2与﹣x2021yn+1是同类项,
∴m﹣1=2021,n+1=2,
∴m=2022,n=1,
∴m﹣n=2022﹣1=2021.
故答案为:2021.
知识点2 去括号与添括号
1.去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里面各项的符号都不改变.
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里面各项的符号都要改变.
2.添括号法则:
添括号时,如果括号前面是加号,括到括号里的各项都不变符号;如果括号前面是减号,括到括号里的各项都改变符号.
【典例】
例1下列运算结果正确的是( )
A.2x+3y=5xy B.7a2b﹣4ab2=3a2b
C.x﹣(3y﹣2)=x﹣3y﹣2 D.﹣2(x+y)=﹣2x﹣2y
【解答】解:A、2x与3y不是同类项,不能合并,不符合题意.
B、7a2b与4ab2=不是同类项,不能合并,不符合题意.
C、x﹣(3y﹣2)=x﹣3y+2,不符合题意.
D、原式=﹣2x﹣2y,符合题意.
故选:D.
【方法总结】
本题主要考查了合并同类项和去括号,去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘,再运用括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“﹣”,去括号后,括号里的各项都改变符号.
例2去括号:9﹣(2)= 92 .
【解答】解:原式=92.
故答案是:92.
【方法总结】
本题主要考查了去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
【随堂练习】
1.下列去括号正确的是( )
A.a﹣(2b﹣c)=a﹣2b﹣c B.a+2(2b﹣3c)=a﹣4b﹣6c
C.a+(b﹣3c)=a﹣b+3c D.a﹣3(2b﹣3c)=a﹣6b+9c
【解答】解:A、a﹣(2b﹣c)=a﹣2b+c,故本选项错误;
B、a+2(2b﹣3c)=a+4b﹣6c,故本选项错误;
C、a+(b﹣3c)=a+b﹣3c,故本选项错误;
D、a﹣3(2b﹣3c)=a﹣6b+9c,故本选项正确;
故选:D.
2.下列去括号的过程
(1)a+(b﹣c)=a+b﹣c;(2)a﹣(b+c)=a﹣b﹣c;(3)a﹣(b﹣c)=a﹣b﹣c;(4)a﹣(b﹣c)=a﹣b+c.
其中,运算结果正确的个数为( )
A.1 B.2 C.3 D.4
【解答】解:(1)a+(b﹣c)=a+b﹣c,故此题正确;
(2)a﹣(b+c)=a﹣b﹣c,故此题正确;
(3)a﹣(b﹣c)=a﹣b+c,故此题错误;
(4)a﹣(b﹣c)=a﹣b+c,故此题正确.
所以运算结果正确的个数为3个,
故选:C.
3.﹣2(x2+x﹣2)= ﹣2x2﹣2x+4 .
【解答】解:﹣2(x2+x﹣2)
=﹣(2x2+2x﹣4)
=﹣2x2﹣2x+4.
故答案为:﹣2x2﹣2x+4.
4.去括号:﹣3(a+3b)= ﹣3a﹣9b .
【解答】解:﹣3(a+3b)
=﹣3a﹣9b.
故答案为:﹣3a﹣9b.
知识点3:整式的加减
几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接。然后去括号,再合并同类项.
【典例】
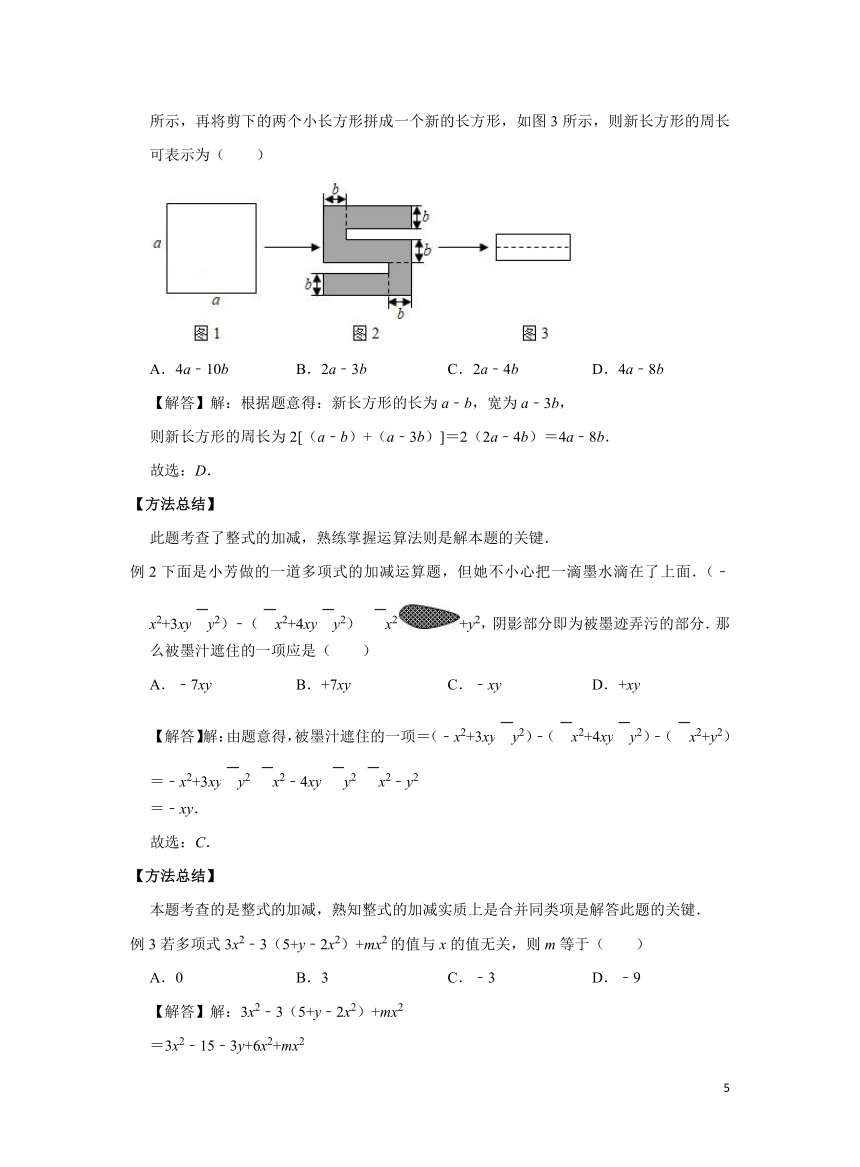
例1如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“S”图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为( )
A.4a﹣10b B.2a﹣3b C.2a﹣4b D.4a﹣8b
【解答】解:根据题意得:新长方形的长为a﹣b,宽为a﹣3b,
则新长方形的周长为2[(a﹣b)+(a﹣3b)]=2(2a﹣4b)=4a﹣8b.
故选:D.
【方法总结】
此题考查了整式的加减,熟练掌握运算法则是解本题的关键.
例2下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.(﹣x2+3xyy2)﹣(x2+4xyy2)x2+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
A.﹣7xy B.+7xy C.﹣xy D.+xy
【解答】解:由题意得,被墨汁遮住的一项=(﹣x2+3xyy2)﹣(x2+4xyy2)﹣(x2+y2)
=﹣x2+3xyy2x2﹣4xyy2x2﹣y2
=﹣xy.
故选:C.
【方法总结】
本题考查的是整式的加减,熟知整式的加减实质上是合并同类项是解答此题的关键.
例3若多项式3x2﹣3(5+y﹣2x2)+mx2的值与x的值无关,则m等于( )
A.0 B.3 C.﹣3 D.﹣9
【解答】解:3x2﹣3(5+y﹣2x2)+mx2
=3x2﹣15﹣3y+6x2+mx2
=(9+m)x2﹣3y﹣15,
∵多项式3x2﹣3(5+y﹣2x2)+mx2的值与x的值无关,
∴9+m=0,
解得m=﹣9,
故选:D.
【方法总结】
本题考查整式的加减,解答本题的关键是明确整式加减的计算方法.
【随堂练习】
1.将两边长分别为a和b(a>b)的正方形纸片按图1、图2两种方式置于长方形ABCD中,(图1、图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1上中阴影部分的周长为C1,图2中阴部分的周长为C2,则C1﹣C2的值( )
A.0 B.a﹣b C.2a﹣2b D.2b﹣2a
【解答】解:由题意知:C1=AD+CD﹣b+AD﹣a+a﹣b+a+AB﹣a,
因为四边形ABCD是长方形,
所以AB=CD
∴C1=AD+CD﹣b+AD﹣a+a﹣b+a+AB﹣a=2AD+2AB﹣2b,
同理,C2=AD﹣b+AB﹣a+a﹣b+a+BC﹣a+AB=2AD+2AB﹣2b,
故C1﹣C2=0.
故选:A.
2.如果M=x2+3x+12,N=﹣x2+3x﹣5,那么M与N的大小关系是( )
A.M>N B.M<N C.M=N D.无法确定
【解答】解:∵M=x2+3x+12,N=﹣x2+3x﹣5,
∴M﹣N
=(x2+3x+12)﹣(﹣x2+3x﹣5)
=x2+3x+12+x2﹣3x+5
=2x2+17,
∵不论x为何值,2x2≥0,
∴M﹣N>0,
∴M>N,
故选:A.
3.以下是马小虎同学化简代数式(a2b+4ab)﹣3(ab﹣a2b)的过程.
(a2b+4ab)﹣3(ab﹣a2b)
=a2b+4ab﹣3ab﹣3a2b…第一步,
=a2b﹣3a2b+4ab﹣3ab …第二步,
=ab﹣2a2b …第三步,
(1)马小虎同学解答过程在第 一 步开始出错,出错原因是 去掉括号时,没有变号 .
(2)请你帮助马小虎同学写出正确的解答过程.
【解答】解:(1)马小虎同学解答过程在第一步开始出错,出错原因是去掉括号时,没有变号,
故答案为:一,去掉括号时,没有变号;
(2)正确的解答过程是:
(a2b+4ab)﹣3(ab﹣a2b)
=a2b+4ab﹣3ab+3a2b
=4a2b+ab.
4.化简:
(1)3(2a﹣b)﹣4(3b﹣a)+2(a﹣b);
(2)3x2+(2x2﹣3x)﹣(5x2﹣x).
【解答】解:(1)原式=6a﹣3b﹣12b+4a+2a﹣2b
=12a﹣17b;
(2)原式=3x2+2x2﹣3x﹣5x2+x
=﹣2x.
知识点4:化简求值
给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.
【典例】
例1解答下列问题:先化简,再求值:(18a﹣3a2)﹣5(1+2a+a2),其中a2﹣a+3=0.
【解答】解:(18a﹣3a2)﹣5(1+2a+a2),
=18a﹣3a2﹣5﹣10a﹣5a2,
=﹣8a2+8a﹣5,
∵a2﹣a+3=0,
∴a2﹣a=﹣3,
∴﹣8a2+8a﹣5,
=﹣8(a2﹣a)﹣5,
=﹣8×(﹣3)﹣5,
=24﹣5,
=19.
【方法总结】
本题考查了整式的化简求值,正确地去括号、合并同类项使化简的结果中出现a2﹣a,是解决本题的关键.
例2阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b),“整体思想”是中学教学课题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
(1)尝试应用:把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣5(a﹣b)2+7(a﹣b)2的结果是 5(a﹣b)2 .
(2)已知x2﹣2y=1,求3x2﹣6y﹣5的值.
(3)拓展探索:
已知a﹣2b=2,2b﹣c=﹣5,c﹣d=9,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
【解答】解:(1)3(a﹣b)2﹣5(a﹣b)2+7(a﹣b)2=(3﹣5+7)(a﹣b)2=5(a﹣b)2.
故答案为:5(a﹣b)2;
(2)3x2﹣6y﹣5=3(x2﹣2y)﹣5,
把x2﹣2y=1代入上式,
原式=3×1﹣5=﹣2;
(3)(a﹣c)+(2b﹣d)﹣(2b﹣c)
=a﹣c+2b﹣d﹣2b+c
=(a﹣2b)+(c﹣d)+(2b﹣c),
把a﹣2b=2,2b﹣c=﹣5,c﹣d=9代入上式,
原式=2+9﹣5=6.
【方法总结】
本题主要考查了整式的加减﹣化简求值,熟练掌握整式的加减运算法则进行计算是解决本题的关键.
【随堂练习】
1.先化简,再求值:﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x,y.
【解答】解:原式=﹣6x2+3xy+4x2+4xy﹣24
=﹣2x2+7xy﹣24,
当x,y时,原式=﹣2×()2+7×()24=﹣25.
2.先化简,再求值:﹣(a2+6ab﹣1)+2(b+3ab),其中a,b.
【解答】解:原式=﹣a2﹣6ab+1+2b+6ab﹣1
=﹣a2+2b,
当a,b时,
原式=﹣()2+21×4.
3.先化简,再求值:2(x2﹣2y2)﹣(x﹣2y)﹣(x﹣3y2+2x2),其中x=﹣3,y=﹣2.
【解答】解:原式=2x2﹣4y2﹣x+2y﹣x+3y2﹣2x2
=﹣y2﹣2x+2y;
当x=﹣3,y=﹣2时,
原式=﹣(﹣2)2﹣2×(﹣3)+2×(﹣2)
=﹣4+6﹣4
=﹣2.
4.先化简,再求值:2x2y﹣2[6xy﹣2(4xy﹣2)﹣2x2y]+8,其中x,y=2.
【解答】解:原式=2x2y﹣2(6xy﹣8xy+4﹣2x2y)+8
=2x2y﹣12xy+16xy﹣8+4x2y+8
=6x2y+4xy,
当时,原式=62+4×()×2=﹣1.
综合运用
1.下列运算结果正确的是( )
A.2x+3y=5xy B.﹣2(x+y)=﹣2x﹣2y
C.x﹣(3y﹣2)=x﹣3y﹣2 D.7a2b﹣4ab2=3a2b
【解答】解:A、2x与3y不是同类项,不能合并,不符合题意;
B、根据去括号法则,括号前面是负号时,去掉括号后,里面的符号都要改变,﹣2(x+y)=﹣2x﹣2y,符合题意;
C、根据去括号法则,括号前面是负号时,去掉括号后,里面的符号都要改变,x﹣(3y﹣2)=x﹣3y+2,不符合题意;
D、7a2b和4ab2不是同类项,不能合并,不符合题意;
故选:B.
2.下列计算正确的是( )
A.a+(﹣b+c﹣3d)=a﹣b+c﹣3d
B.a﹣(﹣2b+c﹣d)=a+2b﹣c﹣d
C.a﹣2(﹣2b+4c﹣3d)=a+4b+8c﹣6d
D.a﹣2(﹣3b+c﹣7d)=a+6b﹣c+7d
【解答】解:A、a+(﹣b+c﹣3d)=a﹣b+c﹣3d,符合题意;
B、a﹣(﹣2b+c﹣d)=a+2b﹣c+d,不符合题意;
C、a﹣2(﹣2b+4c﹣3d)=a+4b﹣8c+6d,不符合题意;
D、a﹣2(﹣3b+c﹣7d)=a+6b﹣2c+14d,不符合题意.
故选:A.
3.下列单项式中,可以与x2y3合并同类项的是( )
A.x3y2 B. C.3x2y D.2x2y3z
【解答】解:A、x3y2与x2y3,所含字母相同,但是相同字母的指数不相同,不是同类项,所以不能合并,故本选项不合题意;
B、与x2y3,所含字母相同,相同字母的指数相同,是同类项,能合并,故本选项符合题意;
C、x2y与x2y3,所含字母相同,但是相同字母的指数不相同,不是同类项,所以不能合并,故本选项不合题意;
D、2x2y3z与x2y3,所含字母不尽相同,不是同类项,所以不能合并,故本选项不合题意;
故选:B.
4.已知两个单项式3xym与﹣3xny2的和为0,则m+n的值是 3 .
【解答】解:∵两个单项式3xym与﹣3xny2的和为0,
∴两个单项式是同类项,
即m=2,n=1,
∴m+n=3.
故答案为:3.
5.一个多项式加上﹣2a+6等于2a2+a+3,则这个多项式是 2a2+3a﹣3 .
【解答】解:∵一个多项式加上﹣2a+6等于2a2+a+3,
∴这个多项式是:2a2+a+3﹣(﹣2a+6)
=2a2+a+3+2a﹣6
=2a2+3a﹣3.
故答案为:2a2+3a﹣3.
6.化简下列各式:
(1)2(ab﹣2c)+(﹣ab+2c);
(2)﹣2(3x2﹣xy)+3(x2﹣xy+2).
【解答】解:(1)原式=2ab﹣4c﹣ab+2c=ab﹣2c;
(2)原式=﹣6x2+2xy+3x2﹣3xy+6=﹣3x2﹣xy+6.
7.已知:A=5x2+4x+1,B=x2+3x﹣2.
(1)求2A+B;
(2)求A﹣2B.
【解答】解:(1)∵A=5x2+4x+1,B=x2+3x﹣2,
∴2A+B=2(5x2+4x+1)+(x2+3x﹣2)
=10x2+8x+2+x2+3x﹣2
=11x2+11x;
(2)∵A=5x2+4x+1,B=x2+3x﹣2,
∴A﹣2B=(5x2+4x+1)﹣2(x2+3x﹣2)
=5x2+4x+1﹣2x2﹣6x+4
=3x2﹣2x+5.
8.先化简,再求值:(3a2b﹣ab2)﹣2(ab2﹣3a2b),其中a,b=﹣3.
【解答】解:原式=3a2b﹣ab2﹣2ab2+6a2b
=9a2b﹣3ab2,
当a,b=﹣3时,
原式=9×()2×(﹣3)﹣3(﹣3)2
=9(﹣3)﹣9
=﹣3﹣9
=﹣12.
9.先化简,再求值:5a2b﹣2(a2b﹣2ab2+1)+3(﹣2ab2+a2b),其中a=﹣2,b=1.
【解答】解:原式=5a2b﹣2a2b+4ab2﹣2﹣6ab2+3a2b
=6a2b﹣2ab2﹣2
=2ab(3a﹣b)﹣2,
把a=﹣2,b=1代入上式,
原式=2×(﹣2)×1×[3×(﹣2)﹣1]﹣2=26.
1
知识点1 合并同类项
根据乘法分配律把同类项合并成一项叫做合并同类项.
【典例】
例1若7axb2与﹣3a3by的和为单项式,则xy= 9 .
【解答】解:∵7axb2与﹣3a3by的和为单项式,
∴x=3,y=2,
∴xy=32=9.
故答案为:9.
【方法总结】
此题主要考查了合并同类项,正确掌握相关运算法则是解题关键.
例2计算3a2bc﹣4a2bc的结果是( )
A.a2bc B.﹣a2bc C.7a2bc D.﹣1
【解答】解:3a2bc﹣4a2bc=﹣a2bc,
故选:B.
【方法总结】
此题考查合并同类项,关键是根据合并同类项的法则计算.
例3计算3a2bc﹣4a2bc的结果是( )
A.a2bc B.﹣a2bc C.7a2b c D.﹣1
【解答】解:3a2bc﹣4a2bc
=﹣a2bc.
故选:B.
【方法总结】
此题考查合并同类项,关键是根据合并同类项的法则计算.
【随堂练习】
1.计算2x2﹣3x2+x2的结果等于 0 .
【解答】解:2x2﹣3x2+x2
=(2﹣3+1)x2
=0.
故答案为:0.
2.计算a2﹣3a2+4a2的结果等于 2a2 .
【解答】解:a2﹣3a2+4a2
=(1﹣3+4)a2
=2a2.
故答案为:2a2.
3.若单项式xm﹣1y2与单项式﹣x2021yn+1可以合并,则m﹣n= 2021 .
【解答】解:∵单项式xm﹣1y2与单项式﹣x2021yn+1可以合并,
∴xm﹣1y2与﹣x2021yn+1是同类项,
∴m﹣1=2021,n+1=2,
∴m=2022,n=1,
∴m﹣n=2022﹣1=2021.
故答案为:2021.
知识点2 去括号与添括号
1.去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里面各项的符号都不改变.
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里面各项的符号都要改变.
2.添括号法则:
添括号时,如果括号前面是加号,括到括号里的各项都不变符号;如果括号前面是减号,括到括号里的各项都改变符号.
【典例】
例1下列运算结果正确的是( )
A.2x+3y=5xy B.7a2b﹣4ab2=3a2b
C.x﹣(3y﹣2)=x﹣3y﹣2 D.﹣2(x+y)=﹣2x﹣2y
【解答】解:A、2x与3y不是同类项,不能合并,不符合题意.
B、7a2b与4ab2=不是同类项,不能合并,不符合题意.
C、x﹣(3y﹣2)=x﹣3y+2,不符合题意.
D、原式=﹣2x﹣2y,符合题意.
故选:D.
【方法总结】
本题主要考查了合并同类项和去括号,去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘,再运用括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“﹣”,去括号后,括号里的各项都改变符号.
例2去括号:9﹣(2)= 92 .
【解答】解:原式=92.
故答案是:92.
【方法总结】
本题主要考查了去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
【随堂练习】
1.下列去括号正确的是( )
A.a﹣(2b﹣c)=a﹣2b﹣c B.a+2(2b﹣3c)=a﹣4b﹣6c
C.a+(b﹣3c)=a﹣b+3c D.a﹣3(2b﹣3c)=a﹣6b+9c
【解答】解:A、a﹣(2b﹣c)=a﹣2b+c,故本选项错误;
B、a+2(2b﹣3c)=a+4b﹣6c,故本选项错误;
C、a+(b﹣3c)=a+b﹣3c,故本选项错误;
D、a﹣3(2b﹣3c)=a﹣6b+9c,故本选项正确;
故选:D.
2.下列去括号的过程
(1)a+(b﹣c)=a+b﹣c;(2)a﹣(b+c)=a﹣b﹣c;(3)a﹣(b﹣c)=a﹣b﹣c;(4)a﹣(b﹣c)=a﹣b+c.
其中,运算结果正确的个数为( )
A.1 B.2 C.3 D.4
【解答】解:(1)a+(b﹣c)=a+b﹣c,故此题正确;
(2)a﹣(b+c)=a﹣b﹣c,故此题正确;
(3)a﹣(b﹣c)=a﹣b+c,故此题错误;
(4)a﹣(b﹣c)=a﹣b+c,故此题正确.
所以运算结果正确的个数为3个,
故选:C.
3.﹣2(x2+x﹣2)= ﹣2x2﹣2x+4 .
【解答】解:﹣2(x2+x﹣2)
=﹣(2x2+2x﹣4)
=﹣2x2﹣2x+4.
故答案为:﹣2x2﹣2x+4.
4.去括号:﹣3(a+3b)= ﹣3a﹣9b .
【解答】解:﹣3(a+3b)
=﹣3a﹣9b.
故答案为:﹣3a﹣9b.
知识点3:整式的加减
几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接。然后去括号,再合并同类项.
【典例】
例1如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“S”图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为( )
A.4a﹣10b B.2a﹣3b C.2a﹣4b D.4a﹣8b
【解答】解:根据题意得:新长方形的长为a﹣b,宽为a﹣3b,
则新长方形的周长为2[(a﹣b)+(a﹣3b)]=2(2a﹣4b)=4a﹣8b.
故选:D.
【方法总结】
此题考查了整式的加减,熟练掌握运算法则是解本题的关键.
例2下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.(﹣x2+3xyy2)﹣(x2+4xyy2)x2+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
A.﹣7xy B.+7xy C.﹣xy D.+xy
【解答】解:由题意得,被墨汁遮住的一项=(﹣x2+3xyy2)﹣(x2+4xyy2)﹣(x2+y2)
=﹣x2+3xyy2x2﹣4xyy2x2﹣y2
=﹣xy.
故选:C.
【方法总结】
本题考查的是整式的加减,熟知整式的加减实质上是合并同类项是解答此题的关键.
例3若多项式3x2﹣3(5+y﹣2x2)+mx2的值与x的值无关,则m等于( )
A.0 B.3 C.﹣3 D.﹣9
【解答】解:3x2﹣3(5+y﹣2x2)+mx2
=3x2﹣15﹣3y+6x2+mx2
=(9+m)x2﹣3y﹣15,
∵多项式3x2﹣3(5+y﹣2x2)+mx2的值与x的值无关,
∴9+m=0,
解得m=﹣9,
故选:D.
【方法总结】
本题考查整式的加减,解答本题的关键是明确整式加减的计算方法.
【随堂练习】
1.将两边长分别为a和b(a>b)的正方形纸片按图1、图2两种方式置于长方形ABCD中,(图1、图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1上中阴影部分的周长为C1,图2中阴部分的周长为C2,则C1﹣C2的值( )
A.0 B.a﹣b C.2a﹣2b D.2b﹣2a
【解答】解:由题意知:C1=AD+CD﹣b+AD﹣a+a﹣b+a+AB﹣a,
因为四边形ABCD是长方形,
所以AB=CD
∴C1=AD+CD﹣b+AD﹣a+a﹣b+a+AB﹣a=2AD+2AB﹣2b,
同理,C2=AD﹣b+AB﹣a+a﹣b+a+BC﹣a+AB=2AD+2AB﹣2b,
故C1﹣C2=0.
故选:A.
2.如果M=x2+3x+12,N=﹣x2+3x﹣5,那么M与N的大小关系是( )
A.M>N B.M<N C.M=N D.无法确定
【解答】解:∵M=x2+3x+12,N=﹣x2+3x﹣5,
∴M﹣N
=(x2+3x+12)﹣(﹣x2+3x﹣5)
=x2+3x+12+x2﹣3x+5
=2x2+17,
∵不论x为何值,2x2≥0,
∴M﹣N>0,
∴M>N,
故选:A.
3.以下是马小虎同学化简代数式(a2b+4ab)﹣3(ab﹣a2b)的过程.
(a2b+4ab)﹣3(ab﹣a2b)
=a2b+4ab﹣3ab﹣3a2b…第一步,
=a2b﹣3a2b+4ab﹣3ab …第二步,
=ab﹣2a2b …第三步,
(1)马小虎同学解答过程在第 一 步开始出错,出错原因是 去掉括号时,没有变号 .
(2)请你帮助马小虎同学写出正确的解答过程.
【解答】解:(1)马小虎同学解答过程在第一步开始出错,出错原因是去掉括号时,没有变号,
故答案为:一,去掉括号时,没有变号;
(2)正确的解答过程是:
(a2b+4ab)﹣3(ab﹣a2b)
=a2b+4ab﹣3ab+3a2b
=4a2b+ab.
4.化简:
(1)3(2a﹣b)﹣4(3b﹣a)+2(a﹣b);
(2)3x2+(2x2﹣3x)﹣(5x2﹣x).
【解答】解:(1)原式=6a﹣3b﹣12b+4a+2a﹣2b
=12a﹣17b;
(2)原式=3x2+2x2﹣3x﹣5x2+x
=﹣2x.
知识点4:化简求值
给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.
【典例】
例1解答下列问题:先化简,再求值:(18a﹣3a2)﹣5(1+2a+a2),其中a2﹣a+3=0.
【解答】解:(18a﹣3a2)﹣5(1+2a+a2),
=18a﹣3a2﹣5﹣10a﹣5a2,
=﹣8a2+8a﹣5,
∵a2﹣a+3=0,
∴a2﹣a=﹣3,
∴﹣8a2+8a﹣5,
=﹣8(a2﹣a)﹣5,
=﹣8×(﹣3)﹣5,
=24﹣5,
=19.
【方法总结】
本题考查了整式的化简求值,正确地去括号、合并同类项使化简的结果中出现a2﹣a,是解决本题的关键.
例2阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b),“整体思想”是中学教学课题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
(1)尝试应用:把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣5(a﹣b)2+7(a﹣b)2的结果是 5(a﹣b)2 .
(2)已知x2﹣2y=1,求3x2﹣6y﹣5的值.
(3)拓展探索:
已知a﹣2b=2,2b﹣c=﹣5,c﹣d=9,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
【解答】解:(1)3(a﹣b)2﹣5(a﹣b)2+7(a﹣b)2=(3﹣5+7)(a﹣b)2=5(a﹣b)2.
故答案为:5(a﹣b)2;
(2)3x2﹣6y﹣5=3(x2﹣2y)﹣5,
把x2﹣2y=1代入上式,
原式=3×1﹣5=﹣2;
(3)(a﹣c)+(2b﹣d)﹣(2b﹣c)
=a﹣c+2b﹣d﹣2b+c
=(a﹣2b)+(c﹣d)+(2b﹣c),
把a﹣2b=2,2b﹣c=﹣5,c﹣d=9代入上式,
原式=2+9﹣5=6.
【方法总结】
本题主要考查了整式的加减﹣化简求值,熟练掌握整式的加减运算法则进行计算是解决本题的关键.
【随堂练习】
1.先化简,再求值:﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x,y.
【解答】解:原式=﹣6x2+3xy+4x2+4xy﹣24
=﹣2x2+7xy﹣24,
当x,y时,原式=﹣2×()2+7×()24=﹣25.
2.先化简,再求值:﹣(a2+6ab﹣1)+2(b+3ab),其中a,b.
【解答】解:原式=﹣a2﹣6ab+1+2b+6ab﹣1
=﹣a2+2b,
当a,b时,
原式=﹣()2+21×4.
3.先化简,再求值:2(x2﹣2y2)﹣(x﹣2y)﹣(x﹣3y2+2x2),其中x=﹣3,y=﹣2.
【解答】解:原式=2x2﹣4y2﹣x+2y﹣x+3y2﹣2x2
=﹣y2﹣2x+2y;
当x=﹣3,y=﹣2时,
原式=﹣(﹣2)2﹣2×(﹣3)+2×(﹣2)
=﹣4+6﹣4
=﹣2.
4.先化简,再求值:2x2y﹣2[6xy﹣2(4xy﹣2)﹣2x2y]+8,其中x,y=2.
【解答】解:原式=2x2y﹣2(6xy﹣8xy+4﹣2x2y)+8
=2x2y﹣12xy+16xy﹣8+4x2y+8
=6x2y+4xy,
当时,原式=62+4×()×2=﹣1.
综合运用
1.下列运算结果正确的是( )
A.2x+3y=5xy B.﹣2(x+y)=﹣2x﹣2y
C.x﹣(3y﹣2)=x﹣3y﹣2 D.7a2b﹣4ab2=3a2b
【解答】解:A、2x与3y不是同类项,不能合并,不符合题意;
B、根据去括号法则,括号前面是负号时,去掉括号后,里面的符号都要改变,﹣2(x+y)=﹣2x﹣2y,符合题意;
C、根据去括号法则,括号前面是负号时,去掉括号后,里面的符号都要改变,x﹣(3y﹣2)=x﹣3y+2,不符合题意;
D、7a2b和4ab2不是同类项,不能合并,不符合题意;
故选:B.
2.下列计算正确的是( )
A.a+(﹣b+c﹣3d)=a﹣b+c﹣3d
B.a﹣(﹣2b+c﹣d)=a+2b﹣c﹣d
C.a﹣2(﹣2b+4c﹣3d)=a+4b+8c﹣6d
D.a﹣2(﹣3b+c﹣7d)=a+6b﹣c+7d
【解答】解:A、a+(﹣b+c﹣3d)=a﹣b+c﹣3d,符合题意;
B、a﹣(﹣2b+c﹣d)=a+2b﹣c+d,不符合题意;
C、a﹣2(﹣2b+4c﹣3d)=a+4b﹣8c+6d,不符合题意;
D、a﹣2(﹣3b+c﹣7d)=a+6b﹣2c+14d,不符合题意.
故选:A.
3.下列单项式中,可以与x2y3合并同类项的是( )
A.x3y2 B. C.3x2y D.2x2y3z
【解答】解:A、x3y2与x2y3,所含字母相同,但是相同字母的指数不相同,不是同类项,所以不能合并,故本选项不合题意;
B、与x2y3,所含字母相同,相同字母的指数相同,是同类项,能合并,故本选项符合题意;
C、x2y与x2y3,所含字母相同,但是相同字母的指数不相同,不是同类项,所以不能合并,故本选项不合题意;
D、2x2y3z与x2y3,所含字母不尽相同,不是同类项,所以不能合并,故本选项不合题意;
故选:B.
4.已知两个单项式3xym与﹣3xny2的和为0,则m+n的值是 3 .
【解答】解:∵两个单项式3xym与﹣3xny2的和为0,
∴两个单项式是同类项,
即m=2,n=1,
∴m+n=3.
故答案为:3.
5.一个多项式加上﹣2a+6等于2a2+a+3,则这个多项式是 2a2+3a﹣3 .
【解答】解:∵一个多项式加上﹣2a+6等于2a2+a+3,
∴这个多项式是:2a2+a+3﹣(﹣2a+6)
=2a2+a+3+2a﹣6
=2a2+3a﹣3.
故答案为:2a2+3a﹣3.
6.化简下列各式:
(1)2(ab﹣2c)+(﹣ab+2c);
(2)﹣2(3x2﹣xy)+3(x2﹣xy+2).
【解答】解:(1)原式=2ab﹣4c﹣ab+2c=ab﹣2c;
(2)原式=﹣6x2+2xy+3x2﹣3xy+6=﹣3x2﹣xy+6.
7.已知:A=5x2+4x+1,B=x2+3x﹣2.
(1)求2A+B;
(2)求A﹣2B.
【解答】解:(1)∵A=5x2+4x+1,B=x2+3x﹣2,
∴2A+B=2(5x2+4x+1)+(x2+3x﹣2)
=10x2+8x+2+x2+3x﹣2
=11x2+11x;
(2)∵A=5x2+4x+1,B=x2+3x﹣2,
∴A﹣2B=(5x2+4x+1)﹣2(x2+3x﹣2)
=5x2+4x+1﹣2x2﹣6x+4
=3x2﹣2x+5.
8.先化简,再求值:(3a2b﹣ab2)﹣2(ab2﹣3a2b),其中a,b=﹣3.
【解答】解:原式=3a2b﹣ab2﹣2ab2+6a2b
=9a2b﹣3ab2,
当a,b=﹣3时,
原式=9×()2×(﹣3)﹣3(﹣3)2
=9(﹣3)﹣9
=﹣3﹣9
=﹣12.
9.先化简,再求值:5a2b﹣2(a2b﹣2ab2+1)+3(﹣2ab2+a2b),其中a=﹣2,b=1.
【解答】解:原式=5a2b﹣2a2b+4ab2﹣2﹣6ab2+3a2b
=6a2b﹣2ab2﹣2
=2ab(3a﹣b)﹣2,
把a=﹣2,b=1代入上式,
原式=2×(﹣2)×1×[3×(﹣2)﹣1]﹣2=26.
1
