第11章 三角形(含解析)2023-2024学年 人教版八年级上册数学新题速解
文档属性
| 名称 | 第11章 三角形(含解析)2023-2024学年 人教版八年级上册数学新题速解 |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 17:50:49 | ||
图片预览




文档简介
2023年秋季学期人教版八年级数学新题速解:第11章--三角形
一、单选题
1.(2023秋·黑龙江齐齐哈尔·八年级校联考阶段练习)如图,在中,,,、的平分线相交于,过点作,交于,交于,那么下列结论正确的是( )
①;②;③;④.
A.①② B.③④ C.①③ D.①②④
2.(2023秋·安徽阜阳·八年级统考阶段练习)如图,把三角形纸片沿折叠,当点落在三角形内部时,与,之间的数量关系是( )
A. B.
C. D.
3.(2023秋·浙江绍兴·八年级校联考阶段练习)如图,在中,已知分别是边的中点,且阴影部分图形的面积为7,则的面积为( )
A.14 B.21 C.28 D.32
4.(2023秋·山东临沂·八年级临沂第九中学校考阶段练习)如图,是边的中线,点E在上,,的面积是3,则的面积是( )
A.4 B.3 C.2 D.1
5.(2023秋·浙江绍兴·八年级校联考阶段练习)已知的三个内角满足,则这个三角形是( )
A.钝角三角形 B.直角三角形 C.任意三角形 D.锐角三角形
6.(2023秋·安徽阜阳·八年级统考阶段练习)如图,在中,,,是上一点,若为直角三角形,则的度数为( )
A. B. C.或 D.或
7.(2023秋·广东东莞·八年级东莞市东华初级中学校考阶段练习)如图,中,于点D,则下列结论不一定成立的是( )
A. B. C. D.
8.(2023秋·湖北十堰·八年级校联考阶段练习)如图,点D,E分别在上,连接.若于D,,则的大小为()
A. B. C. D.
9.(2023秋·陕西延安·八年级统考阶段练习)若一个多边形从一个顶点出发可引4条对角线,则这个多边形对角线的总数为( )
A.14 B.28 C.24 D.20
10.(2023秋·山东临沂·八年级临沂第九中学校考阶段练习)如图,已知是的边上的中线,若,,的周长比的周长多2,则的长为( )
A.14 B.12 C.10 D.8
11.(2023秋·湖北武汉·八年级校考阶段练习)如图,在中,、分别是高和角平分线,点在的延长线上,交于,交于,下列结论:①;②;③;④,正确的个数是( )
A.1 B.2 C.3 D.4
12.(2023秋·广东广州·八年级校考阶段练习)如图1,线段、相交于点O,连接、,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,和的平分线和相交于点P,并且与、分别相交于M、N.其中正确的结论是( )
(1)在图1中;(2)在图2中“8 字形”的个数为 4;(3)图2中,当度,度时,度;(4)图2中和为任意角时其他条件不变.
A.(1)(2)(3) B.(1)(2)(4) C.(1)(3)(4) D.(1)(2)(3)(4)
13.(2023秋·山东日照·八年级校考阶段练习)多边形的内角和增加180°,则它的边数( )
A.增加1 B.增加2 C.增加3 D.不变
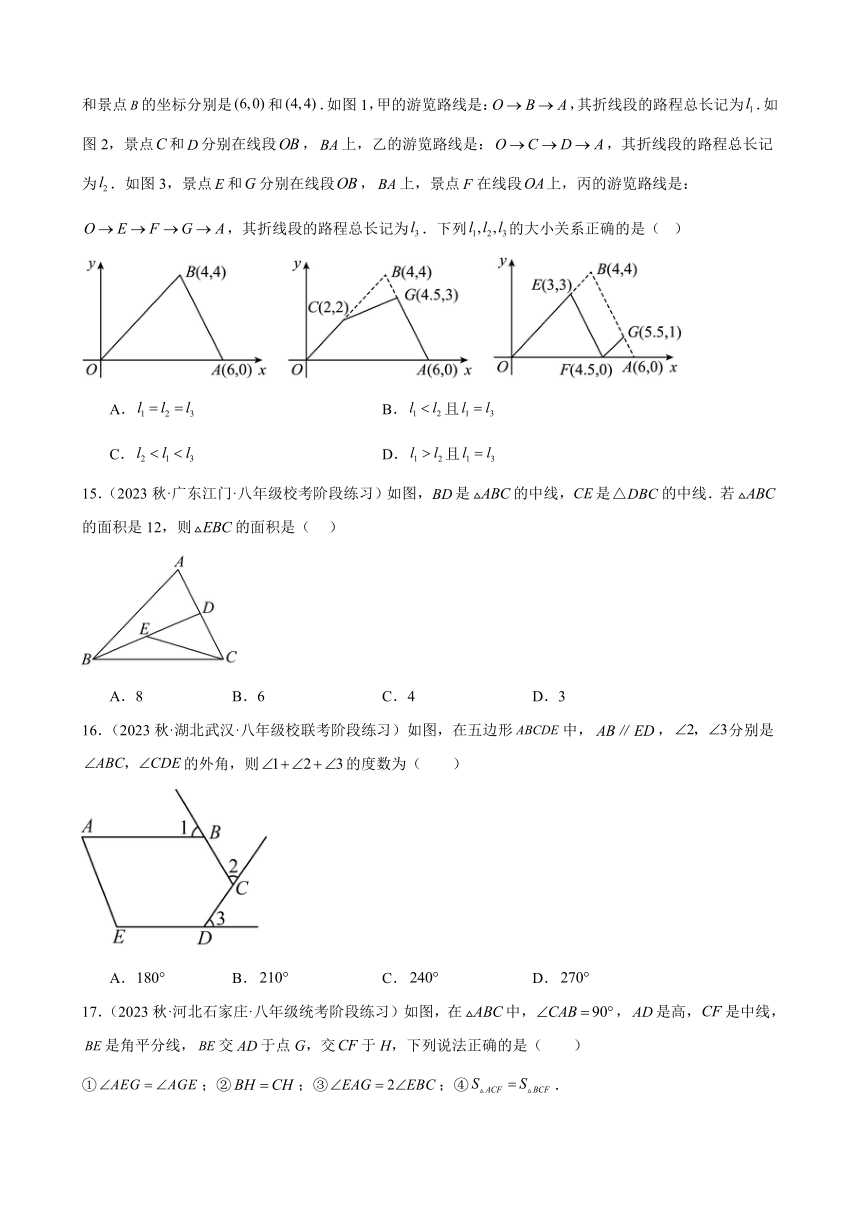
14.(2023秋·安徽淮南·八年级校联考阶段练习)以某公园西门为原点建立平面直角坐标系,东门
和景点的坐标分别是和.如图1,甲的游览路线是:,其折线段的路程总长记为.如图2,景点和分别在线段,上,乙的游览路线是:,其折线段的路程总长记为.如图3,景点和分别在线段,上,景点在线段上,丙的游览路线是:,其折线段的路程总长记为.下列的大小关系正确的是( )
A. B.且
C. D.且
15.(2023秋·广东江门·八年级校考阶段练习)如图,是的中线,是的中线.若的面积是12,则的面积是( )
A.8 B.6 C.4 D.3
16.(2023秋·湖北武汉·八年级校联考阶段练习)如图,在五边形中,,分别是的外角,则的度数为( )
A. B. C. D.
17.(2023秋·河北石家庄·八年级统考阶段练习)如图,在中,,是高,是中线,是角平分线,交于点G,交于H,下列说法正确的是( )
①;②;③;④.
A.①③ B.①②③ C.①③④ D.②③④
18.(2023秋·陕西延安·八年级校联考阶段练习)如图,,分别是的角平分线和高,若,,则的度数为( )
A. B. C. D.
19.(2023秋·天津静海·八年级校考阶段练习)如图,在中,,和的平分线相交于点G,则的度数为( )
A. B. C. D.
20.(2023秋·黑龙江齐齐哈尔·八年级统考阶段练习)如图,在中,,,、的平分线相交于,过点作,交于,交于,那么下列结论正确的是( )
①;②;③;④.
A.①② B.③④ C.①③ D.①②③
二、填空题
21.(2023秋·湖北武汉·八年级校联考阶段练习)如图,点G为的三条中线的交点,,若
,则面积的最大值是 .
22.(2023秋·陕西延安·八年级统考阶段练习)如图,处在处的南偏西方向,处在处的南偏东方向,处在处的北偏东方向,则的度数为 .
23.(2023秋·湖北随州·八年级校考阶段练习)如图,,分别是,的中点,若,则 .
24.(2023秋·山东临沂·八年级临沂第九中学校考阶段练习)如图,在中,,点D、E分别是,上一点,将沿折叠,使点A落在点F处,已知,的度数 .
25.(2023秋·安徽阜阳·八年级统考阶段练习)如图,和是的两个外角,若,则的度数为 .
26.(2023秋·陕西延安·八年级统考阶段练习)如图,正六边形和正五边形的边
重合,的延长线与交于点,则的度数是 .
27.(2023秋·广东东莞·八年级东莞市东华初级中学校考阶段练习)在中,若,则 .
28.(2023秋·湖北黄冈·八年级校联考阶段练习)如图,是的角平分线,,垂足为,连接.若,,则的度数为 .
29.(2023秋·全国·八年级专题练习)如图,在中,,和的平分线交于点,得;和的平分线交于点,得;…;和的平分线交于点,则 °.
30.(2023秋·内蒙古呼和浩特·八年级校考阶段练习)如图,是的角平分线,D是边上一点,交于点F,若,,则的度数为 .
三、解答题
31.(2023秋·陕西商洛·八年级校考阶段练习)如图,是的角平分线,过点作交的延长线于点,点在边上,连接交于点.
若,求证:;(2)若,求的度数.
32.(2023秋·辽宁大连·八年级统考阶段练习)(1)如图,的外角和的平分线交于点F.用等式表示与的数量关系;
(2)如图,的平分线和的外角的平分线交于点H.用等式表示与的数量关系,并证明.
33.(2023秋·辽宁大连·八年级校联考阶段练习)如图,在四边形中,,平分,平分.求证.
34.(2023秋·安徽阜阳·八年级统考阶段练习)如图,在中,与外角的角平分线相交于点.
(1)当,时,求的度数;(2)求证:.
35.(2023秋·安徽阜阳·八年级统考阶段练习)如图,在中,是的中线,是的中线.
(1)若,求的长;(2)若的周长为,,且与的周长差为,求的长.
36.(2023秋·广东东莞·八年级东莞市东华初级中学校考阶段练习)在中,平分交于点D,
(1)求的度数;
(2)如图①,若于点F,交于点E.求的度数.
(3)如图②,若平分交于点E,交于点F,求的度数.
37.(2023秋·安徽阜阳·八年级统考阶段练习)如图1,线段,相交于点,连接,,我们把形如图的图形称为“字形”.
(1)求证:;
(2)如图2,求的度数;
(3)如图3,平分,平分的邻补角,试猜想,与之间的数量关系,并说明理由.
38.(2023秋·安徽阜阳·八年级统考阶段练习)如图,与分别是的角平分线和高.
(1)已知,,求度数;
(2)探究:小明认为如果只知道,也能得出的度数,你认为可能吗?若能,请你写出求解过程;若不能,请说明理由.
39.(2023秋·河北沧州·八年级校考阶段练习)如果一个角是另一个角的2倍,那么称是的“二倍角”.例如:,,则是的“二倍角”.已知在中,.
(1)若是的“二倍角”,则______;
(2)若的三个内角中,有一个角是另一个角的“二倍角”,则______;
(3)如图1,作的外角平分线,过点作的平行线.
①求证:是的“二倍角”;
②如图2,再作的角平分线,求证:是的“二倍角”.
40.(2023秋·全国·八年级专题练习)在中,BD平分交于点,点是线段上的动点(不与点重合),过点作交射线于点,的平分线所在直线与射线交于点.
(1)如图,点在线段上运动.
①若,则的度数是 ;的度数是 ,
②探究与之间的数量关系,并说明理由;
(2)若点在线段上运动时,请直接写出与之间的数量关系.
参考答案:
1.C
【分析】根据三角形内角和定理对进行判断;根据角平分线的定义和三角形内角和定理可得到,则可对进行判断;根据平行线的性质对进行判断;先根据角平分线的性质得到,然后根据平行线的性质对进行判断.
【详解】解:,,
∴,所以正确;
、的平分线相交于,
∴,,
∴,所以错误;
∵,
∴,所以正确;
平分,
∴,
∵,
∴,所以错误;
综上分析可知,①③正确.
故选:C.
【点睛】本题考查了平行线的性质,三角形的内角和定理的应用,角平分线的定义,掌握以上基础知识是解本题的关键.
2.A
【分析】首先根据折叠性质可得,,利用邻补角可得,,在中,根据三角形内角和定理可得,整理即可得出结果.
【详解】解:如图
三角形纸片沿折叠,当点落在三角形内部,
,,
,,
,,
在中,,
,
整理得:,
故选:.
【点睛】本题考查了三角形内角和定理,折叠性质,邻补角定义,熟练掌握三角形内角和定理是解答本题的关键.
3.C
【分析】由是的中点可得,由是的中点可得,,从而得到,再由即可得到答案.
【详解】解:是的中点,
,
是的中点,
,,
,
,
,
故选:C.
【点睛】本题考查了与中线有关的三角形面积的计算,利用题中所给的条件,将面积进行转化是解此题的关键.
4.D
【分析】利用三角形面积公式,等高的三角形的面积比等于底边的比,由此利用已知条件可以分别求出.
【详解】解:∵是边的中线,的面积是3,
∴,
∵,
∴,
故选:D.
【点睛】本题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半;三角形的中线将三角形分成面积相等的两部分.
5.B
【分析】设,,,根据三角形内角和定理可得,求出的值即可得到答案.
【详解】解:的三个内角满足,
设,,,
,
,
解得:,
,
这个三角形是直角三角形,
故选:B.
【点睛】本题考查了三角形内角和定理,熟练掌握三角形内角和为是解题的关键.
6.C
【分析】利用三角形内角和先求出的度数,再根据点的位置不同分情况利用求出的度数,进而求出的度数.
【详解】解:在中,,,
,
如图,当时,
,
,
,
当时,
.
故选:.
【点睛】本题考查了三角形内角和定理,熟练掌握三角形内角和定理是解答本题的关键.
7.B
【分析】根据直角三角形的性质可得,再由,可得,再根据等角的余角相等可得,,即可求解.
【详解】解:∵,
∴,故A选项不符合题意;
∵,
∴,
∴,故选项C不符合题意;
又∵,
∴,
∴不一定成立,故B选项符合题意;
∵,,
∴,故D选项不符合题意;
故选:B.
【点睛】本题考查直角三角形的性质、余角的性质,利用直角三角形的性质和等角的余角相等得出,,是解题的关键.
8.D
【分析】由三角形的内角和定理和平角定义,可得由此解答即可.
【详解】解:∵
,,
,
,
,
,
故选:D.
【点睛】本题考查了三角形内角和定理和三角形外角性质,掌握这些知识点是解题的关键.
9.A
【分析】根据一个边形从一个顶点出发有条对角线,即可求出该多边形的边数.再根据边形对角线的总数为,即可求解.
【详解】解:根据题意,一个多边形从一个顶点出发可引4条对角线,
可知该多边形的边数为,
∴这个多边形对角线的总数为.
故选:A.
【点睛】本题主要考查了多边形的对角线的条数问题,熟练掌握边形的相关公式是解题关键.
10.C
【分析】依据 是 的边 上的中线,可得 ,再根据 的周长比 的周长多 2 , 即可得到 的长;
【详解】解:∵ 是 的边 上的中线,
又 ∵ 的周长比 的周长多2 ,
即 ,
故选 :C.
【点睛】本题考查了三角形的中线, 求出两个三角形的周长的差等于两边的差是解题的关键.
11.C
【分析】①根据,,以及即可推出;②根据角平分线的定义和三角形外角的性质证明即可;③证明,由①知:即可证明
;④由同角的余角相等证明,再根据三角形外角的性质及角平分线的性质即可推出,即可判断.
【详解】解:∵,
∴.
∵,
∴.
∵,
∴.
故①正确;
∵平分,
∴.
∵,
∴.
∵,
∴.
故②正确;
∵平分,
∴.
∵,
∴.
∴.
由①知:,
∴.
故③正确;
∵,
∴.
∴.
∵平分,
∴,
∴.
∴
故④错误;
综上可知,正确的有①②③,共3个,
故选C.
【点睛】本题主要考查了三角形的内角和定理,三角形外角的性质,同角的余角相等等知识,正确运用三角形的高、角平分线的概念以及三角形的内角和定理是解题的关键.
12.C
【分析】根据对顶角相等可得,再根据三角形的内角和定理即可判断(1)正确;根据“8字形”的定义即可判断(2)错误;如图(见解析),根据角平分线的定义可得,再根据结论(1)可得,,两式相加即可判断(4)正确;将度,度代入结论(4)计算即可判断(3)正确.
【详解】解:,,
,则结论(1)正确;
在图2中,线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
在图2中“8 字形”共有6个,则结论(2)错误;
如图,和的平分线和相交于点,
,
同结论(1)可知,,,
两式相加得:,
,则结论(4)正确;
则当度,度时,,
解得度,则结论(3)正确;
综上,正确的结论是(1)(3)(4),
故选:C.
【点睛】本题考查了三角形的内角和定理、角平分线的定义等知识点,掌握理解“8 字形”的定义是解题关键.
13.A
【分析】根据多边形的内角和公式,可知多边形的内角和是的整数倍,可得多边形的内角和增加180°,它就增加1条边.
【详解】∵多边形的内角和是,
∴多边形的内角和增加180°,它的边数就增加1.
故选:A.
【点睛】本题主要考查了多边形内角和与边数的关系,解决问题的关键是熟练掌握多边形的内角和公式.
14.D
【分析】根据三角形三边的关系即可证明,根据平移的性质可证明.
【详解】解:根据题意可得,,
∴;
将线段平移,可得到线段,线段移可得到线段,
∴,,
,
∴,
故选:D.
【点睛】本题考查了三角形三边关系,平移的性质,题目新颖,灵活运用所学知识是解题的关键.
15.D
【分析】根据的面积是12,三角形中线将三角形面积两等分,即可求解.
【详解】解:∵是的中线,
∴,
∵是的中线,
∴,
故选:D.
【点睛】本题考查三角形的中线及三角形面积公式,掌握三角形的中线将三角形面积两等分是解题的关键.
16.A
【分析】如图,反向延长,根据平行线的性质可得,再结合多边形外角和定理即可求解.
【详解】解:反向延长,
∵,
∴,
根据多边形的外角和定理可得,
∴.
故选A.
【点睛】本题考查多边形外角和问题,平行线的性质,解题的关键是掌握多边形外角和为360度.
17.C
【分析】根据三角形内角和定理求出,根据三角形的外角性质即可推出①;根据等腰三角形的判定判断②即可;根据三角形内角和定理求出,根据角平分线定义即可判断③;根据等底等高的三角形的面积相等即可判断④.
【详解】解:∵是角平分线,
∴,
∵为高,
∴,
∵,
∴,
∴,
故①正确;
根据已知条件不能推出,即不能推出,
故②错误;
∵为高,
∴,
∵,
∴,
∴,
∵是角平分线,
∴,
∴,
即,
故③正确;
∵是中线,
∴,
∴(等底等高的三角形的面积相等),
故④正确.
故选:C.
【点睛】本题考查了三角形内角和定理,三角形的外角性质,三角形的角平分线、中线、高,等腰三角形的判定等知识点,能综合运用定理进行推理是解此题的关键.
18.B
【分析】利用三角形内角和定理求出,再根据角平分线和高线,可求出和,进而可求出的度数.
【详解】解:,,
,
是的角平分线,
,
又是的高,
,
,
.
故选:B.
【点睛】本题考查了三角形的内角和定理、角平分线的性质等知识点,解题的关键是掌握三角形的内角和定理.
19.D
【分析】先利用角平分线的性质和三角形的内角和定理求出与和的度数,再利用三角形的外角和内角的关系得结论.
【详解】解:、分别是和的平分线,
,.
,,
.
,
,
.
故选:D.
【点睛】本题主要考查了三角形的内角和定理及推论,掌握“三角形的内角和是”、“三角形的外角等于与它不相邻的两个内角的和”及角平分线的定义是解决本题的关键.
20.C
【分析】根据三角形内角和定理对进行判断;根据角平分线的定义和三角形内角和定理可得到,则可对进行判断;根据平行线的性质对进行判断;先根据角平分线的性质得到,然后根据平行线的性质对进行判断.
【详解】解:,,
∴,所以正确;
、的平分线相交于,
∴,所以错误;
∵,
∴,所以正确;
平分,
∴,
∵,
∴,所以错误;
综上分析可知,①②③正确.
故选:C.
【点睛】本题考查了等腰三角形的判定与性质:平行线的性质,等腰三角形提供了好多相等的线段和相等的角,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.
21.4
【分析】由三角形的面积关系可证,即可求解.
【详解】解:点为的三条中线的交点,
,是的中线,
,,,即,
,
,
,
,
,
当时,面积有最大值,
∵,
面积的最大值,
故答案为4
【点睛】本题考查了三角形的中线与面积的关系,理解题意是解题的关键.
22./度
【分析】根据平行线的性质,可得内错角相等,根据角的和差,可得、,根据三角形的内角和公式,可得答案.
【详解】解:如图,
根据方向角的定义,可得.
∵,
∴.
∵是正南正北方向,
∴,
又∵,
∴,
.
故答案为:
【点睛】本题主要考查了方向角的定义,平行线的性质以及三角形的内角和定理,正确理解定义是解题的关键.
23.4
【分析】三角形的中线将三角形分成面积相等的两部分,据此可得,.
【详解】解:∵点是的中点,
∴,
∵点是的中点,
∴.
故答案为:4.
【点睛】本题主要考查了三角形中线有关的面积计算,解题关键是理解并掌握三角形中线的定义和性质.
24.
【分析】由折叠可知:,由三角形的内角和定理可求,即可求得,再利用三角形的内角和定理可求,进而可求解.
【详解】解:由折叠可知:,
∵,
∴,
∴,
∵,
∴,
∴.
故答案为:
【点睛】本题主要考查三角形的内角和定理,翻折问题,掌握三角形的内角和定理是解题的关键.
25./234度
【分析】根据三角形的外角的性质和三角形的内角和定理即可得到结论.
【详解】解:和是的两个外角,
,
,
.
故答案为:.
【点睛】本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形外角的性质是解答此题的关键.
26./84度
【分析】利用多边形的内角和与正多边形的性质分别求得的度数,然后利用等边对等角及三角形内角和定理求得的度数,再结合四边形的内角和为进行计算即可.
【详解】解:∵六边形为正六边形,
∴,
∵五边形为正五边形,
∴,
∴,
∵四边形的内角和为,
∴,
故答案为:.
【点睛】本题主要考查多边形的内角和及正多边形的性质,结合已知条件求得的度数是解题的关键.
27./75度
【分析】由:,,,可得出,求得,最后求得.
【详解】解:,,
又,
,
,
.
故答案为:.
【点睛】本题考查了三角形内角和定理,牢记“三角形内角和是”是解题的关键.
28./28度
【分析】在中,利用三角形内角和定理,可求出的度数,由平分,利用角平分线的定义,可求出的度数,在中,利用三角形内角和定理,可求出的度数,再结合,即可求出的度数.
【详解】解:在中,,,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴.
故答案为:.
【点睛】本题主要考查了三角形内角和定理以及角平分线的定义,牢记“三角形内角和是
”是解题的关键.
29./
【分析】根据角平分线的性质和三角形外角性质得出和的关系,进而求出与的关系,找出规律,得到与的关系即可求解.
【详解】解:和的平分线交于点,
,
,
同理,,
,
,
当时,,
(度)
故答案为:.
【点睛】本题考查了三角形外角性质与角平分线的定义,找出规律是解题的关键.
30./79度
【分析】角平分线得到,根据已知条件得到,得到,根据三角形的内角和定理,得到,求出的度数,再根据三角形的内角和定理以及对顶角相等,即可得出结果.
【详解】解:如图,
∵是的角平分线,
∴,
∵,,
∴,
∴,
∵,
∴,
∴;
故答案为:.
【点睛】本题考查与角平分线有关的三角形的内角和问题.熟练掌握角平分线平分角,以及三角形的内角和为,是解题的关键.
31.(1)见解析
(2)
【分析】(1)先根据垂直等于得到,则,再证明,加上,则,然后根据平行线的判定方法得到结论;
(2)先根据三角形内角和定理可计算出,则,根据三角形内角和定理得到,即,从而可求出的度数.
【详解】(1)证明:,
,
,
是的角平分线,
,
,
即,
,
,
;
(2)解:,,
,
,
,
,
即,
.
【点睛】本题考查了三角形内角和定理、平行线额判定,解题的关键是运用三角形内角和定理可根据两已知角求第三个角.
32.(1);(2).见解析
【分析】(1)利用角平分线的性质和三角形的外角性质可求出,再利用三角形内角和定理即可求出的度数.
(2)先根据三角形的外角性质得到,再根据角平分线的定义解答即可.
【详解】解:(1)∵为两外角的平分线,
∴;
由三角形内角和定理得:
(2)
证明:∵的外角的平分线和的平分线交于点H,
∴.
∵,
∴.
∴
∴.
【点睛】本题考查三角形的内角和定理,三角形外角的性质,角平分线的定义,熟练掌握三角形的内角和定理以及三角形外角的性质是解题的关键.
33.见解析
【分析】根据四边形的内角和得到,根据角平分线的定义得到,则,再因为在中,,根据余角的性质即可得出结论.
【详解】证明:∵在四边形中,,,
∴.
∵平分,平分,
∴,
∴
∵在中,,
∴.
【点睛】本题主要考查多边形的内角和外角,角平分线的定义,余角的性质,熟练掌握多边形的内角和外角、角平分线的定义、余角的性质是解题的关键.
34.(1)
(2)见解析
【分析】(1)根据角平分线的定义分别求出和的度数,再利用三角形外角性质求出的度数;
(2)由三角形外角的性质可得,再由角平分线的定义可得,,则可求得,从而可得到的关系.
【详解】(1)解:平分,平分,
,,
,
;
(2)证明:为的外角,
,
平分,平分,
,,
是的外角,
.
【点睛】本题主要考查三角形的外角性质,角平分线的定义,解答的关键是结合图形分析清楚各角之间的关系.
35.(1)
(2)
【分析】(1)根据三角形中线性质可以求出结果;
(2)根据是的中线,与的周长差为,可得到,根据的周长为,,即可得到,进而可求出的长.
【详解】(1)解:是的中线,
,
是的中线,
;
(2)是的中线,与的周长差为,
,
的周长为,,
,
,
.
【点睛】本题考查了三角形中线的性质,根据题意找到,的关系是解答本题的关键.
36.(1)
(2)
(3)
【分析】(1)利用三角形内角和定理求得,再由,可得,即可求解;
(2)由角平分线的定义可得,再由直角三角形的性质可得,再根据三角形外角的性质可得,即可求解;
(3)根据角平分线的定义可得,再由三角形外角的性质可得,由
,,求得,再由角平分线的定义可得,最后根据三角形外角的性质即可求解.
【详解】(1)解:∵,
∴,
∵,
∴,即,
∴;
(2)解:∵平分,,
∴,
∵,
∴,
∴,
∴,
∵,
∴;
(3)解:∵平分,,
∴,
∵,,
∴,,
∵平分,
∴,
∴.
【点睛】本题考查角平分线的性质、直角三角形的性质、三角形内角和定理和三角形的性质,熟练掌握相关性质是解题的关键.
37.(1)见解析
(2)
(3)
【分析】(1)根据三角形内角和对顶角相等结合等式性质即可得出结论;
(2)连接,由(1)中得出的“字形”的性质结合三角形内角和定理即可求出结果;
(3)由角平分线性质得到,,由“字形”可知:,得出,再根据,,整理即可得到.
【详解】(1)证明:,,
又,
;
(2)如图:连接,
由(1)可知与相交,连接,,图形称为“字形”,
,
;
(3),理由如下:
如图:
平分,平分,
,,
由“字形”可知:,
即,
,,
.
.
【点睛】本题考查了三角形内角和定理,三角形外角性质,角平分线定义,对顶角相等,理解题意灵活运用题中得出的“字形”性质,是解答本题的关键.
38.(1)
(2)能,理由见解析
【分析】(1)由三角形内角和定理得度数,再根据角平分线定义得到,根据得,然后利用进行计算即可;
(2)结合,由三角形内角和定理得度数,再根据角平分线定义得到,根据得,然后利用进行计算即可.
【详解】(1)解:,,
,
平分,
,
,,
,
;
(2)能,理由如下:
,
,
平分,
,
,
,
.
【点睛】本题主要考查了三角形内角和定理,角平分线定义,熟练掌握三角形内角和定理是解答本题的关键.
39.(1)
(2)或或
(3)①见解析;②见解析
【分析】(1)根据是的“二倍角”,得出,结合,即可求出的度数;
(2)分情况讨论:当或或或时,分别计算即可;
(3)①根据角平分线的定义得出,根据平行线的性质得出,于是有,再根据邻补角互补得出,根据直角三角形两锐角互余得出,通过计算得出,问题得证;
②根据角平分线的定义结合①中的结论先求出,即,从而问题得证.
【详解】(1)解:在中,,
∴,
∵是的“二倍角”,
∴,
∴,
∴,
∴,
故答案为:;
(2)在中,,
∵有一个角是另一个角的“二倍角”,
∴或或或,
当时,;
当时,,此时∠A=45°;
当时,由(1)可知;
当时,,解得;
综上,的度数为或或;
故答案为:或或;
(3)①证明:平分,
,
,
,
,即:,
,
,
,
,
,
即:是的“二倍角”;
②证明:平分,
,
由①知,即,
,
即,
,
,
即是的“二倍角”.
【点睛】本题考查了三角形的内角和定理,平行线的性质,角平分线的定义,分类讨论思想的运用,注意不要丟解.
40.(1)①;②,理由见解析
(2)
【分析】(1)①根据三角形的内角和及平行线的性质可知,再利用角平分线的定义即可解答;②根据三角形外角的性质及平行线的性质得到,再根据三角形内角和定理及角平分线的定义即可解答;
(2)根据平行线的性质及角平分线的定义得到,再根据角平分线的定义及外角的性质即可解答.
【详解】(1)解:①,
∴在中,,
,
,
平分,
,
,
故答案为:;
②是是一个外角,
,
,
,
,
,
∵BD平分平分,
,,
,
,
,
,
;
(2)解:,
,
是的平分线,
,
,
,
平分,
,
.
【点睛】本题考查了三角形的内角和定理、平行线的性质、角平分线的定义、三角形外角的性质,熟练掌握以上知识点是解题的关键.
一、单选题
1.(2023秋·黑龙江齐齐哈尔·八年级校联考阶段练习)如图,在中,,,、的平分线相交于,过点作,交于,交于,那么下列结论正确的是( )
①;②;③;④.
A.①② B.③④ C.①③ D.①②④
2.(2023秋·安徽阜阳·八年级统考阶段练习)如图,把三角形纸片沿折叠,当点落在三角形内部时,与,之间的数量关系是( )
A. B.
C. D.
3.(2023秋·浙江绍兴·八年级校联考阶段练习)如图,在中,已知分别是边的中点,且阴影部分图形的面积为7,则的面积为( )
A.14 B.21 C.28 D.32
4.(2023秋·山东临沂·八年级临沂第九中学校考阶段练习)如图,是边的中线,点E在上,,的面积是3,则的面积是( )
A.4 B.3 C.2 D.1
5.(2023秋·浙江绍兴·八年级校联考阶段练习)已知的三个内角满足,则这个三角形是( )
A.钝角三角形 B.直角三角形 C.任意三角形 D.锐角三角形
6.(2023秋·安徽阜阳·八年级统考阶段练习)如图,在中,,,是上一点,若为直角三角形,则的度数为( )
A. B. C.或 D.或
7.(2023秋·广东东莞·八年级东莞市东华初级中学校考阶段练习)如图,中,于点D,则下列结论不一定成立的是( )
A. B. C. D.
8.(2023秋·湖北十堰·八年级校联考阶段练习)如图,点D,E分别在上,连接.若于D,,则的大小为()
A. B. C. D.
9.(2023秋·陕西延安·八年级统考阶段练习)若一个多边形从一个顶点出发可引4条对角线,则这个多边形对角线的总数为( )
A.14 B.28 C.24 D.20
10.(2023秋·山东临沂·八年级临沂第九中学校考阶段练习)如图,已知是的边上的中线,若,,的周长比的周长多2,则的长为( )
A.14 B.12 C.10 D.8
11.(2023秋·湖北武汉·八年级校考阶段练习)如图,在中,、分别是高和角平分线,点在的延长线上,交于,交于,下列结论:①;②;③;④,正确的个数是( )
A.1 B.2 C.3 D.4
12.(2023秋·广东广州·八年级校考阶段练习)如图1,线段、相交于点O,连接、,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,和的平分线和相交于点P,并且与、分别相交于M、N.其中正确的结论是( )
(1)在图1中;(2)在图2中“8 字形”的个数为 4;(3)图2中,当度,度时,度;(4)图2中和为任意角时其他条件不变.
A.(1)(2)(3) B.(1)(2)(4) C.(1)(3)(4) D.(1)(2)(3)(4)
13.(2023秋·山东日照·八年级校考阶段练习)多边形的内角和增加180°,则它的边数( )
A.增加1 B.增加2 C.增加3 D.不变
14.(2023秋·安徽淮南·八年级校联考阶段练习)以某公园西门为原点建立平面直角坐标系,东门
和景点的坐标分别是和.如图1,甲的游览路线是:,其折线段的路程总长记为.如图2,景点和分别在线段,上,乙的游览路线是:,其折线段的路程总长记为.如图3,景点和分别在线段,上,景点在线段上,丙的游览路线是:,其折线段的路程总长记为.下列的大小关系正确的是( )
A. B.且
C. D.且
15.(2023秋·广东江门·八年级校考阶段练习)如图,是的中线,是的中线.若的面积是12,则的面积是( )
A.8 B.6 C.4 D.3
16.(2023秋·湖北武汉·八年级校联考阶段练习)如图,在五边形中,,分别是的外角,则的度数为( )
A. B. C. D.
17.(2023秋·河北石家庄·八年级统考阶段练习)如图,在中,,是高,是中线,是角平分线,交于点G,交于H,下列说法正确的是( )
①;②;③;④.
A.①③ B.①②③ C.①③④ D.②③④
18.(2023秋·陕西延安·八年级校联考阶段练习)如图,,分别是的角平分线和高,若,,则的度数为( )
A. B. C. D.
19.(2023秋·天津静海·八年级校考阶段练习)如图,在中,,和的平分线相交于点G,则的度数为( )
A. B. C. D.
20.(2023秋·黑龙江齐齐哈尔·八年级统考阶段练习)如图,在中,,,、的平分线相交于,过点作,交于,交于,那么下列结论正确的是( )
①;②;③;④.
A.①② B.③④ C.①③ D.①②③
二、填空题
21.(2023秋·湖北武汉·八年级校联考阶段练习)如图,点G为的三条中线的交点,,若
,则面积的最大值是 .
22.(2023秋·陕西延安·八年级统考阶段练习)如图,处在处的南偏西方向,处在处的南偏东方向,处在处的北偏东方向,则的度数为 .
23.(2023秋·湖北随州·八年级校考阶段练习)如图,,分别是,的中点,若,则 .
24.(2023秋·山东临沂·八年级临沂第九中学校考阶段练习)如图,在中,,点D、E分别是,上一点,将沿折叠,使点A落在点F处,已知,的度数 .
25.(2023秋·安徽阜阳·八年级统考阶段练习)如图,和是的两个外角,若,则的度数为 .
26.(2023秋·陕西延安·八年级统考阶段练习)如图,正六边形和正五边形的边
重合,的延长线与交于点,则的度数是 .
27.(2023秋·广东东莞·八年级东莞市东华初级中学校考阶段练习)在中,若,则 .
28.(2023秋·湖北黄冈·八年级校联考阶段练习)如图,是的角平分线,,垂足为,连接.若,,则的度数为 .
29.(2023秋·全国·八年级专题练习)如图,在中,,和的平分线交于点,得;和的平分线交于点,得;…;和的平分线交于点,则 °.
30.(2023秋·内蒙古呼和浩特·八年级校考阶段练习)如图,是的角平分线,D是边上一点,交于点F,若,,则的度数为 .
三、解答题
31.(2023秋·陕西商洛·八年级校考阶段练习)如图,是的角平分线,过点作交的延长线于点,点在边上,连接交于点.
若,求证:;(2)若,求的度数.
32.(2023秋·辽宁大连·八年级统考阶段练习)(1)如图,的外角和的平分线交于点F.用等式表示与的数量关系;
(2)如图,的平分线和的外角的平分线交于点H.用等式表示与的数量关系,并证明.
33.(2023秋·辽宁大连·八年级校联考阶段练习)如图,在四边形中,,平分,平分.求证.
34.(2023秋·安徽阜阳·八年级统考阶段练习)如图,在中,与外角的角平分线相交于点.
(1)当,时,求的度数;(2)求证:.
35.(2023秋·安徽阜阳·八年级统考阶段练习)如图,在中,是的中线,是的中线.
(1)若,求的长;(2)若的周长为,,且与的周长差为,求的长.
36.(2023秋·广东东莞·八年级东莞市东华初级中学校考阶段练习)在中,平分交于点D,
(1)求的度数;
(2)如图①,若于点F,交于点E.求的度数.
(3)如图②,若平分交于点E,交于点F,求的度数.
37.(2023秋·安徽阜阳·八年级统考阶段练习)如图1,线段,相交于点,连接,,我们把形如图的图形称为“字形”.
(1)求证:;
(2)如图2,求的度数;
(3)如图3,平分,平分的邻补角,试猜想,与之间的数量关系,并说明理由.
38.(2023秋·安徽阜阳·八年级统考阶段练习)如图,与分别是的角平分线和高.
(1)已知,,求度数;
(2)探究:小明认为如果只知道,也能得出的度数,你认为可能吗?若能,请你写出求解过程;若不能,请说明理由.
39.(2023秋·河北沧州·八年级校考阶段练习)如果一个角是另一个角的2倍,那么称是的“二倍角”.例如:,,则是的“二倍角”.已知在中,.
(1)若是的“二倍角”,则______;
(2)若的三个内角中,有一个角是另一个角的“二倍角”,则______;
(3)如图1,作的外角平分线,过点作的平行线.
①求证:是的“二倍角”;
②如图2,再作的角平分线,求证:是的“二倍角”.
40.(2023秋·全国·八年级专题练习)在中,BD平分交于点,点是线段上的动点(不与点重合),过点作交射线于点,的平分线所在直线与射线交于点.
(1)如图,点在线段上运动.
①若,则的度数是 ;的度数是 ,
②探究与之间的数量关系,并说明理由;
(2)若点在线段上运动时,请直接写出与之间的数量关系.
参考答案:
1.C
【分析】根据三角形内角和定理对进行判断;根据角平分线的定义和三角形内角和定理可得到,则可对进行判断;根据平行线的性质对进行判断;先根据角平分线的性质得到,然后根据平行线的性质对进行判断.
【详解】解:,,
∴,所以正确;
、的平分线相交于,
∴,,
∴,所以错误;
∵,
∴,所以正确;
平分,
∴,
∵,
∴,所以错误;
综上分析可知,①③正确.
故选:C.
【点睛】本题考查了平行线的性质,三角形的内角和定理的应用,角平分线的定义,掌握以上基础知识是解本题的关键.
2.A
【分析】首先根据折叠性质可得,,利用邻补角可得,,在中,根据三角形内角和定理可得,整理即可得出结果.
【详解】解:如图
三角形纸片沿折叠,当点落在三角形内部,
,,
,,
,,
在中,,
,
整理得:,
故选:.
【点睛】本题考查了三角形内角和定理,折叠性质,邻补角定义,熟练掌握三角形内角和定理是解答本题的关键.
3.C
【分析】由是的中点可得,由是的中点可得,,从而得到,再由即可得到答案.
【详解】解:是的中点,
,
是的中点,
,,
,
,
,
故选:C.
【点睛】本题考查了与中线有关的三角形面积的计算,利用题中所给的条件,将面积进行转化是解此题的关键.
4.D
【分析】利用三角形面积公式,等高的三角形的面积比等于底边的比,由此利用已知条件可以分别求出.
【详解】解:∵是边的中线,的面积是3,
∴,
∵,
∴,
故选:D.
【点睛】本题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半;三角形的中线将三角形分成面积相等的两部分.
5.B
【分析】设,,,根据三角形内角和定理可得,求出的值即可得到答案.
【详解】解:的三个内角满足,
设,,,
,
,
解得:,
,
这个三角形是直角三角形,
故选:B.
【点睛】本题考查了三角形内角和定理,熟练掌握三角形内角和为是解题的关键.
6.C
【分析】利用三角形内角和先求出的度数,再根据点的位置不同分情况利用求出的度数,进而求出的度数.
【详解】解:在中,,,
,
如图,当时,
,
,
,
当时,
.
故选:.
【点睛】本题考查了三角形内角和定理,熟练掌握三角形内角和定理是解答本题的关键.
7.B
【分析】根据直角三角形的性质可得,再由,可得,再根据等角的余角相等可得,,即可求解.
【详解】解:∵,
∴,故A选项不符合题意;
∵,
∴,
∴,故选项C不符合题意;
又∵,
∴,
∴不一定成立,故B选项符合题意;
∵,,
∴,故D选项不符合题意;
故选:B.
【点睛】本题考查直角三角形的性质、余角的性质,利用直角三角形的性质和等角的余角相等得出,,是解题的关键.
8.D
【分析】由三角形的内角和定理和平角定义,可得由此解答即可.
【详解】解:∵
,,
,
,
,
,
故选:D.
【点睛】本题考查了三角形内角和定理和三角形外角性质,掌握这些知识点是解题的关键.
9.A
【分析】根据一个边形从一个顶点出发有条对角线,即可求出该多边形的边数.再根据边形对角线的总数为,即可求解.
【详解】解:根据题意,一个多边形从一个顶点出发可引4条对角线,
可知该多边形的边数为,
∴这个多边形对角线的总数为.
故选:A.
【点睛】本题主要考查了多边形的对角线的条数问题,熟练掌握边形的相关公式是解题关键.
10.C
【分析】依据 是 的边 上的中线,可得 ,再根据 的周长比 的周长多 2 , 即可得到 的长;
【详解】解:∵ 是 的边 上的中线,
又 ∵ 的周长比 的周长多2 ,
即 ,
故选 :C.
【点睛】本题考查了三角形的中线, 求出两个三角形的周长的差等于两边的差是解题的关键.
11.C
【分析】①根据,,以及即可推出;②根据角平分线的定义和三角形外角的性质证明即可;③证明,由①知:即可证明
;④由同角的余角相等证明,再根据三角形外角的性质及角平分线的性质即可推出,即可判断.
【详解】解:∵,
∴.
∵,
∴.
∵,
∴.
故①正确;
∵平分,
∴.
∵,
∴.
∵,
∴.
故②正确;
∵平分,
∴.
∵,
∴.
∴.
由①知:,
∴.
故③正确;
∵,
∴.
∴.
∵平分,
∴,
∴.
∴
故④错误;
综上可知,正确的有①②③,共3个,
故选C.
【点睛】本题主要考查了三角形的内角和定理,三角形外角的性质,同角的余角相等等知识,正确运用三角形的高、角平分线的概念以及三角形的内角和定理是解题的关键.
12.C
【分析】根据对顶角相等可得,再根据三角形的内角和定理即可判断(1)正确;根据“8字形”的定义即可判断(2)错误;如图(见解析),根据角平分线的定义可得,再根据结论(1)可得,,两式相加即可判断(4)正确;将度,度代入结论(4)计算即可判断(3)正确.
【详解】解:,,
,则结论(1)正确;
在图2中,线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
线段、相交于点,连接、,形成“8字形”,
在图2中“8 字形”共有6个,则结论(2)错误;
如图,和的平分线和相交于点,
,
同结论(1)可知,,,
两式相加得:,
,则结论(4)正确;
则当度,度时,,
解得度,则结论(3)正确;
综上,正确的结论是(1)(3)(4),
故选:C.
【点睛】本题考查了三角形的内角和定理、角平分线的定义等知识点,掌握理解“8 字形”的定义是解题关键.
13.A
【分析】根据多边形的内角和公式,可知多边形的内角和是的整数倍,可得多边形的内角和增加180°,它就增加1条边.
【详解】∵多边形的内角和是,
∴多边形的内角和增加180°,它的边数就增加1.
故选:A.
【点睛】本题主要考查了多边形内角和与边数的关系,解决问题的关键是熟练掌握多边形的内角和公式.
14.D
【分析】根据三角形三边的关系即可证明,根据平移的性质可证明.
【详解】解:根据题意可得,,
∴;
将线段平移,可得到线段,线段移可得到线段,
∴,,
,
∴,
故选:D.
【点睛】本题考查了三角形三边关系,平移的性质,题目新颖,灵活运用所学知识是解题的关键.
15.D
【分析】根据的面积是12,三角形中线将三角形面积两等分,即可求解.
【详解】解:∵是的中线,
∴,
∵是的中线,
∴,
故选:D.
【点睛】本题考查三角形的中线及三角形面积公式,掌握三角形的中线将三角形面积两等分是解题的关键.
16.A
【分析】如图,反向延长,根据平行线的性质可得,再结合多边形外角和定理即可求解.
【详解】解:反向延长,
∵,
∴,
根据多边形的外角和定理可得,
∴.
故选A.
【点睛】本题考查多边形外角和问题,平行线的性质,解题的关键是掌握多边形外角和为360度.
17.C
【分析】根据三角形内角和定理求出,根据三角形的外角性质即可推出①;根据等腰三角形的判定判断②即可;根据三角形内角和定理求出,根据角平分线定义即可判断③;根据等底等高的三角形的面积相等即可判断④.
【详解】解:∵是角平分线,
∴,
∵为高,
∴,
∵,
∴,
∴,
故①正确;
根据已知条件不能推出,即不能推出,
故②错误;
∵为高,
∴,
∵,
∴,
∴,
∵是角平分线,
∴,
∴,
即,
故③正确;
∵是中线,
∴,
∴(等底等高的三角形的面积相等),
故④正确.
故选:C.
【点睛】本题考查了三角形内角和定理,三角形的外角性质,三角形的角平分线、中线、高,等腰三角形的判定等知识点,能综合运用定理进行推理是解此题的关键.
18.B
【分析】利用三角形内角和定理求出,再根据角平分线和高线,可求出和,进而可求出的度数.
【详解】解:,,
,
是的角平分线,
,
又是的高,
,
,
.
故选:B.
【点睛】本题考查了三角形的内角和定理、角平分线的性质等知识点,解题的关键是掌握三角形的内角和定理.
19.D
【分析】先利用角平分线的性质和三角形的内角和定理求出与和的度数,再利用三角形的外角和内角的关系得结论.
【详解】解:、分别是和的平分线,
,.
,,
.
,
,
.
故选:D.
【点睛】本题主要考查了三角形的内角和定理及推论,掌握“三角形的内角和是”、“三角形的外角等于与它不相邻的两个内角的和”及角平分线的定义是解决本题的关键.
20.C
【分析】根据三角形内角和定理对进行判断;根据角平分线的定义和三角形内角和定理可得到,则可对进行判断;根据平行线的性质对进行判断;先根据角平分线的性质得到,然后根据平行线的性质对进行判断.
【详解】解:,,
∴,所以正确;
、的平分线相交于,
∴,所以错误;
∵,
∴,所以正确;
平分,
∴,
∵,
∴,所以错误;
综上分析可知,①②③正确.
故选:C.
【点睛】本题考查了等腰三角形的判定与性质:平行线的性质,等腰三角形提供了好多相等的线段和相等的角,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.
21.4
【分析】由三角形的面积关系可证,即可求解.
【详解】解:点为的三条中线的交点,
,是的中线,
,,,即,
,
,
,
,
,
当时,面积有最大值,
∵,
面积的最大值,
故答案为4
【点睛】本题考查了三角形的中线与面积的关系,理解题意是解题的关键.
22./度
【分析】根据平行线的性质,可得内错角相等,根据角的和差,可得、,根据三角形的内角和公式,可得答案.
【详解】解:如图,
根据方向角的定义,可得.
∵,
∴.
∵是正南正北方向,
∴,
又∵,
∴,
.
故答案为:
【点睛】本题主要考查了方向角的定义,平行线的性质以及三角形的内角和定理,正确理解定义是解题的关键.
23.4
【分析】三角形的中线将三角形分成面积相等的两部分,据此可得,.
【详解】解:∵点是的中点,
∴,
∵点是的中点,
∴.
故答案为:4.
【点睛】本题主要考查了三角形中线有关的面积计算,解题关键是理解并掌握三角形中线的定义和性质.
24.
【分析】由折叠可知:,由三角形的内角和定理可求,即可求得,再利用三角形的内角和定理可求,进而可求解.
【详解】解:由折叠可知:,
∵,
∴,
∴,
∵,
∴,
∴.
故答案为:
【点睛】本题主要考查三角形的内角和定理,翻折问题,掌握三角形的内角和定理是解题的关键.
25./234度
【分析】根据三角形的外角的性质和三角形的内角和定理即可得到结论.
【详解】解:和是的两个外角,
,
,
.
故答案为:.
【点睛】本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形外角的性质是解答此题的关键.
26./84度
【分析】利用多边形的内角和与正多边形的性质分别求得的度数,然后利用等边对等角及三角形内角和定理求得的度数,再结合四边形的内角和为进行计算即可.
【详解】解:∵六边形为正六边形,
∴,
∵五边形为正五边形,
∴,
∴,
∵四边形的内角和为,
∴,
故答案为:.
【点睛】本题主要考查多边形的内角和及正多边形的性质,结合已知条件求得的度数是解题的关键.
27./75度
【分析】由:,,,可得出,求得,最后求得.
【详解】解:,,
又,
,
,
.
故答案为:.
【点睛】本题考查了三角形内角和定理,牢记“三角形内角和是”是解题的关键.
28./28度
【分析】在中,利用三角形内角和定理,可求出的度数,由平分,利用角平分线的定义,可求出的度数,在中,利用三角形内角和定理,可求出的度数,再结合,即可求出的度数.
【详解】解:在中,,,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴.
故答案为:.
【点睛】本题主要考查了三角形内角和定理以及角平分线的定义,牢记“三角形内角和是
”是解题的关键.
29./
【分析】根据角平分线的性质和三角形外角性质得出和的关系,进而求出与的关系,找出规律,得到与的关系即可求解.
【详解】解:和的平分线交于点,
,
,
同理,,
,
,
当时,,
(度)
故答案为:.
【点睛】本题考查了三角形外角性质与角平分线的定义,找出规律是解题的关键.
30./79度
【分析】角平分线得到,根据已知条件得到,得到,根据三角形的内角和定理,得到,求出的度数,再根据三角形的内角和定理以及对顶角相等,即可得出结果.
【详解】解:如图,
∵是的角平分线,
∴,
∵,,
∴,
∴,
∵,
∴,
∴;
故答案为:.
【点睛】本题考查与角平分线有关的三角形的内角和问题.熟练掌握角平分线平分角,以及三角形的内角和为,是解题的关键.
31.(1)见解析
(2)
【分析】(1)先根据垂直等于得到,则,再证明,加上,则,然后根据平行线的判定方法得到结论;
(2)先根据三角形内角和定理可计算出,则,根据三角形内角和定理得到,即,从而可求出的度数.
【详解】(1)证明:,
,
,
是的角平分线,
,
,
即,
,
,
;
(2)解:,,
,
,
,
,
即,
.
【点睛】本题考查了三角形内角和定理、平行线额判定,解题的关键是运用三角形内角和定理可根据两已知角求第三个角.
32.(1);(2).见解析
【分析】(1)利用角平分线的性质和三角形的外角性质可求出,再利用三角形内角和定理即可求出的度数.
(2)先根据三角形的外角性质得到,再根据角平分线的定义解答即可.
【详解】解:(1)∵为两外角的平分线,
∴;
由三角形内角和定理得:
(2)
证明:∵的外角的平分线和的平分线交于点H,
∴.
∵,
∴.
∴
∴.
【点睛】本题考查三角形的内角和定理,三角形外角的性质,角平分线的定义,熟练掌握三角形的内角和定理以及三角形外角的性质是解题的关键.
33.见解析
【分析】根据四边形的内角和得到,根据角平分线的定义得到,则,再因为在中,,根据余角的性质即可得出结论.
【详解】证明:∵在四边形中,,,
∴.
∵平分,平分,
∴,
∴
∵在中,,
∴.
【点睛】本题主要考查多边形的内角和外角,角平分线的定义,余角的性质,熟练掌握多边形的内角和外角、角平分线的定义、余角的性质是解题的关键.
34.(1)
(2)见解析
【分析】(1)根据角平分线的定义分别求出和的度数,再利用三角形外角性质求出的度数;
(2)由三角形外角的性质可得,再由角平分线的定义可得,,则可求得,从而可得到的关系.
【详解】(1)解:平分,平分,
,,
,
;
(2)证明:为的外角,
,
平分,平分,
,,
是的外角,
.
【点睛】本题主要考查三角形的外角性质,角平分线的定义,解答的关键是结合图形分析清楚各角之间的关系.
35.(1)
(2)
【分析】(1)根据三角形中线性质可以求出结果;
(2)根据是的中线,与的周长差为,可得到,根据的周长为,,即可得到,进而可求出的长.
【详解】(1)解:是的中线,
,
是的中线,
;
(2)是的中线,与的周长差为,
,
的周长为,,
,
,
.
【点睛】本题考查了三角形中线的性质,根据题意找到,的关系是解答本题的关键.
36.(1)
(2)
(3)
【分析】(1)利用三角形内角和定理求得,再由,可得,即可求解;
(2)由角平分线的定义可得,再由直角三角形的性质可得,再根据三角形外角的性质可得,即可求解;
(3)根据角平分线的定义可得,再由三角形外角的性质可得,由
,,求得,再由角平分线的定义可得,最后根据三角形外角的性质即可求解.
【详解】(1)解:∵,
∴,
∵,
∴,即,
∴;
(2)解:∵平分,,
∴,
∵,
∴,
∴,
∴,
∵,
∴;
(3)解:∵平分,,
∴,
∵,,
∴,,
∵平分,
∴,
∴.
【点睛】本题考查角平分线的性质、直角三角形的性质、三角形内角和定理和三角形的性质,熟练掌握相关性质是解题的关键.
37.(1)见解析
(2)
(3)
【分析】(1)根据三角形内角和对顶角相等结合等式性质即可得出结论;
(2)连接,由(1)中得出的“字形”的性质结合三角形内角和定理即可求出结果;
(3)由角平分线性质得到,,由“字形”可知:,得出,再根据,,整理即可得到.
【详解】(1)证明:,,
又,
;
(2)如图:连接,
由(1)可知与相交,连接,,图形称为“字形”,
,
;
(3),理由如下:
如图:
平分,平分,
,,
由“字形”可知:,
即,
,,
.
.
【点睛】本题考查了三角形内角和定理,三角形外角性质,角平分线定义,对顶角相等,理解题意灵活运用题中得出的“字形”性质,是解答本题的关键.
38.(1)
(2)能,理由见解析
【分析】(1)由三角形内角和定理得度数,再根据角平分线定义得到,根据得,然后利用进行计算即可;
(2)结合,由三角形内角和定理得度数,再根据角平分线定义得到,根据得,然后利用进行计算即可.
【详解】(1)解:,,
,
平分,
,
,,
,
;
(2)能,理由如下:
,
,
平分,
,
,
,
.
【点睛】本题主要考查了三角形内角和定理,角平分线定义,熟练掌握三角形内角和定理是解答本题的关键.
39.(1)
(2)或或
(3)①见解析;②见解析
【分析】(1)根据是的“二倍角”,得出,结合,即可求出的度数;
(2)分情况讨论:当或或或时,分别计算即可;
(3)①根据角平分线的定义得出,根据平行线的性质得出,于是有,再根据邻补角互补得出,根据直角三角形两锐角互余得出,通过计算得出,问题得证;
②根据角平分线的定义结合①中的结论先求出,即,从而问题得证.
【详解】(1)解:在中,,
∴,
∵是的“二倍角”,
∴,
∴,
∴,
∴,
故答案为:;
(2)在中,,
∵有一个角是另一个角的“二倍角”,
∴或或或,
当时,;
当时,,此时∠A=45°;
当时,由(1)可知;
当时,,解得;
综上,的度数为或或;
故答案为:或或;
(3)①证明:平分,
,
,
,
,即:,
,
,
,
,
,
即:是的“二倍角”;
②证明:平分,
,
由①知,即,
,
即,
,
,
即是的“二倍角”.
【点睛】本题考查了三角形的内角和定理,平行线的性质,角平分线的定义,分类讨论思想的运用,注意不要丟解.
40.(1)①;②,理由见解析
(2)
【分析】(1)①根据三角形的内角和及平行线的性质可知,再利用角平分线的定义即可解答;②根据三角形外角的性质及平行线的性质得到,再根据三角形内角和定理及角平分线的定义即可解答;
(2)根据平行线的性质及角平分线的定义得到,再根据角平分线的定义及外角的性质即可解答.
【详解】(1)解:①,
∴在中,,
,
,
平分,
,
,
故答案为:;
②是是一个外角,
,
,
,
,
,
∵BD平分平分,
,,
,
,
,
,
;
(2)解:,
,
是的平分线,
,
,
,
平分,
,
.
【点睛】本题考查了三角形的内角和定理、平行线的性质、角平分线的定义、三角形外角的性质,熟练掌握以上知识点是解题的关键.
