21.1一元二次方程 教案(表格式)初中数学人教版九年级上册
文档属性
| 名称 | 21.1一元二次方程 教案(表格式)初中数学人教版九年级上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 407.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 17:37:29 | ||
图片预览


文档简介
《一元二次方程》教学设计
姓名 / 学号 /
教材分析 一元二次方程(第1课时)是人教版《义务教育教科书·数学》九年级上册第二十一章第1节的内容。本节内容的教学分为1个课时。这一课时是在学生已经掌握一元一次方程和二元一次方程组的概念的基础上,通过探究实际问题从而引出一元二次方程的概念,进而掌握一元二次方程的一般形式。一元二次方程是初中重要的教学内容,本节课的内容是后续学习解一元二次方程做好铺垫,也为将来学习二次函数,二次不等式、高次方程打下基础。
学情分析 九年级的学生有了一定的类比推理能力和合作探究能力。在此基础上本节课学习,降低了本节课授课难度,学生渴望在数学探究中享受成功的喜悦,让他们在探究一元二次方程概念中发表他们的观点,激发他们学习数学的兴趣。学生具有数据分析的能力,在学习一元二次方程的过程中可以大胆猜想结论,但是学生运用综合知识的能力不强,难于用一元二次方程解决实际问题,所以还需要对学生的综合能力进行提高。
教学目标 知识与技能 理解一元二次方程和根的概念,掌握一元二次方程的一般形式,会判断各项系数。
过程与方法 经过对实际问题的探究过程中得出一元二次方程的概念,从而培养数据分析和分析问题以及解决问题和提炼模型的能力。
情感态度价值观 通过在实际问题学习数学,使学生认识到数学与实际生活密切联系,从而激发学生学习数学的兴趣。
教学重点 一元二次方程的概念以及根据一元二次方程的一般形式,确定各项系数
教学难点 理解一元二次方程的概念,在实际问题中列出方程
教法学法 启发引导法、直观演示法、练习法
教学程序
教学环节 教学内容 师生互动 设计意图
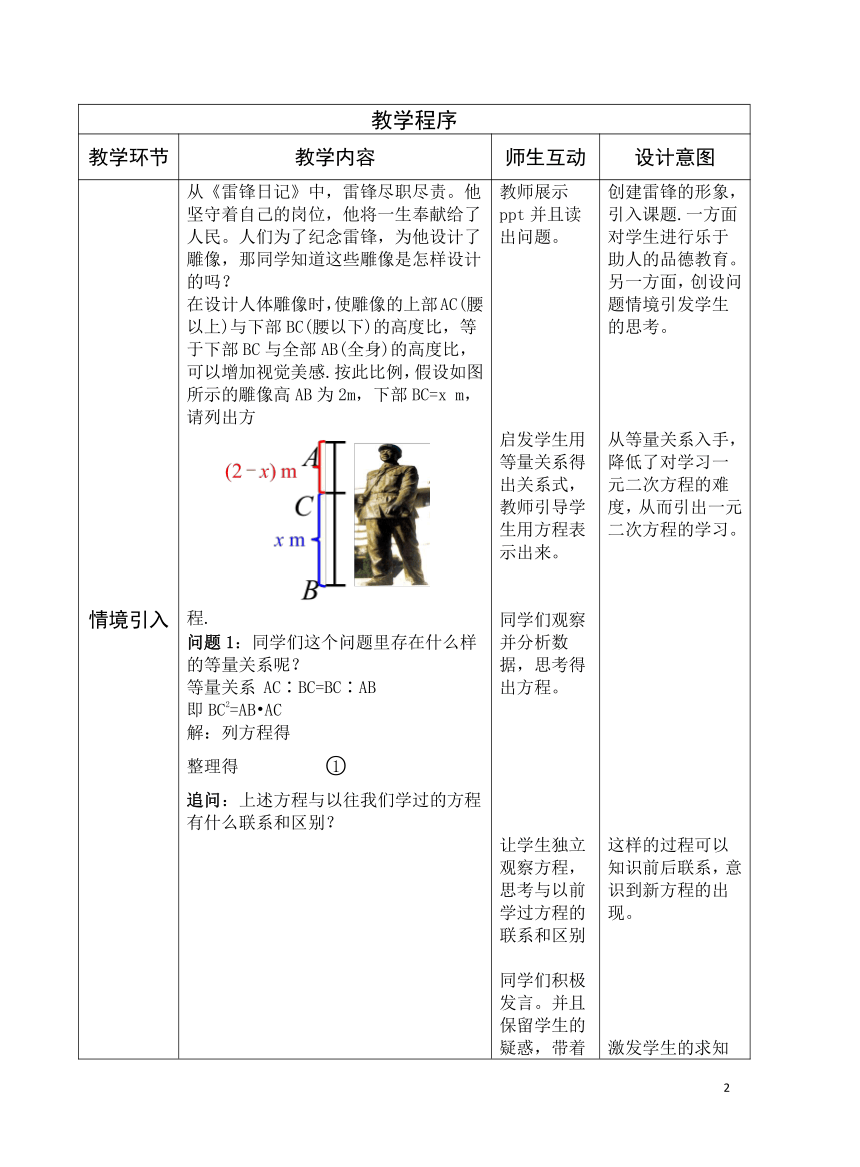
情境引入 从《雷锋日记》中,雷锋尽职尽责。他坚守着自己的岗位,他将一生奉献给了人民。人们为了纪念雷锋,为他设计了雕像,那同学知道这些雕像是怎样设计的吗?在设计人体雕像时,使雕像的上部AC(腰以上)与下部BC(腰以下)的高度比,等于下部BC与全部AB(全身)的高度比,可以增加视觉美感.按此比例,假设如图所示的雕像高AB为2m,下部BC=x m,请列出方程.问题1:同学们这个问题里存在什么样的等量关系呢?等量关系 AC∶BC=BC∶AB即BC2=AB AC解:列方程得整理得追问:上述方程与以往我们学过的方程有什么联系和区别? 教师展示ppt并且读出问题。启发学生用等量关系得出关系式,教师引导学生用方程表示出来。同学们观察并分析数据,思考得出方程。让学生独立观察方程,思考与以前学过方程的联系和区别同学们积极发言。并且保留学生的疑惑,带着疑问去寻找答案 创建雷锋的形象,引入课题.一方面对学生进行乐于助人的品德教育。另一方面,创设问题情境引发学生的思考。从等量关系入手,降低了对学习一元二次方程的难度,从而引出一元二次方程的学习。这样的过程可以知识前后联系,意识到新方程的出现。激发学生的求知欲
讲授新课 问题2:有一块矩形铁皮,长100cm,宽50cm,在它的四角各切去一个正方形,然后将四周凸出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600cm2,那么铁皮各角应切去多大的正方形?请根据题意列出方程解:设切去的正方形的边长为xcm,则盒底的长为(100-2x)cm,宽为(50-2x)cm,根据方盒的底面积为3600cm2,得整理,得化简得问:该方程中未知数的个数和最高次数各是多少?问题3:要组织要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛 解析:设应邀请x个队参赛,每个队都要与其他(x-1)个队各赛一场,因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共场.解:根据题意,列方程:整理,得化简得探究1:方程①②③是不是一元一次方程?那么这三个方程与一元一次方程的区别在哪里?方程①②③有什么共同点?方程两边都是等式吗?概念归纳一元二次方程的概念像这样的等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程叫做一元二次方程。都只有一个未知数它们的最高次数都是2方程两边都是整式一元二次方程的一般形式是ax2+bx+c=0(a≠0)ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.探究2:想一想:为什么一元二次方程的一般形式ax2+bx+c=0中要限制a≠0?b,c可以为0吗?当a=0时,bx+c=0,不符合定义当a≠0,b=0时,ax2+c=0,符合定义当a≠0,c=0时,ax2+bx=0,符合定义当a≠0,b=c=0时ax2=0,符合定义一元二次方程的根的定义使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根下面哪些数是方程x2–x–6=0的解 -4,-3,-2,-1,0,1,2,3,43、-2你注意到了吗?一元二次方程可能不止一个根排球赛问题中的根8和-7追问:在实际问题中根能不能为负数归纳:1、一元二次方程根的情况2、根是不是满足实际情况 学生看PPT思考问题学生和教师设未知数,找出等量关系列出方程。找学生回答问题。小组合作讨论所得的三个方程整理后的特点,找出与一元一次方程的区别和联系。教师引导学生初步得出一元二次方程的概念解决问题1中的疑惑师生一起分析一元二次方程的一般形式教师启发学生用一元二次方程的概念来进行思考学生思考回答教师给出根的概念给出例题让学生讨论一元二次方程和一元一次方程根的区别,和在一些实际问题中根能不能为负数?停止讨论,让同学积极举手回答 数学问题与生活实际相联系,让同学知道数学的重要性,激发求知欲从实际问题中找出等量关系,从而列出方程,可提高学生利用方程思想解决问题的能力。在探究三个例题中得出的三个一元二次方程进行特点的归纳,提高学生归纳能力和建立数学模型的能力、合作探究能力。通过与以前知识的比较,一是对以前知识的巩固,二是对一元二次方程的认识更加清晰,加以区别,强调一元二次方程的特点。使学生更加全面理解一元二次方程的概念。强调易错点a0联系上生活实际,进一步理解根的含义
典例精析 例1下列选项中,关于x的一元二次方程的是(C)例2:将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数.去括号,得3x2-3x=5x+10.移项、合并同类项,得一元二次方程的一般形式3x2-8x-10=0其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.注:系数和项均包含前面的符号 教师分析,学生解题教师带着学生解题。A不是整式方程B含两个未知数C化简为x2-3x+2=0D化简为4x2-1=4x2+12x+9让学生上台解题教师进行点评讲解教师强调要找到个项系数要化成一般形式,系数和项均包含前面的符号 加深对概念的理解。以学生为主体是教学的基本出发点是新课改的素质教育,发挥学生主体作用。让部分学生上台写答案,师生再进行评价,教师可以及时发现问题,并且告诉学生二次项系数为正的更好。
巩固练习 例1.下列哪些是一元二次方程3x+2=5x-2 错x2=0对(x+3)(2x-4)=x2对x2=x3+x2-1错例2.填表例3.若x=3是方程x2+kx=0的一个根,试求常数k的值?x +kx=03 +3k=03k=-9k=-3 学生独立完成,老师巡视指导,出现问题是及时更正 在课堂上回顾知识,有不懂的问题可以及时询问老师,加强知识的巩固,并且了解学生的学习情况。
课堂小结 让学生总结本节课学了哪些知识,应该注意什么? 让学生对本节课的知识有一个结构的梳理,清晰知识的结构,有助于学知识的记忆。培养学生归纳概括的能力。
课后作业 必做:易:课本P4第1题1、2、4、6中:课本P4第5、6题难:课本P4第7题选做:请同学们了解一元二次方程的由来,并写出自己在这节课的收获感想。 老师布置学生按规定时间完成 课后作业对本节知识进行巩固和提高。布置分层作业尊重学生的个体差异,可以使同学们在原有的基础上提高,激发学生学习的积极性。对于难度较大的作业可以提高学生的能力。
板书设计
1
姓名 / 学号 /
教材分析 一元二次方程(第1课时)是人教版《义务教育教科书·数学》九年级上册第二十一章第1节的内容。本节内容的教学分为1个课时。这一课时是在学生已经掌握一元一次方程和二元一次方程组的概念的基础上,通过探究实际问题从而引出一元二次方程的概念,进而掌握一元二次方程的一般形式。一元二次方程是初中重要的教学内容,本节课的内容是后续学习解一元二次方程做好铺垫,也为将来学习二次函数,二次不等式、高次方程打下基础。
学情分析 九年级的学生有了一定的类比推理能力和合作探究能力。在此基础上本节课学习,降低了本节课授课难度,学生渴望在数学探究中享受成功的喜悦,让他们在探究一元二次方程概念中发表他们的观点,激发他们学习数学的兴趣。学生具有数据分析的能力,在学习一元二次方程的过程中可以大胆猜想结论,但是学生运用综合知识的能力不强,难于用一元二次方程解决实际问题,所以还需要对学生的综合能力进行提高。
教学目标 知识与技能 理解一元二次方程和根的概念,掌握一元二次方程的一般形式,会判断各项系数。
过程与方法 经过对实际问题的探究过程中得出一元二次方程的概念,从而培养数据分析和分析问题以及解决问题和提炼模型的能力。
情感态度价值观 通过在实际问题学习数学,使学生认识到数学与实际生活密切联系,从而激发学生学习数学的兴趣。
教学重点 一元二次方程的概念以及根据一元二次方程的一般形式,确定各项系数
教学难点 理解一元二次方程的概念,在实际问题中列出方程
教法学法 启发引导法、直观演示法、练习法
教学程序
教学环节 教学内容 师生互动 设计意图
情境引入 从《雷锋日记》中,雷锋尽职尽责。他坚守着自己的岗位,他将一生奉献给了人民。人们为了纪念雷锋,为他设计了雕像,那同学知道这些雕像是怎样设计的吗?在设计人体雕像时,使雕像的上部AC(腰以上)与下部BC(腰以下)的高度比,等于下部BC与全部AB(全身)的高度比,可以增加视觉美感.按此比例,假设如图所示的雕像高AB为2m,下部BC=x m,请列出方程.问题1:同学们这个问题里存在什么样的等量关系呢?等量关系 AC∶BC=BC∶AB即BC2=AB AC解:列方程得整理得追问:上述方程与以往我们学过的方程有什么联系和区别? 教师展示ppt并且读出问题。启发学生用等量关系得出关系式,教师引导学生用方程表示出来。同学们观察并分析数据,思考得出方程。让学生独立观察方程,思考与以前学过方程的联系和区别同学们积极发言。并且保留学生的疑惑,带着疑问去寻找答案 创建雷锋的形象,引入课题.一方面对学生进行乐于助人的品德教育。另一方面,创设问题情境引发学生的思考。从等量关系入手,降低了对学习一元二次方程的难度,从而引出一元二次方程的学习。这样的过程可以知识前后联系,意识到新方程的出现。激发学生的求知欲
讲授新课 问题2:有一块矩形铁皮,长100cm,宽50cm,在它的四角各切去一个正方形,然后将四周凸出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600cm2,那么铁皮各角应切去多大的正方形?请根据题意列出方程解:设切去的正方形的边长为xcm,则盒底的长为(100-2x)cm,宽为(50-2x)cm,根据方盒的底面积为3600cm2,得整理,得化简得问:该方程中未知数的个数和最高次数各是多少?问题3:要组织要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛 解析:设应邀请x个队参赛,每个队都要与其他(x-1)个队各赛一场,因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共场.解:根据题意,列方程:整理,得化简得探究1:方程①②③是不是一元一次方程?那么这三个方程与一元一次方程的区别在哪里?方程①②③有什么共同点?方程两边都是等式吗?概念归纳一元二次方程的概念像这样的等号两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程叫做一元二次方程。都只有一个未知数它们的最高次数都是2方程两边都是整式一元二次方程的一般形式是ax2+bx+c=0(a≠0)ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.探究2:想一想:为什么一元二次方程的一般形式ax2+bx+c=0中要限制a≠0?b,c可以为0吗?当a=0时,bx+c=0,不符合定义当a≠0,b=0时,ax2+c=0,符合定义当a≠0,c=0时,ax2+bx=0,符合定义当a≠0,b=c=0时ax2=0,符合定义一元二次方程的根的定义使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根下面哪些数是方程x2–x–6=0的解 -4,-3,-2,-1,0,1,2,3,43、-2你注意到了吗?一元二次方程可能不止一个根排球赛问题中的根8和-7追问:在实际问题中根能不能为负数归纳:1、一元二次方程根的情况2、根是不是满足实际情况 学生看PPT思考问题学生和教师设未知数,找出等量关系列出方程。找学生回答问题。小组合作讨论所得的三个方程整理后的特点,找出与一元一次方程的区别和联系。教师引导学生初步得出一元二次方程的概念解决问题1中的疑惑师生一起分析一元二次方程的一般形式教师启发学生用一元二次方程的概念来进行思考学生思考回答教师给出根的概念给出例题让学生讨论一元二次方程和一元一次方程根的区别,和在一些实际问题中根能不能为负数?停止讨论,让同学积极举手回答 数学问题与生活实际相联系,让同学知道数学的重要性,激发求知欲从实际问题中找出等量关系,从而列出方程,可提高学生利用方程思想解决问题的能力。在探究三个例题中得出的三个一元二次方程进行特点的归纳,提高学生归纳能力和建立数学模型的能力、合作探究能力。通过与以前知识的比较,一是对以前知识的巩固,二是对一元二次方程的认识更加清晰,加以区别,强调一元二次方程的特点。使学生更加全面理解一元二次方程的概念。强调易错点a0联系上生活实际,进一步理解根的含义
典例精析 例1下列选项中,关于x的一元二次方程的是(C)例2:将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数.去括号,得3x2-3x=5x+10.移项、合并同类项,得一元二次方程的一般形式3x2-8x-10=0其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.注:系数和项均包含前面的符号 教师分析,学生解题教师带着学生解题。A不是整式方程B含两个未知数C化简为x2-3x+2=0D化简为4x2-1=4x2+12x+9让学生上台解题教师进行点评讲解教师强调要找到个项系数要化成一般形式,系数和项均包含前面的符号 加深对概念的理解。以学生为主体是教学的基本出发点是新课改的素质教育,发挥学生主体作用。让部分学生上台写答案,师生再进行评价,教师可以及时发现问题,并且告诉学生二次项系数为正的更好。
巩固练习 例1.下列哪些是一元二次方程3x+2=5x-2 错x2=0对(x+3)(2x-4)=x2对x2=x3+x2-1错例2.填表例3.若x=3是方程x2+kx=0的一个根,试求常数k的值?x +kx=03 +3k=03k=-9k=-3 学生独立完成,老师巡视指导,出现问题是及时更正 在课堂上回顾知识,有不懂的问题可以及时询问老师,加强知识的巩固,并且了解学生的学习情况。
课堂小结 让学生总结本节课学了哪些知识,应该注意什么? 让学生对本节课的知识有一个结构的梳理,清晰知识的结构,有助于学知识的记忆。培养学生归纳概括的能力。
课后作业 必做:易:课本P4第1题1、2、4、6中:课本P4第5、6题难:课本P4第7题选做:请同学们了解一元二次方程的由来,并写出自己在这节课的收获感想。 老师布置学生按规定时间完成 课后作业对本节知识进行巩固和提高。布置分层作业尊重学生的个体差异,可以使同学们在原有的基础上提高,激发学生学习的积极性。对于难度较大的作业可以提高学生的能力。
板书设计
1
同课章节目录
