24.1 圆的相关性质 学案(无答案)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 24.1 圆的相关性质 学案(无答案)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 00:00:00 | ||
图片预览


文档简介
圆的相关性质
一、知识点
模块一 圆的基本概念
定 义 示例剖析
圆:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆. 固定的端点O叫做圆心,线段OA叫做半径. 由圆的定义可知: (1)圆上的各点到圆心的距离都等于半径长;在一个平面内,到圆心的距离等于半径长的点都在同一个圆上.因此,圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形. (2)要确定一个圆,需要两个基本条件,一个是圆心的位置,另一个是半径的长短,其中,圆心确定圆的位置,半径长确定圆的大小. 表示为“”
圆心相同且半径相等的圆叫做同圆; 圆心相同,半径不相等的两个圆叫做同心圆; 能够重合的两个圆叫做等圆.
弦和弧: 1.连接圆上任意两点的线段叫做弦.经过圆心的弦叫做直径,并且直径是同一圆中最长的弦,直径等于半径的2倍. 2.圆上任意两点间的部分叫做圆弧,简称弧. 以A、B为端点的弧记作,读作弧AB. 在同圆或等圆中,能够互相重合的弧叫做等弧. 3.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆. 4.在一个圆中大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧. 表示:劣弧 优弧或
圆心角和圆周角: 1.顶点在圆心的角叫做圆心角. 2.顶点在圆上,并且两边都和圆相交的角叫做圆周角.
模块二 垂径定理
1.圆的对称性
圆是轴对称图形,也是中心对称图形,其对称轴是任意一条过原点的直线,对称中心是圆心.
2.垂径定理
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
注意:垂径定理中的五个元素——“过圆心”、“垂直弦”、“平分弦”、“平分优弧”、“平分劣弧”,构成知二推三.
模块三 圆周角定理
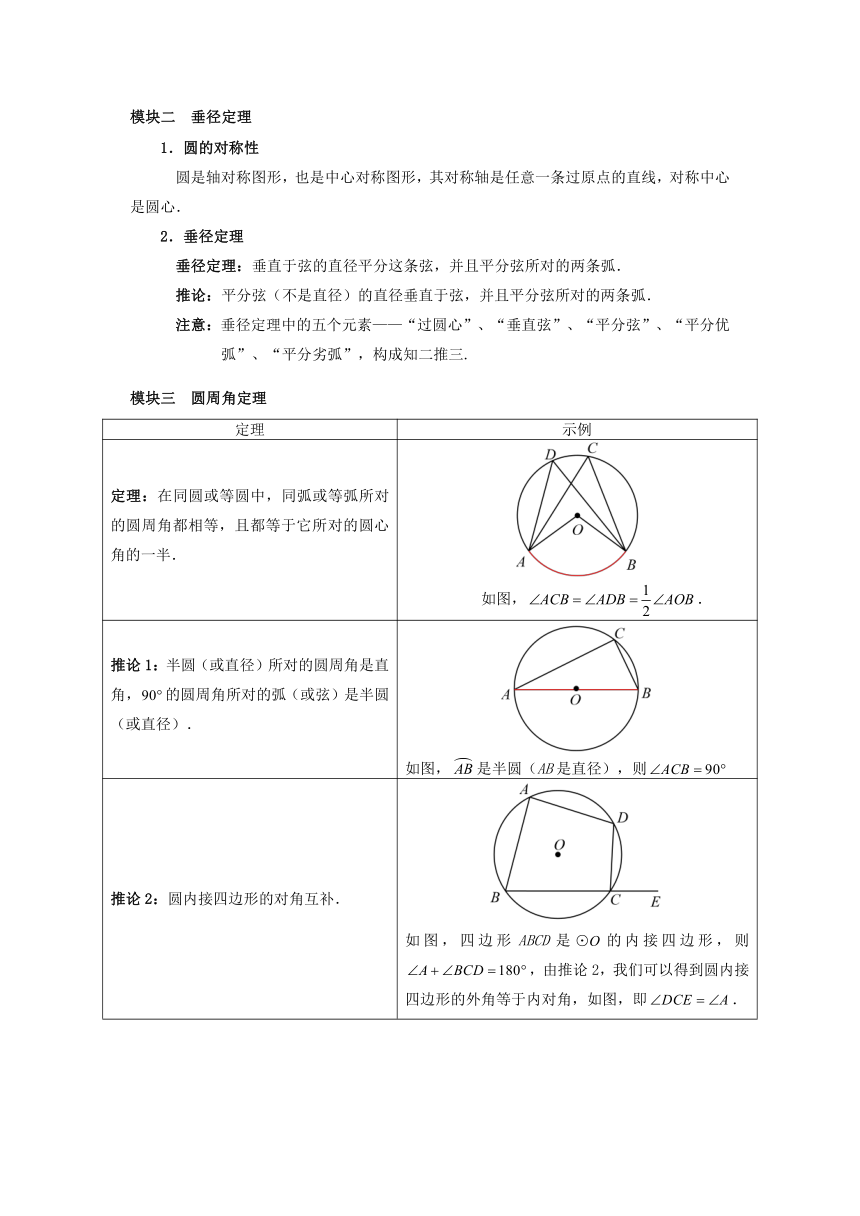
定理 示例
定理:在同圆或等圆中,同弧或等弧所对的圆周角都相等,且都等于它所对的圆心角的一半. 如图,.
推论1:半圆(或直径)所对的圆周角是直角,的圆周角所对的弧(或弦)是半圆(或直径). 如图,是半圆(AB是直径),则
推论2:圆内接四边形的对角互补. 如图,四边形ABCD是的内接四边形,则,由推论2,我们可以得到圆内接四边形的外角等于内对角,如图,即.
二、精讲精练
例1.下列说法错误的是( )
A.直径是圆中最长的弦 B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆 D.半径相等的两个半圆是等弧
【变式练习】
1.下列说法正确的是( )
A.长度相等的两条弧是等弧 B.优弧一定大于劣弧
C.不同的圆中不可能有相等的弦 D.直径是弦且同一个圆中最长的弦
例2.如图,已知AB是⊙O的直径,∠AOE=60°,点C是AB延长线上一点,CE交⊙O于点D,且CD=OB,则∠C等于( )
A.10° B.15° C.20° D.30°
【变式练习】
2.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD=( )
A.10° B.15° C.20° D.25°
例3.直线与 O相交于A、B两点,若 O的直径为26cm,圆心O到的距离是12cm,则线段AB的长是 .
【变式练习】
3.如图,某下水道的横截面是圆形的,水面CD的宽度为2m,F是线段CD的中点, EF经过圆心O交⊙O与点E,EF=3m,则⊙O直径的长是( )
A.m B.m C.m D.m
例4.如图,AB是⊙O的直径,C、D是⊙O上的两点,∠AOC=120°,
则∠CDB= °.
【变式练习】
4.如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD、BD.
(1)求弦AB的长;
(2)当∠ADC=15°时,求弦BD的长.
沙场点兵,磨刀霍霍
1.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
2.如图,在⊙O中,=2,则以下数量关系正确的是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
3.如图,AB为⊙O直径,弦CD⊥AB于E,则下面结论中错误的是( )
A.CE=DE B.= C.∠BAC=∠BAD D.OE=BE
4.如图,∠AOB=100°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为 ( )
A.50° B.80°或50°
C.130° D. 50°或130°
5.如图,AB是⊙O的直径,点D是弧的中点,∠ABC=52°,则∠DAB等于( )
A.58° B.61° C.72° D.64°
6.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是 ( )
A.50° B.60°
C.80° D.100°
7.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m B.24m C.30m D.60m
8.如图,点A、B、C在⊙O上,点D是AB延长线上一点,若∠CBD=55°,则∠AOC的度数为( )
A.100° B.105° C.110° D.125°
9.如图,已知∠OBA=20°,且OC=AC,则∠BOC的度数是( )
A.70° B.80° C.40° D.60°
10.(2020 麻城市校级模拟)如图,⊙O的半径为6,AB为弦,点C为的中点,若∠ABC=30°,则弦AB的长为( )
A. B.6 C. D.
12. O中平行弦AB、CD的长分别为6cm,8cm, O的半径为5cm,求AB与CD间的距离__________.
13.一点到圆的最远距离为9cm,最近距离为4cm,则该圆的半径为 .
14..若M为 O内一点,0M=3,圆O半径为4,则圆O中过点M的最短的弦长为 .
15.如图,在△ABC中,已知∠ACB=130°, ∠BAC=20°,BC =2,以点C为圆心.CB为半径的圆交AB于点D.则BD的长为 .
16.如果四边形中的四个顶点都在圆上,并且,则x的值为 .
17.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为_________________.
18.如图,AB是⊙O的直径,C、D为⊙O上的点,且AD平分∠CAB,作DE⊥AB于点E.
(1)求证:AC∥OD;
(2)若OE=4,求AC的长.
19.如图,BE是⊙O的直径,半径OA⊥弦BC,垂足为D,连接AE、EC.
(1)若∠AEC=25°,求∠AOB的度数;
(2)若∠A=∠B,EC=4,求⊙O的半径.
20.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=40°,求∠BAD的度数;
(2)求证:∠1=∠2.
21.(广州市)如图,⊙O的直径AB=10,弦AC=8,连接BC.
(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)
(2)在(1)所作的图中,求四边形ABCD的周长.
一、知识点
模块一 圆的基本概念
定 义 示例剖析
圆:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆. 固定的端点O叫做圆心,线段OA叫做半径. 由圆的定义可知: (1)圆上的各点到圆心的距离都等于半径长;在一个平面内,到圆心的距离等于半径长的点都在同一个圆上.因此,圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形. (2)要确定一个圆,需要两个基本条件,一个是圆心的位置,另一个是半径的长短,其中,圆心确定圆的位置,半径长确定圆的大小. 表示为“”
圆心相同且半径相等的圆叫做同圆; 圆心相同,半径不相等的两个圆叫做同心圆; 能够重合的两个圆叫做等圆.
弦和弧: 1.连接圆上任意两点的线段叫做弦.经过圆心的弦叫做直径,并且直径是同一圆中最长的弦,直径等于半径的2倍. 2.圆上任意两点间的部分叫做圆弧,简称弧. 以A、B为端点的弧记作,读作弧AB. 在同圆或等圆中,能够互相重合的弧叫做等弧. 3.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆. 4.在一个圆中大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧. 表示:劣弧 优弧或
圆心角和圆周角: 1.顶点在圆心的角叫做圆心角. 2.顶点在圆上,并且两边都和圆相交的角叫做圆周角.
模块二 垂径定理
1.圆的对称性
圆是轴对称图形,也是中心对称图形,其对称轴是任意一条过原点的直线,对称中心是圆心.
2.垂径定理
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
注意:垂径定理中的五个元素——“过圆心”、“垂直弦”、“平分弦”、“平分优弧”、“平分劣弧”,构成知二推三.
模块三 圆周角定理
定理 示例
定理:在同圆或等圆中,同弧或等弧所对的圆周角都相等,且都等于它所对的圆心角的一半. 如图,.
推论1:半圆(或直径)所对的圆周角是直角,的圆周角所对的弧(或弦)是半圆(或直径). 如图,是半圆(AB是直径),则
推论2:圆内接四边形的对角互补. 如图,四边形ABCD是的内接四边形,则,由推论2,我们可以得到圆内接四边形的外角等于内对角,如图,即.
二、精讲精练
例1.下列说法错误的是( )
A.直径是圆中最长的弦 B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆 D.半径相等的两个半圆是等弧
【变式练习】
1.下列说法正确的是( )
A.长度相等的两条弧是等弧 B.优弧一定大于劣弧
C.不同的圆中不可能有相等的弦 D.直径是弦且同一个圆中最长的弦
例2.如图,已知AB是⊙O的直径,∠AOE=60°,点C是AB延长线上一点,CE交⊙O于点D,且CD=OB,则∠C等于( )
A.10° B.15° C.20° D.30°
【变式练习】
2.如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,连接CD,则∠ACD=( )
A.10° B.15° C.20° D.25°
例3.直线与 O相交于A、B两点,若 O的直径为26cm,圆心O到的距离是12cm,则线段AB的长是 .
【变式练习】
3.如图,某下水道的横截面是圆形的,水面CD的宽度为2m,F是线段CD的中点, EF经过圆心O交⊙O与点E,EF=3m,则⊙O直径的长是( )
A.m B.m C.m D.m
例4.如图,AB是⊙O的直径,C、D是⊙O上的两点,∠AOC=120°,
则∠CDB= °.
【变式练习】
4.如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD、BD.
(1)求弦AB的长;
(2)当∠ADC=15°时,求弦BD的长.
沙场点兵,磨刀霍霍
1.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
2.如图,在⊙O中,=2,则以下数量关系正确的是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
3.如图,AB为⊙O直径,弦CD⊥AB于E,则下面结论中错误的是( )
A.CE=DE B.= C.∠BAC=∠BAD D.OE=BE
4.如图,∠AOB=100°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为 ( )
A.50° B.80°或50°
C.130° D. 50°或130°
5.如图,AB是⊙O的直径,点D是弧的中点,∠ABC=52°,则∠DAB等于( )
A.58° B.61° C.72° D.64°
6.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是 ( )
A.50° B.60°
C.80° D.100°
7.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m B.24m C.30m D.60m
8.如图,点A、B、C在⊙O上,点D是AB延长线上一点,若∠CBD=55°,则∠AOC的度数为( )
A.100° B.105° C.110° D.125°
9.如图,已知∠OBA=20°,且OC=AC,则∠BOC的度数是( )
A.70° B.80° C.40° D.60°
10.(2020 麻城市校级模拟)如图,⊙O的半径为6,AB为弦,点C为的中点,若∠ABC=30°,则弦AB的长为( )
A. B.6 C. D.
12. O中平行弦AB、CD的长分别为6cm,8cm, O的半径为5cm,求AB与CD间的距离__________.
13.一点到圆的最远距离为9cm,最近距离为4cm,则该圆的半径为 .
14..若M为 O内一点,0M=3,圆O半径为4,则圆O中过点M的最短的弦长为 .
15.如图,在△ABC中,已知∠ACB=130°, ∠BAC=20°,BC =2,以点C为圆心.CB为半径的圆交AB于点D.则BD的长为 .
16.如果四边形中的四个顶点都在圆上,并且,则x的值为 .
17.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为_________________.
18.如图,AB是⊙O的直径,C、D为⊙O上的点,且AD平分∠CAB,作DE⊥AB于点E.
(1)求证:AC∥OD;
(2)若OE=4,求AC的长.
19.如图,BE是⊙O的直径,半径OA⊥弦BC,垂足为D,连接AE、EC.
(1)若∠AEC=25°,求∠AOB的度数;
(2)若∠A=∠B,EC=4,求⊙O的半径.
20.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=40°,求∠BAD的度数;
(2)求证:∠1=∠2.
21.(广州市)如图,⊙O的直径AB=10,弦AC=8,连接BC.
(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)
(2)在(1)所作的图中,求四边形ABCD的周长.
同课章节目录
