24.2.2 直线和圆的位置关系 切线长定理 同步练习(无答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 切线长定理 同步练习(无答案) 2023—2024学年人教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 206.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 00:00:00 | ||
图片预览

文档简介
24.2.2 直线和圆的位置关系——切线长定理
一、选择题:
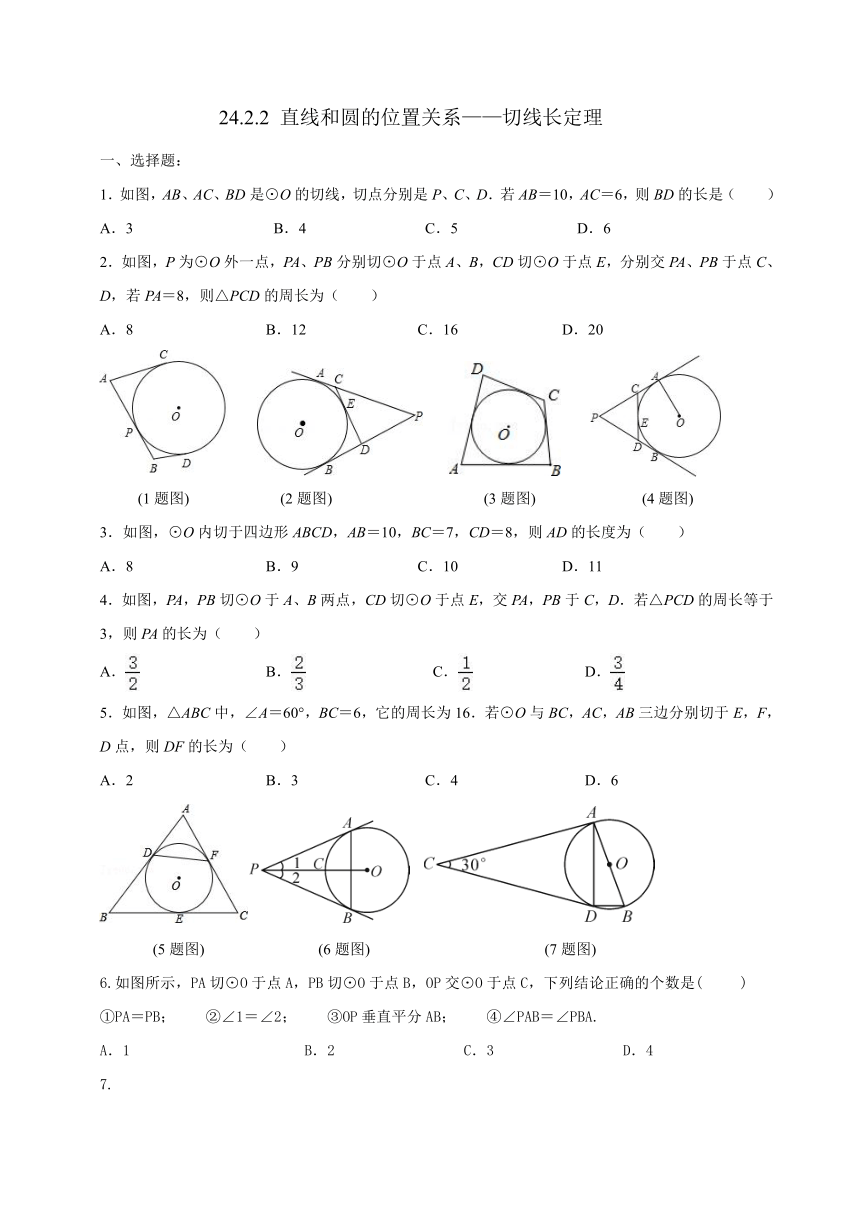
1.如图,AB、AC、BD是⊙O的切线,切点分别是P、C、D.若AB=10,AC=6,则BD的长是( )
A.3 B.4 C.5 D.6
2.如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=8,则△PCD的周长为( )
A.8 B.12 C.16 D.20
(1题图) (2题图) (3题图) (4题图)
3.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
4.如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的长为( )
A. B. C. D.
5.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,
D点,则DF的长为( )
A.2 B.3 C.4 D.6
(5题图) (6题图) (7题图)
6.如图所示,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论正确的个数是( )
①PA=PB; ②∠1=∠2; ③OP垂直平分AB; ④∠PAB=∠PBA.
A.1 B.2 C.3 D.4
7.
如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
A.15° B.30° C.60° D.75
二、填空题:
8.已知△ABC的周长为24,若△ABC的内切圆半径为2,则△ABC的面积为____.
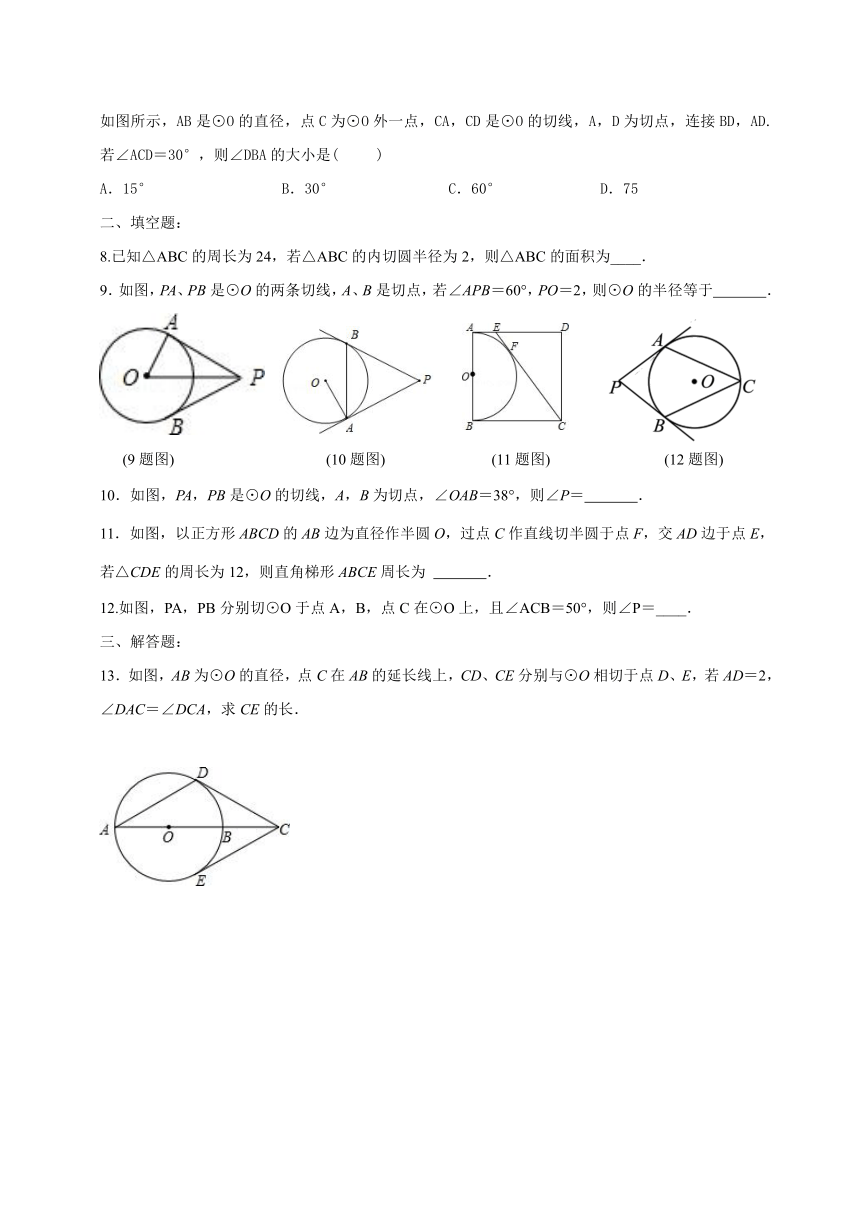
9.如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于 .
(9题图) (10题图) (11题图) (12题图)
10.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P= .
11.如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE周长为 .
12.如图,PA,PB分别切⊙O于点A,B,点C在⊙O上,且∠ACB=50°,则∠P=____.
三、解答题:
13.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,求CE的长.
14.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
15.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.
求:(1)PA的长;(2)∠COD的度数.
如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=28 cm,CA=26 cm,求AF,BD,CE的长.
17.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,求∠CPD.
18.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,AC,PB的延长线相交于点D.
(1)若∠1=20°,求∠APB的度数;
(2)当∠1为多少度时,OP=OD?并说明理由.
一、选择题:
1.如图,AB、AC、BD是⊙O的切线,切点分别是P、C、D.若AB=10,AC=6,则BD的长是( )
A.3 B.4 C.5 D.6
2.如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=8,则△PCD的周长为( )
A.8 B.12 C.16 D.20
(1题图) (2题图) (3题图) (4题图)
3.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( )
A.8 B.9 C.10 D.11
4.如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的长为( )
A. B. C. D.
5.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,
D点,则DF的长为( )
A.2 B.3 C.4 D.6
(5题图) (6题图) (7题图)
6.如图所示,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论正确的个数是( )
①PA=PB; ②∠1=∠2; ③OP垂直平分AB; ④∠PAB=∠PBA.
A.1 B.2 C.3 D.4
7.
如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
A.15° B.30° C.60° D.75
二、填空题:
8.已知△ABC的周长为24,若△ABC的内切圆半径为2,则△ABC的面积为____.
9.如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于 .
(9题图) (10题图) (11题图) (12题图)
10.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P= .
11.如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AD边于点E,若△CDE的周长为12,则直角梯形ABCE周长为 .
12.如图,PA,PB分别切⊙O于点A,B,点C在⊙O上,且∠ACB=50°,则∠P=____.
三、解答题:
13.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,求CE的长.
14.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P的度数.
15.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.
求:(1)PA的长;(2)∠COD的度数.
如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=28 cm,CA=26 cm,求AF,BD,CE的长.
17.如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,求∠CPD.
18.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,AC,PB的延长线相交于点D.
(1)若∠1=20°,求∠APB的度数;
(2)当∠1为多少度时,OP=OD?并说明理由.
同课章节目录
