12.3 角的平分线的性质同步练习(无答案)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 12.3 角的平分线的性质同步练习(无答案)2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 215.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 17:31:46 | ||
图片预览


文档简介
人教版八年级上12.3 角的平分线的性质
一、选择题
1. 如图,Rt△ABC中,∠C=90°,BG平分∠ABC,交AC于点G,若CG=1,P为AB上一动点,则GP的最小值为( )
A.1 B. C.2 D.无法确定
2. 如图,在中,,AD是的角平分线,,,则的面积为( )
A.30 B.18 C.15 D.9
3. 下列命题中,是假命题的是( )
A.对顶角相等 B.同旁内角相等
C.全等三角形的对应边相等 D.角平分线上的点到这个角的两边的距离相等
4. 下列命题是真命题的是( )
A.面积相等的两个三角形全等
B.两条直线被第三条直线所截同位角相等
C.角平分线上的点到两边的距离相等
D.同旁内角互补
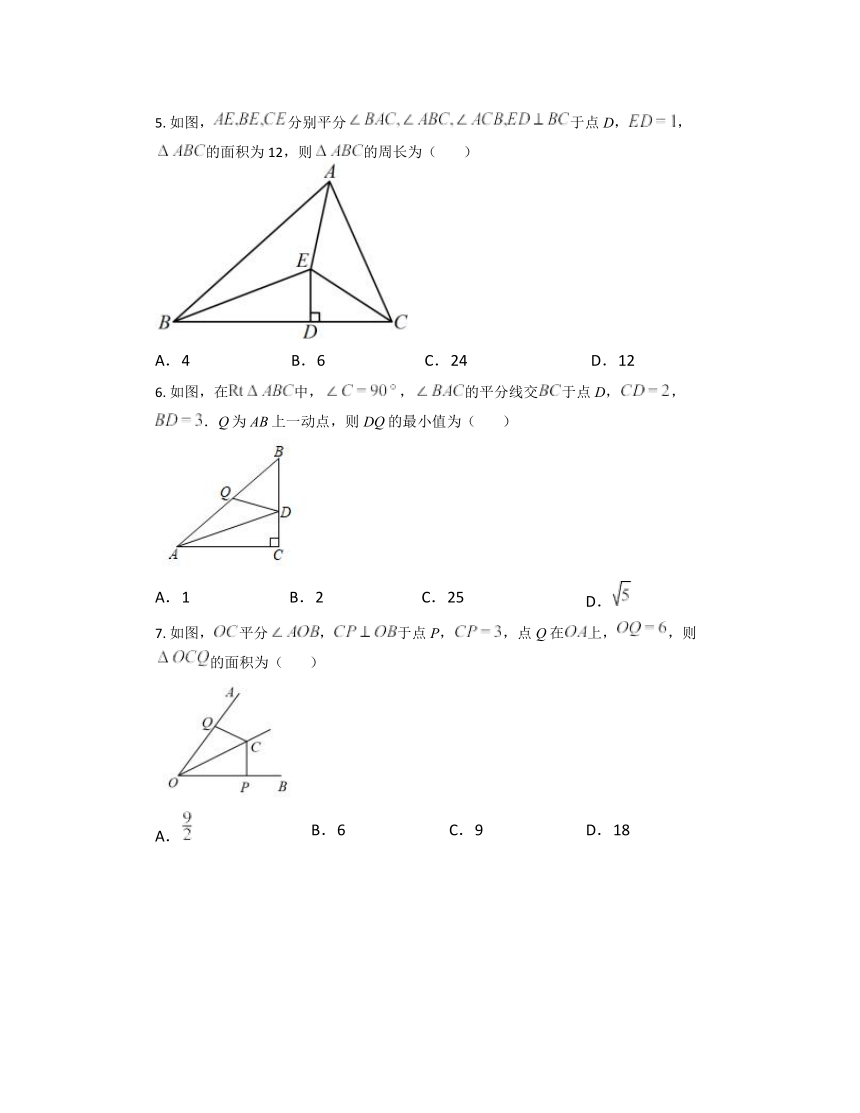
5. 如图,分别平分于点D,,的面积为12,则的周长为( )
A.4 B.6 C.24 D.12
6. 如图,在中,,的平分线交于点D,,.Q为AB上一动点,则DQ的最小值为( )
A.1 B.2 C.25 D.
7. 如图,平分,于点P,,点Q在上,,则的面积为( )
A. B.6 C.9 D.18
8. 如图,平分.于,于,则与的大小关系( ).
A.不能确定 B. C. D.
9. 如图,射线是的角平分线,是射线上一点,于点,,若点Q是射线上一点,,则的面积是( )
A.10 B.5 C.15 D.20
10. 如图,中,,利用尺规在上分别截取,使;分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线交于点G.若,P为上一动点,则的最小值为( )
A.无法确定 B. C.1 D.2
11. 如图,在中,.按以下步骤作图:①以B为圆心,任意长为半径作弧,交于点M,交于点N;②分别以M,N为圆心,以大于的长为半径作弧,两弧相交于点P;③作射线,交边于点D,点E是
边上一动点,连接.若,则线段的最小值是( )
A. B.3 C. D.2
二、填空题
12. 如图,在Rt△OCD中,∠C=90°,OP平分∠DOC交DC于点P,若PC=2,OD=8,则△OPD的面积为_____.
13. 如图,BD是△ABC的角平分线,DE⊥BC,垂足为E. △ABC的面积为35,AB=8.BC=6,则DE=__________.
14. 如图,任意画一个∠BAC=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AD=AE;④PD=PE;⑤BD+CE=BC;其中正确的结论为__________
.(填写序号)
15. 如图,在中,点是上的一点,已知,,平分交于点,连接,则________度.
三、解答题
16. 直线l1,l2,l3表示三条相互交叉的公路,现在拟建一个货物中转站,要求它到三条公路的距离都相等,请画出符合要求的地址(保持作图痕迹,不要求写作法)
17. 如图,已知,利用尺规,在边上求作一点,使得.(保留作图痕迹,不写作法)
18. 如图,中,平分,且于E.
(1)求证:;
(2)如果,求的长.
19. 如图,是的角平分线,且,,.
(1)求的度数.
(2)若,点F是上的动点,求的最小值.
20. 如图,在中,,,是的一条角平分线.若,求的面积.
一、选择题
1. 如图,Rt△ABC中,∠C=90°,BG平分∠ABC,交AC于点G,若CG=1,P为AB上一动点,则GP的最小值为( )
A.1 B. C.2 D.无法确定
2. 如图,在中,,AD是的角平分线,,,则的面积为( )
A.30 B.18 C.15 D.9
3. 下列命题中,是假命题的是( )
A.对顶角相等 B.同旁内角相等
C.全等三角形的对应边相等 D.角平分线上的点到这个角的两边的距离相等
4. 下列命题是真命题的是( )
A.面积相等的两个三角形全等
B.两条直线被第三条直线所截同位角相等
C.角平分线上的点到两边的距离相等
D.同旁内角互补
5. 如图,分别平分于点D,,的面积为12,则的周长为( )
A.4 B.6 C.24 D.12
6. 如图,在中,,的平分线交于点D,,.Q为AB上一动点,则DQ的最小值为( )
A.1 B.2 C.25 D.
7. 如图,平分,于点P,,点Q在上,,则的面积为( )
A. B.6 C.9 D.18
8. 如图,平分.于,于,则与的大小关系( ).
A.不能确定 B. C. D.
9. 如图,射线是的角平分线,是射线上一点,于点,,若点Q是射线上一点,,则的面积是( )
A.10 B.5 C.15 D.20
10. 如图,中,,利用尺规在上分别截取,使;分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线交于点G.若,P为上一动点,则的最小值为( )
A.无法确定 B. C.1 D.2
11. 如图,在中,.按以下步骤作图:①以B为圆心,任意长为半径作弧,交于点M,交于点N;②分别以M,N为圆心,以大于的长为半径作弧,两弧相交于点P;③作射线,交边于点D,点E是
边上一动点,连接.若,则线段的最小值是( )
A. B.3 C. D.2
二、填空题
12. 如图,在Rt△OCD中,∠C=90°,OP平分∠DOC交DC于点P,若PC=2,OD=8,则△OPD的面积为_____.
13. 如图,BD是△ABC的角平分线,DE⊥BC,垂足为E. △ABC的面积为35,AB=8.BC=6,则DE=__________.
14. 如图,任意画一个∠BAC=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AD=AE;④PD=PE;⑤BD+CE=BC;其中正确的结论为__________
.(填写序号)
15. 如图,在中,点是上的一点,已知,,平分交于点,连接,则________度.
三、解答题
16. 直线l1,l2,l3表示三条相互交叉的公路,现在拟建一个货物中转站,要求它到三条公路的距离都相等,请画出符合要求的地址(保持作图痕迹,不要求写作法)
17. 如图,已知,利用尺规,在边上求作一点,使得.(保留作图痕迹,不写作法)
18. 如图,中,平分,且于E.
(1)求证:;
(2)如果,求的长.
19. 如图,是的角平分线,且,,.
(1)求的度数.
(2)若,点F是上的动点,求的最小值.
20. 如图,在中,,,是的一条角平分线.若,求的面积.
