5.1 相交线同步练习(含解析)
文档属性
| 名称 | 5.1 相交线同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 453.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.1相交线华师大版初中数学七年级上册同步练习
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.关于两条直线相交所成的四个角,下列说法中,正确的是( )
A. 至少有两个锐角 B. 至少有两个钝角
C. 至少有两个直角 D. 至少有两个不是钝角
2.下列四个图形中,与是内错角的是( )
A. B. C. D.
3.如图,直线、相交于点,,根据图中的尺规作图痕迹,则的度数是( )
A.
B.
C.
D.
4.如图,在直角三角形中,,,,,则点到的距离是( )
A.
B.
C.
D.
5.下列各选项中能用“垂线段最短”来解释的现象是( )
A. 测量跳远成绩
B. 木板上弹墨线
C. 两钉子固定木条
D. 弯曲河道改直
6.将含角的直角三角板按如图所示放置到一组平行线中,若,则等于( )
A.
B.
C.
D.
7.如图所示,计划在河边的,,,处,引水到处,从何处引水,能使所用的水管最短( )
A. 处
B. 处
C. 处
D. 处
8.,两村庄分别在一条公路的两侧,到的距离为公里,到的距离为公里,,相距公里,欲在公路某处建一个垃圾站,使得,两个村庄到此处处理垃圾都比较方便,应建在离公里处.( )
A. B. C. D.
9.两条直线最多有一个交点,三条直线最多有三个交点,四条直线最多有个交点,,那么条线段最多( )
A. 个交点 B. 个交点 C. 个交点 D. 个交点
10.如图,一副三角板的直角顶点重合,等腰三角板的腰于,则( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
11.如图,直线、相交于点,若::,的度数是______ .
12.在中,,,点为上一动点,,则的最小值是______ .
13.如图,三角形中,,边最长的依据是______ .
14.观察图形,并阅读相关的文字,回答:如有条直线相交,最多有交点______.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
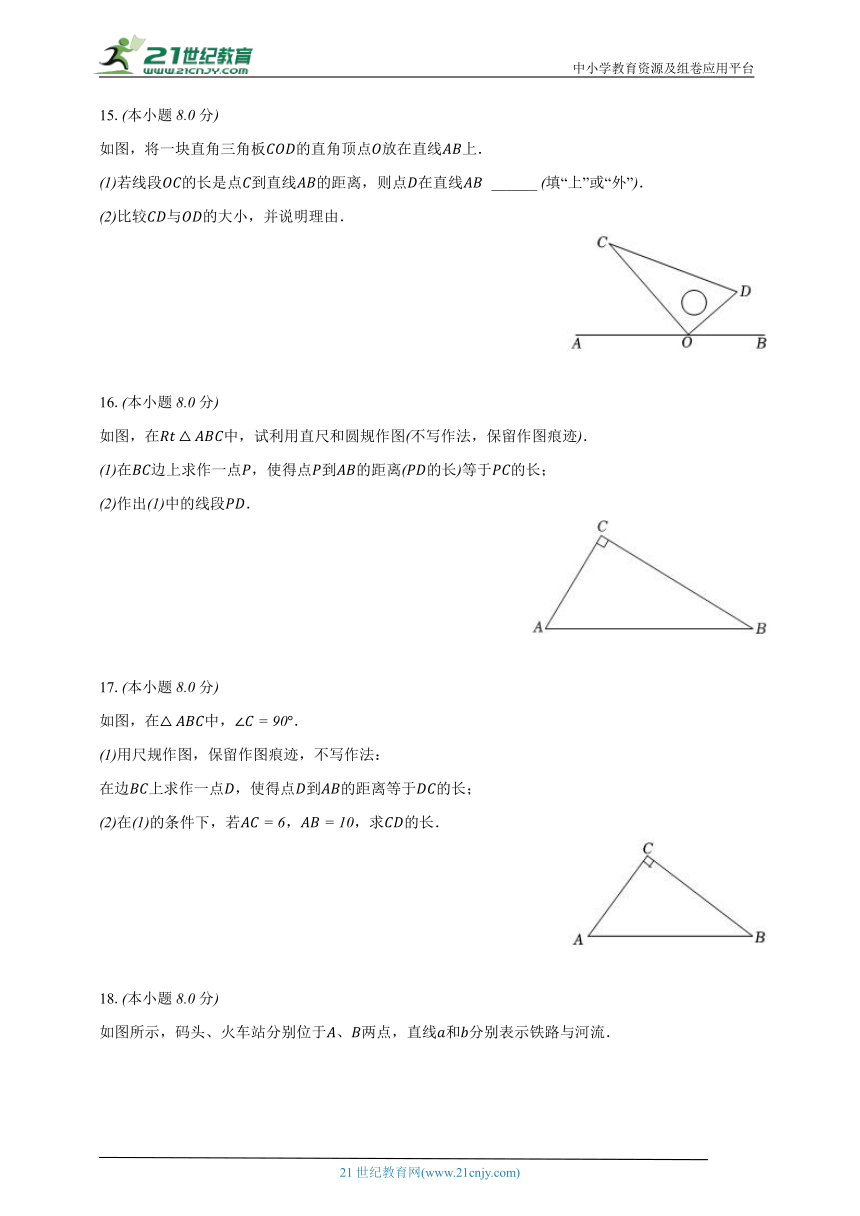
15.本小题分
如图,将一块直角三角板的直角顶点放在直线上.
若线段的长是点到直线的距离,则点在直线 ______ 填“上”或“外”.
比较与的大小,并说明理由.
16.本小题分
如图,在中,试利用直尺和圆规作图不写作法,保留作图痕迹.
在边上求作一点,使得点到的距离的长等于的长;
作出中的线段.
17.本小题分
如图,在中,.
用尺规作图,保留作图痕迹,不写作法:
在边上求作一点,使得点到的距离等于的长;
在的条件下,若,,求的长.
18.本小题分
如图所示,码头、火车站分别位于、两点,直线和分别表示铁路与河流.
从火车站到码头怎样走最近画图并说明理由.
从码头到铁路怎样走最近画图并说明理由.
从火车站到河流怎样走最近画图并说明理由.
19.本小题分
如图,是直线上一点,以点为端点作射线,使得,射线不动,射线,同时开始绕点顺时针转动一周.
若射线,的转动速度相同,均为每秒,则当时,转动的时间为 当时,转动的时间为
若射线,的转动速度分别为每秒和每秒,则当时,转动的时间为多少
20.本小题分
如图,直线,相交于点,.
若,,求的度数.
如果,那么与互相垂直吗请说明理由.
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】解:、与是同位角,选项错误,不符合题意;
B、与是同旁内角,选项错误,不符合题意;
C、与不是内错角,选项错误,不符合题意;
D、与是内错角,选项正确,符合题意;
故选:.
根据内错角的概念判断即可.
此题考查内错角,关键是根据内错角的概念解答.
3.【答案】
【解析】解:由作图痕迹得平分,,
,,
,
,
.
故选:.
利用基本作图得到平分,,所以,,再根据对顶角相等得到,所以,然后计算即可.
本题考查了作图基本作图:熟练掌握种基本作图是解决问题的关键.也考查了对顶角、邻补角.
4.【答案】
【解析】解:在直角三角形中,,
,
,,,
,
,
故选:.
根据面积相等即可求出点到的距离.
本题考查点到直线的距离,求直角三角形斜边上的高,用面积法列出关系式是解题关键.
5.【答案】
【解析】解:、测量跳远成绩是利用了“垂线段最短”,故本选项合题意.
B、木板弹出一条墨迹是利用了“两点确定一条直线”,故本选项不合题意;
C、用两个钉子就可以把木条固定在墙上是利用了“两点确定一条直线”,故本选项不合题意;
D、把弯曲的河道改直,就能缩短路程是利用了“两点之间,线段最短”,故本选项不符合题意;
故选:.
根据直线的性质,线段的性质对各选项分析判断即可得解.
本题考查了线段的性质,直线的性质,解题时注意:两点的所有连线中可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.
6.【答案】
【解析】解:如图,
直线,
.
,
.
故选:.
由直线,利用“两直线平行,同位角相等”可求出的度数,在中利用三角形内角和定理可求出的度数,再利用三角形外角的性质可求出的度数,结合对顶角相等即可得出的度数.
本题考查了平行线的性质、三角形内角和定理以及三角形外角的性质,利用平行线的性质及三角形外角的性质,求出的度数是解题的关键.
7.【答案】
【解析】解:,
由垂线段最短可知,从处引水,能使所用的水管最短.
故选:.
根据垂线段的性质:垂线段最短,可得答案.
本题考查了垂线段的性质,熟记性质是解题关键.
8.【答案】
【解析】解:设应建在离处公里的处.
使得,两个村庄到此处处理垃圾都比较方便,
,
公里,公里,
公里,如图:
在中,公里,公里,
由勾股定理得:,
在中,公里,公里,
由勾股定理得:,
,
,
,
解得:.
应建在离公里处.
故选:.
根据“使得,两个村庄到此处处理垃圾都比较方便”可知选取的地点距,两地的距离相等,设应建在离处公里的处,则,然后利用勾股定理构造关于的方程,然后解方程求出即可.
此题主要考查了勾股定理的实际应用,根据题意画出示意图,理解“使得,两个村庄到此处处理垃圾都比较方便”的含义,灵活运用勾股定理构造方程是答此题的关键.
9.【答案】
【解析】【分析】
此题主要考查了图形变化类,此题在相交线的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊向一般猜想的方法.
根据题意,结合图形,发现:条直线相交最多有个交点,条直线相交最多有个交点,条直线相交最多有个交点,故可猜想,条直线相交,最多有个交点.
【解答】
解:条直线相交最多有个交点,条直线相交最多有个交点,条直线相交最多有个交点,而,,,
七条直线相交最多有交点的个数是:.
故选:.
10.【答案】
【解析】解:,
,
,
,
,
.
故选:.
根据三角板的特点和三角形外角的性质求解即可.
此题考查了两个直角三角板角度的特点,三角形外角的性质,解题的关键是熟练掌握以上知识点.
11.【答案】
【解析】解:,
,
::,,
,
,
.
故答案为:.
根据已知条件求出,再根据对顶角相等求出,再利用即可求出结果.
本题考查了垂线,对顶角的定义和角的和差计算,熟练掌握对顶角的定义是解题的关键.
12.【答案】
【解析】解:根据点到直线垂线段最短,当时,最短.
设,则,
在中,,
,
,
在中,,由勾股定理得,
,即;
解得,
.
故答案为:.
根据点到直线垂线段最短,当时,最短,计算垂线段长即可.
本题考查了垂线段最短,熟练掌握勾股定理计算边长是解答本题的关键.
13.【答案】垂线段最短
【解析】解:,点到的距离是线段的长,故AC,
点到的距离是线段的长,故BC,
所以边最长,依据为垂线段最短,
故答案为:垂线段最短.
结合图形和已知条件,根据点到直线的距离的定义和垂线段最短求解.
本题考查了点到直线的距离的定义以及垂线段最短的性质,解题的关键是熟练掌握相关基础知识.
14.【答案】
【解析】【分析】
此题主要考查了相交线,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊向一般猜想的方法.
根据题意,结合图形可猜想,条直线相交,最多有个交点.
【解答】
解:条直线相交最多有个交点,条直线相交最多有个交点,条直线相交最多有个交点,
而,,,
条直线相交,最多有个交点,
当时,.
故答案为.
15.【答案】上
【解析】解:线段的长是点到直线的距离,
,
,
,重合,
则点在直线上.
,理由如下:
,
与上各点的连线段中,垂线段最短.
.
由线段的长是点到直线的距离,可得,结合,从而可得答案;
由垂线段最短可得答案.
本题考查的是点到直线的距离,垂线段最短,熟记点到直线的距离的含义是解本题的关键.
16.【答案】解:如图,点即为所求;
如图,线段即为所求.
【解析】由点到的距离的长等于的长知点在平分线上,再根据角平分线的尺规作图即可得;
根据过直线外一点作已知直线的垂线的尺规作图即可得.
本题考查作图复杂作图、角平分线的性质定理等知识,解题的关键是熟练掌握基本作图,灵活运用所学知识解决问题,属于中考常考题型.
17.【答案】解:如图,点即为所求;
过点作于点.
由作图可知平分,,,
,
,,,
,
,
,
,
.
【解析】作射线平分交于点,点即为所求;
过点作于点利用面积法求解即可.
本题考查作图复杂作图,角平分线的性质定理,三角形的面积等知识,解题的关键是学会利用面积法解决问题.
18.【答案】【小题】
如图所示沿走最近理由:两点之间线段最短.
【小题】
如图所示沿走最近理由:垂线段最短.
【小题】
如图所示沿走最近理由:垂线段最短.
【解析】 略
略
略
19.【答案】【小题】
或
或
【小题】
或
【解析】 略
略
20.【答案】【小题】
,.,.,.
【小题】
理由如下:,,,即,.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1相交线华师大版初中数学七年级上册同步练习
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.关于两条直线相交所成的四个角,下列说法中,正确的是( )
A. 至少有两个锐角 B. 至少有两个钝角
C. 至少有两个直角 D. 至少有两个不是钝角
2.下列四个图形中,与是内错角的是( )
A. B. C. D.
3.如图,直线、相交于点,,根据图中的尺规作图痕迹,则的度数是( )
A.
B.
C.
D.
4.如图,在直角三角形中,,,,,则点到的距离是( )
A.
B.
C.
D.
5.下列各选项中能用“垂线段最短”来解释的现象是( )
A. 测量跳远成绩
B. 木板上弹墨线
C. 两钉子固定木条
D. 弯曲河道改直
6.将含角的直角三角板按如图所示放置到一组平行线中,若,则等于( )
A.
B.
C.
D.
7.如图所示,计划在河边的,,,处,引水到处,从何处引水,能使所用的水管最短( )
A. 处
B. 处
C. 处
D. 处
8.,两村庄分别在一条公路的两侧,到的距离为公里,到的距离为公里,,相距公里,欲在公路某处建一个垃圾站,使得,两个村庄到此处处理垃圾都比较方便,应建在离公里处.( )
A. B. C. D.
9.两条直线最多有一个交点,三条直线最多有三个交点,四条直线最多有个交点,,那么条线段最多( )
A. 个交点 B. 个交点 C. 个交点 D. 个交点
10.如图,一副三角板的直角顶点重合,等腰三角板的腰于,则( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
11.如图,直线、相交于点,若::,的度数是______ .
12.在中,,,点为上一动点,,则的最小值是______ .
13.如图,三角形中,,边最长的依据是______ .
14.观察图形,并阅读相关的文字,回答:如有条直线相交,最多有交点______.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
15.本小题分
如图,将一块直角三角板的直角顶点放在直线上.
若线段的长是点到直线的距离,则点在直线 ______ 填“上”或“外”.
比较与的大小,并说明理由.
16.本小题分
如图,在中,试利用直尺和圆规作图不写作法,保留作图痕迹.
在边上求作一点,使得点到的距离的长等于的长;
作出中的线段.
17.本小题分
如图,在中,.
用尺规作图,保留作图痕迹,不写作法:
在边上求作一点,使得点到的距离等于的长;
在的条件下,若,,求的长.
18.本小题分
如图所示,码头、火车站分别位于、两点,直线和分别表示铁路与河流.
从火车站到码头怎样走最近画图并说明理由.
从码头到铁路怎样走最近画图并说明理由.
从火车站到河流怎样走最近画图并说明理由.
19.本小题分
如图,是直线上一点,以点为端点作射线,使得,射线不动,射线,同时开始绕点顺时针转动一周.
若射线,的转动速度相同,均为每秒,则当时,转动的时间为 当时,转动的时间为
若射线,的转动速度分别为每秒和每秒,则当时,转动的时间为多少
20.本小题分
如图,直线,相交于点,.
若,,求的度数.
如果,那么与互相垂直吗请说明理由.
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】解:、与是同位角,选项错误,不符合题意;
B、与是同旁内角,选项错误,不符合题意;
C、与不是内错角,选项错误,不符合题意;
D、与是内错角,选项正确,符合题意;
故选:.
根据内错角的概念判断即可.
此题考查内错角,关键是根据内错角的概念解答.
3.【答案】
【解析】解:由作图痕迹得平分,,
,,
,
,
.
故选:.
利用基本作图得到平分,,所以,,再根据对顶角相等得到,所以,然后计算即可.
本题考查了作图基本作图:熟练掌握种基本作图是解决问题的关键.也考查了对顶角、邻补角.
4.【答案】
【解析】解:在直角三角形中,,
,
,,,
,
,
故选:.
根据面积相等即可求出点到的距离.
本题考查点到直线的距离,求直角三角形斜边上的高,用面积法列出关系式是解题关键.
5.【答案】
【解析】解:、测量跳远成绩是利用了“垂线段最短”,故本选项合题意.
B、木板弹出一条墨迹是利用了“两点确定一条直线”,故本选项不合题意;
C、用两个钉子就可以把木条固定在墙上是利用了“两点确定一条直线”,故本选项不合题意;
D、把弯曲的河道改直,就能缩短路程是利用了“两点之间,线段最短”,故本选项不符合题意;
故选:.
根据直线的性质,线段的性质对各选项分析判断即可得解.
本题考查了线段的性质,直线的性质,解题时注意:两点的所有连线中可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.
6.【答案】
【解析】解:如图,
直线,
.
,
.
故选:.
由直线,利用“两直线平行,同位角相等”可求出的度数,在中利用三角形内角和定理可求出的度数,再利用三角形外角的性质可求出的度数,结合对顶角相等即可得出的度数.
本题考查了平行线的性质、三角形内角和定理以及三角形外角的性质,利用平行线的性质及三角形外角的性质,求出的度数是解题的关键.
7.【答案】
【解析】解:,
由垂线段最短可知,从处引水,能使所用的水管最短.
故选:.
根据垂线段的性质:垂线段最短,可得答案.
本题考查了垂线段的性质,熟记性质是解题关键.
8.【答案】
【解析】解:设应建在离处公里的处.
使得,两个村庄到此处处理垃圾都比较方便,
,
公里,公里,
公里,如图:
在中,公里,公里,
由勾股定理得:,
在中,公里,公里,
由勾股定理得:,
,
,
,
解得:.
应建在离公里处.
故选:.
根据“使得,两个村庄到此处处理垃圾都比较方便”可知选取的地点距,两地的距离相等,设应建在离处公里的处,则,然后利用勾股定理构造关于的方程,然后解方程求出即可.
此题主要考查了勾股定理的实际应用,根据题意画出示意图,理解“使得,两个村庄到此处处理垃圾都比较方便”的含义,灵活运用勾股定理构造方程是答此题的关键.
9.【答案】
【解析】【分析】
此题主要考查了图形变化类,此题在相交线的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊向一般猜想的方法.
根据题意,结合图形,发现:条直线相交最多有个交点,条直线相交最多有个交点,条直线相交最多有个交点,故可猜想,条直线相交,最多有个交点.
【解答】
解:条直线相交最多有个交点,条直线相交最多有个交点,条直线相交最多有个交点,而,,,
七条直线相交最多有交点的个数是:.
故选:.
10.【答案】
【解析】解:,
,
,
,
,
.
故选:.
根据三角板的特点和三角形外角的性质求解即可.
此题考查了两个直角三角板角度的特点,三角形外角的性质,解题的关键是熟练掌握以上知识点.
11.【答案】
【解析】解:,
,
::,,
,
,
.
故答案为:.
根据已知条件求出,再根据对顶角相等求出,再利用即可求出结果.
本题考查了垂线,对顶角的定义和角的和差计算,熟练掌握对顶角的定义是解题的关键.
12.【答案】
【解析】解:根据点到直线垂线段最短,当时,最短.
设,则,
在中,,
,
,
在中,,由勾股定理得,
,即;
解得,
.
故答案为:.
根据点到直线垂线段最短,当时,最短,计算垂线段长即可.
本题考查了垂线段最短,熟练掌握勾股定理计算边长是解答本题的关键.
13.【答案】垂线段最短
【解析】解:,点到的距离是线段的长,故AC,
点到的距离是线段的长,故BC,
所以边最长,依据为垂线段最短,
故答案为:垂线段最短.
结合图形和已知条件,根据点到直线的距离的定义和垂线段最短求解.
本题考查了点到直线的距离的定义以及垂线段最短的性质,解题的关键是熟练掌握相关基础知识.
14.【答案】
【解析】【分析】
此题主要考查了相交线,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊向一般猜想的方法.
根据题意,结合图形可猜想,条直线相交,最多有个交点.
【解答】
解:条直线相交最多有个交点,条直线相交最多有个交点,条直线相交最多有个交点,
而,,,
条直线相交,最多有个交点,
当时,.
故答案为.
15.【答案】上
【解析】解:线段的长是点到直线的距离,
,
,
,重合,
则点在直线上.
,理由如下:
,
与上各点的连线段中,垂线段最短.
.
由线段的长是点到直线的距离,可得,结合,从而可得答案;
由垂线段最短可得答案.
本题考查的是点到直线的距离,垂线段最短,熟记点到直线的距离的含义是解本题的关键.
16.【答案】解:如图,点即为所求;
如图,线段即为所求.
【解析】由点到的距离的长等于的长知点在平分线上,再根据角平分线的尺规作图即可得;
根据过直线外一点作已知直线的垂线的尺规作图即可得.
本题考查作图复杂作图、角平分线的性质定理等知识,解题的关键是熟练掌握基本作图,灵活运用所学知识解决问题,属于中考常考题型.
17.【答案】解:如图,点即为所求;
过点作于点.
由作图可知平分,,,
,
,,,
,
,
,
,
.
【解析】作射线平分交于点,点即为所求;
过点作于点利用面积法求解即可.
本题考查作图复杂作图,角平分线的性质定理,三角形的面积等知识,解题的关键是学会利用面积法解决问题.
18.【答案】【小题】
如图所示沿走最近理由:两点之间线段最短.
【小题】
如图所示沿走最近理由:垂线段最短.
【小题】
如图所示沿走最近理由:垂线段最短.
【解析】 略
略
略
19.【答案】【小题】
或
或
【小题】
或
【解析】 略
略
20.【答案】【小题】
,.,.,.
【小题】
理由如下:,,,即,.
【解析】 见答案
见答案
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
