平方差公式 课件
图片预览


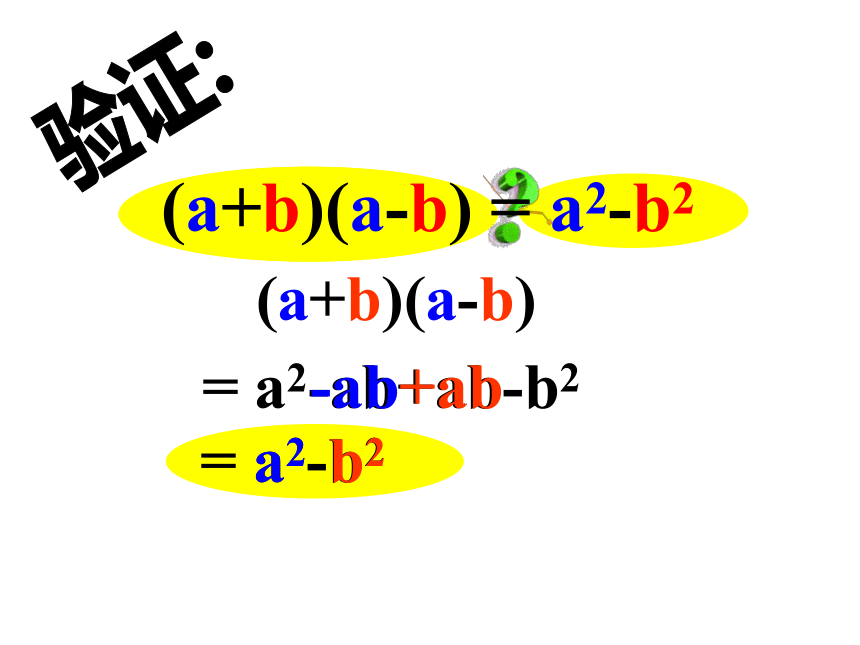



文档简介
课件27张PPT。规律探索:计算下列多项式的积: (x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =x2 - 1m2 - 44x2 - 1你发现了什么?(a+b)(a-b) = a2-b2
验证:(a+b)(a-b)= a2-ab+ab-b2-ab+ab= a2-b2a2b2(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。平方差公式 (a+b)(a-b)=a2-b2
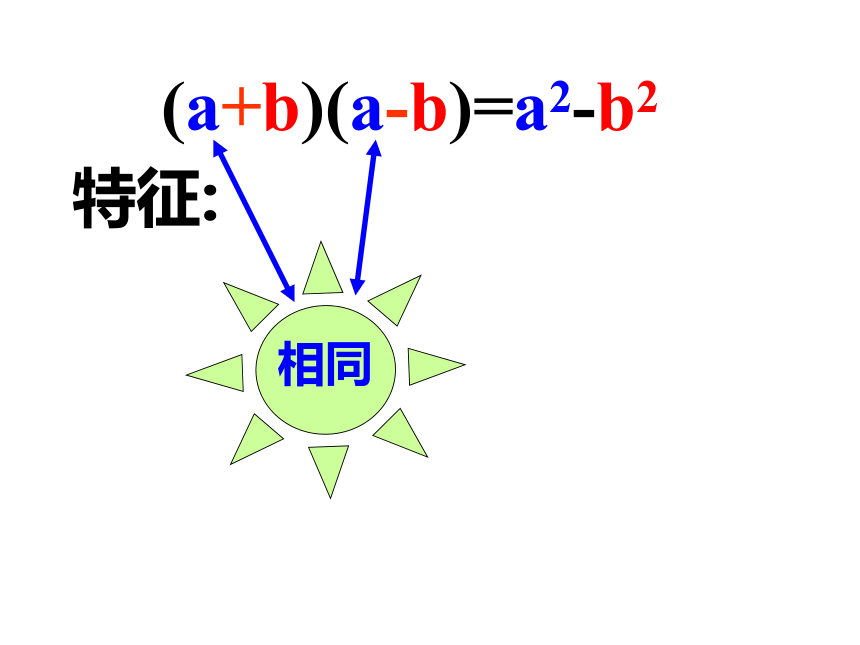
特征:(a+b)(a-b)=a2-b2
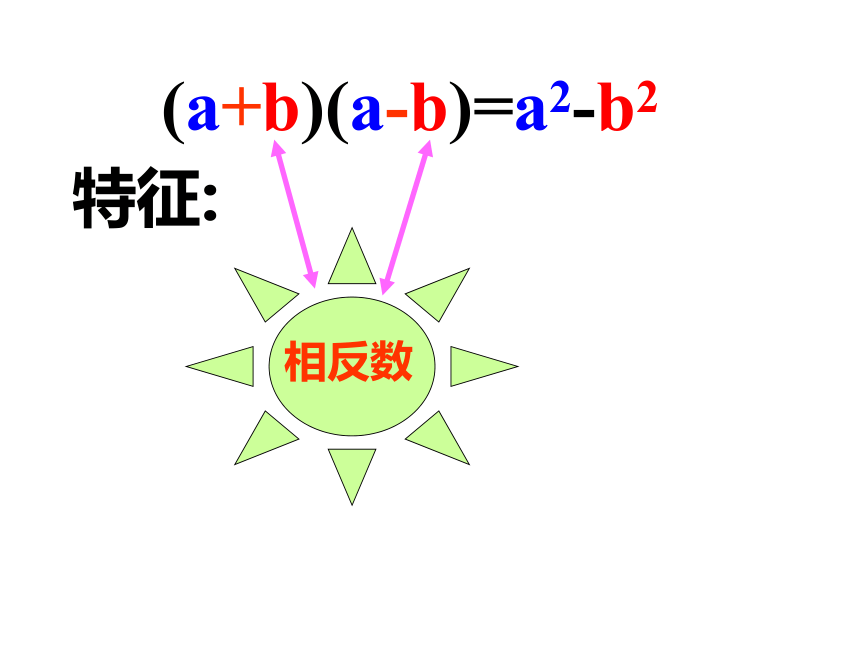
特征:(a+b)(a-b)=a2-b2
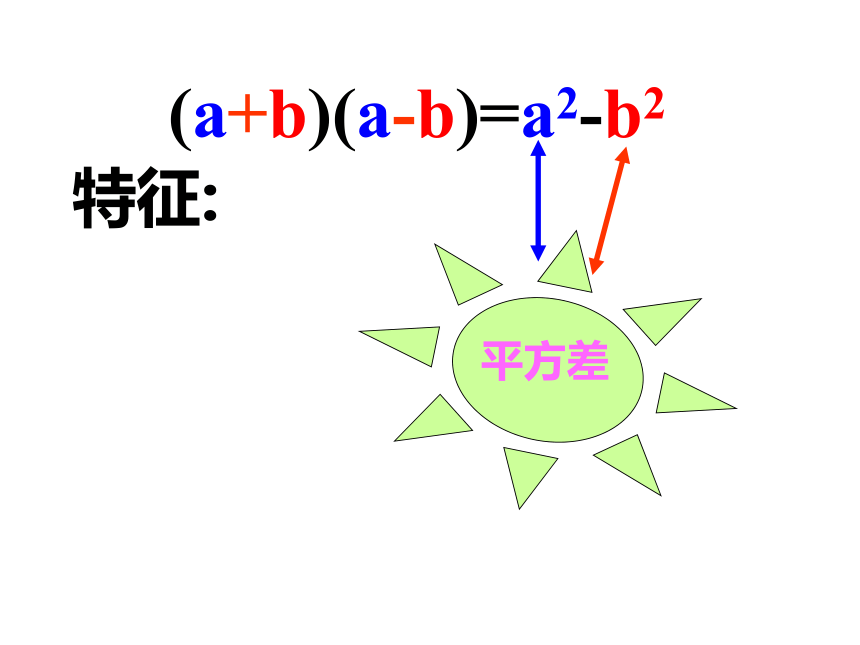
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
平方差公式的特征,在学习时应注意:
(1)左边是两个二项式相乘,并且这两上二项式中有一项完全相同,另一项互为相反数.
(2)右边是乘式中两项的平方差(相同项的平方减去相反项的平方).
(3)公式中的a,b可以表示 一个单项式也可以表示一个多项式.选择下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)AC例1 运用平方差公式计算: ⑴ (3x+2)(3x-2) ;⑵ (b+2a)(2a-b); (3) (-x+2y)(-x-2y).分析: ⑴ (3x+2)(3x-2) 3x3xaa22bb= a2 - b2=(3x)2-22用公式关键是识别两数
完全相同项 — a
互为相反数项— b解: ⑴ (3x+2)(3x-2) =(3x)23x3x-2222= 9x2 - 4⑵ (b+2a)(2a-b);b-b+2a2a=(2a+b)(2a-b)2a2a=(2a)2 =4a2 – b2bb-b2 要认真呀! (3) (-x+2y)(-x-2y) = (-x)2-(2y)2= x2-4y2ㄨ判断 下面各式的计算对不对?
如果不对,应当怎样改正?X2 - 4ㄨ4 - 9a2填空 运用平方差公式计算:a2 - 9b24a2 - 9 练一练注意: 运用公式前,首先要判断两个多项式能否变形为公式的标准形式。我能行!运用平方差公式计算:1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 (a+b+c)(2a-b-c) =m2-n2y2-x24a2-b2x4-y4(a+b)(a-b)=a2-b2
(a+b) 2-c2www.czsx.com.cn小试牛刀⑴ 102 ×98102= (100+2)98(100-2)= 1002-22= 10000-4= 9996⑵ (y+2)(y-2)-(y-1)(y+5)yyyy22= y2 - 2215- (y2+4y-5)= y2-4-y2-4y+5= -4y+1灵活运用平方差公式计算:变式延伸(1)(3x+4)(3x-4) – (2x+3)(3x-2);
(2)(x+y)(x-y)(x2+y2);
挑战极限王二小同学在计算(2+1)(22+1)(24+1)时,
将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1) = (22-1)(22+1)(24+1)= (24-1)(24+1)= 28-1挑战极限 你能根据上题计算:
(2+1)(22+1)(24+1)(28+1) … (2128+1) 的结果吗?
难度提升 你能根据上题再一次计算:
(6+1)(62+1)(64+1)(68+1) … (6128+1) 的结果吗?
二、运用平方差公式的关键:找到公式中的a和b.
技巧:1、判—找出相同项(公式中的a)和相反项(公式中的b);
2、调—化成公式的标准形式;
3、套—利用公式计算。小结一、了解平方差公式的特点:
(1)左边是两个二项式相乘,并且这两上二项式中有一项完全相同,另一项互为相反数.
(2)右边是乘式中相同项的平方减去相反项的平方. www.czsx.com.cn
(m+2)(m-2) =
(2x+1)(2x-1) =x2 - 1m2 - 44x2 - 1你发现了什么?(a+b)(a-b) = a2-b2
验证:(a+b)(a-b)= a2-ab+ab-b2-ab+ab= a2-b2a2b2(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。平方差公式 (a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
平方差公式的特征,在学习时应注意:
(1)左边是两个二项式相乘,并且这两上二项式中有一项完全相同,另一项互为相反数.
(2)右边是乘式中两项的平方差(相同项的平方减去相反项的平方).
(3)公式中的a,b可以表示 一个单项式也可以表示一个多项式.选择下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D.(a-b+c)(b-a-c)
2.下列多项式相乘,不能用平方差公式计算的是( )
A.(x-2y)(2y+x) B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y) D.(-2b-5)(2b-5)AC例1 运用平方差公式计算: ⑴ (3x+2)(3x-2) ;⑵ (b+2a)(2a-b); (3) (-x+2y)(-x-2y).分析: ⑴ (3x+2)(3x-2) 3x3xaa22bb= a2 - b2=(3x)2-22用公式关键是识别两数
完全相同项 — a
互为相反数项— b解: ⑴ (3x+2)(3x-2) =(3x)23x3x-2222= 9x2 - 4⑵ (b+2a)(2a-b);b-b+2a2a=(2a+b)(2a-b)2a2a=(2a)2 =4a2 – b2bb-b2 要认真呀! (3) (-x+2y)(-x-2y) = (-x)2-(2y)2= x2-4y2ㄨ判断 下面各式的计算对不对?
如果不对,应当怎样改正?X2 - 4ㄨ4 - 9a2填空 运用平方差公式计算:a2 - 9b24a2 - 9 练一练注意: 运用公式前,首先要判断两个多项式能否变形为公式的标准形式。我能行!运用平方差公式计算:1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 (a+b+c)(2a-b-c) =m2-n2y2-x24a2-b2x4-y4(a+b)(a-b)=a2-b2
(a+b) 2-c2www.czsx.com.cn小试牛刀⑴ 102 ×98102= (100+2)98(100-2)= 1002-22= 10000-4= 9996⑵ (y+2)(y-2)-(y-1)(y+5)yyyy22= y2 - 2215- (y2+4y-5)= y2-4-y2-4y+5= -4y+1灵活运用平方差公式计算:变式延伸(1)(3x+4)(3x-4) – (2x+3)(3x-2);
(2)(x+y)(x-y)(x2+y2);
挑战极限王二小同学在计算(2+1)(22+1)(24+1)时,
将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1) = (22-1)(22+1)(24+1)= (24-1)(24+1)= 28-1挑战极限 你能根据上题计算:
(2+1)(22+1)(24+1)(28+1) … (2128+1) 的结果吗?
难度提升 你能根据上题再一次计算:
(6+1)(62+1)(64+1)(68+1) … (6128+1) 的结果吗?
二、运用平方差公式的关键:找到公式中的a和b.
技巧:1、判—找出相同项(公式中的a)和相反项(公式中的b);
2、调—化成公式的标准形式;
3、套—利用公式计算。小结一、了解平方差公式的特点:
(1)左边是两个二项式相乘,并且这两上二项式中有一项完全相同,另一项互为相反数.
(2)右边是乘式中相同项的平方减去相反项的平方. www.czsx.com.cn
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
