数学九年级上青岛版1.2怎样判定三角形相似课件13
文档属性
| 名称 | 数学九年级上青岛版1.2怎样判定三角形相似课件13 |  | |
| 格式 | zip | ||
| 文件大小 | 726.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 06:56:30 | ||
图片预览






文档简介
课件17张PPT。怎样判定三角形相似课前回顾 类似于判定三角形全等的SSS方法,我们能不能通过三边间的关系来判定两个三角形相似呢?定义法、方法1(两角型)、方法2(两边夹角型)2.到目前,你学了几种判定两三角形相似的
方法呢? 能!1.什么叫相似三角形?学习目标:1、经历探索三角形相似的判定方法(3)的过程,进一步体
会数学学习的基本方法。
2、能利用判定方法3判定两三角形是否相似;会利用三角形的
相似解决一些简单的实际问题。
3、在探索过程及解决问题的过程中,发展学生的合情推理能
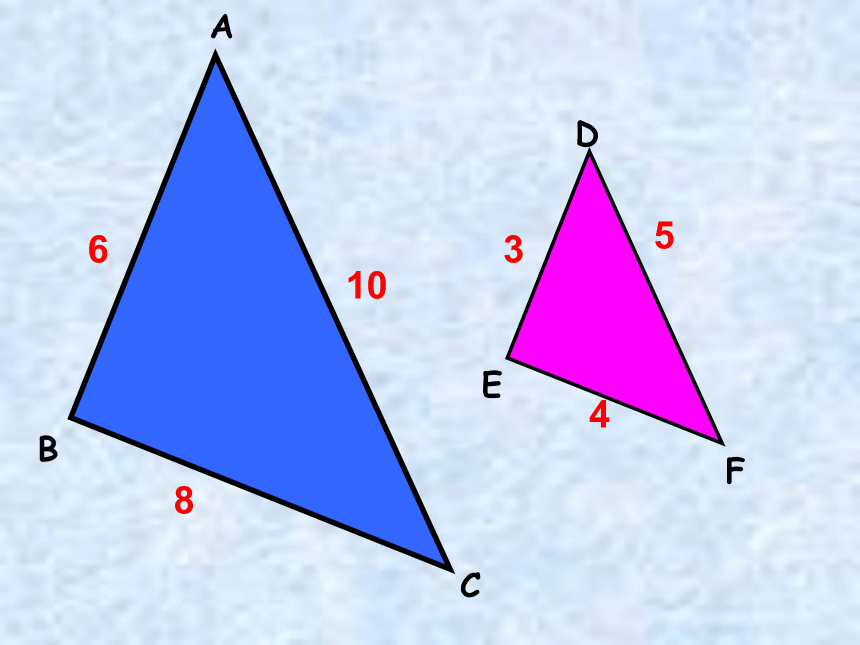
力。实验与探究拿出你课前制作的△ABC和△DEF,(小组内相互交流完成下面几个问题)
(1)分别计算 , , ,这三个比值相等吗?
(2)利用叠合的方法,检验对应内角之间具有怎样的大小关系。
(3)△ABC和△DEF相似吗?为什么?(4)由此你猜想得到什么结论?(5)适当改变△ABC和△DEF的边长,并保持
= = ,还能得到同样的结论吗?ACBEFD8610345 判定方法三:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。 简单的说:三边对应成比例的两三角形相似。几何语言:∵∴△A′B′C′∽△ABC结论火眼金睛你能找出下图中的相似三角形吗?4cm3cm2cm12cm16cm8cm6cm3cm5cm(1)(2)(3)注意:对应边的找法——长对长,短对短,中对中。如图,已知 ,找出图中
相等的角,并说明你的理由。解:在ΔABC和ΔADE 中,
∵
∴ ΔABC∽ΔADE
∴ ∠BAC=∠DAE, ∠B= ∠D,
∠C= ∠E
你能行12 如图,某地四个乡镇A,B,C,D之间建有公路,已知AB=14千米,AD=28千米,BD=21千米, BC=42千米,DC=31.5千米,公路AB与CD平行吗? 说出你的理由。1428214231.5解:公路AB与CD平行。
∵
∴
∴ △ABD∽△BDC,
∴ ∠ABD=∠BDC
∴ AB∥DC 小试身手211428BAD通过对本节课的学习,你有哪些收获呢?你还有什么疑惑吗?大家谈收获挑战自我 方格纸中,每个小格的顶点叫做格点,以格点之间的连线为边的三角形叫做格点三角形,如图,△ ABC 和△DEC是两个格点三角形。
(1) △ABC与△DEC相似吗?为什么?
(2)在图中右侧的网格中画一个格点三角形MNP,使△MNP ∽ △ABC,并且对应边的比等于 。ACBDEM325 练一练: 已知△ABC和 △DEF,根据下列
条件判断它们是否相似.(3) AB=12, BC=15, AC=24
DE=16, EF=20, DF=30(2) AB=4, BC=8, AC=10
DE=20, EF=16, DF=8(1) AB=3, BC=4, AC=6
DE=6, EF=8, DF=9是否否(温馨提示:长对长,短对短,中对中)当堂检测如图,AB=12,AC=6,AD= 8,
BC=16,CD=3.问⊿ ACD与
⊿ ABC相似吗?请说明你的理由.
1263168ABCD练一练试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE 要做两个形状相同的三角形框架,其中一个三角形框架的三边的长分别为4、5、6,另一个三角形框架的一边长为2,请你想一想应该怎样选择材料可使这两个三角形相似?你有几种选材方案?解:设另一个三角形的另两边的长分别为x、y。因为这两个三角形相似,所以拓展提升再见谢谢同学们的合作!
方法呢? 能!1.什么叫相似三角形?学习目标:1、经历探索三角形相似的判定方法(3)的过程,进一步体
会数学学习的基本方法。
2、能利用判定方法3判定两三角形是否相似;会利用三角形的
相似解决一些简单的实际问题。
3、在探索过程及解决问题的过程中,发展学生的合情推理能
力。实验与探究拿出你课前制作的△ABC和△DEF,(小组内相互交流完成下面几个问题)
(1)分别计算 , , ,这三个比值相等吗?
(2)利用叠合的方法,检验对应内角之间具有怎样的大小关系。
(3)△ABC和△DEF相似吗?为什么?(4)由此你猜想得到什么结论?(5)适当改变△ABC和△DEF的边长,并保持
= = ,还能得到同样的结论吗?ACBEFD8610345 判定方法三:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。 简单的说:三边对应成比例的两三角形相似。几何语言:∵∴△A′B′C′∽△ABC结论火眼金睛你能找出下图中的相似三角形吗?4cm3cm2cm12cm16cm8cm6cm3cm5cm(1)(2)(3)注意:对应边的找法——长对长,短对短,中对中。如图,已知 ,找出图中
相等的角,并说明你的理由。解:在ΔABC和ΔADE 中,
∵
∴ ΔABC∽ΔADE
∴ ∠BAC=∠DAE, ∠B= ∠D,
∠C= ∠E
你能行12 如图,某地四个乡镇A,B,C,D之间建有公路,已知AB=14千米,AD=28千米,BD=21千米, BC=42千米,DC=31.5千米,公路AB与CD平行吗? 说出你的理由。1428214231.5解:公路AB与CD平行。
∵
∴
∴ △ABD∽△BDC,
∴ ∠ABD=∠BDC
∴ AB∥DC 小试身手211428BAD通过对本节课的学习,你有哪些收获呢?你还有什么疑惑吗?大家谈收获挑战自我 方格纸中,每个小格的顶点叫做格点,以格点之间的连线为边的三角形叫做格点三角形,如图,△ ABC 和△DEC是两个格点三角形。
(1) △ABC与△DEC相似吗?为什么?
(2)在图中右侧的网格中画一个格点三角形MNP,使△MNP ∽ △ABC,并且对应边的比等于 。ACBDEM325 练一练: 已知△ABC和 △DEF,根据下列
条件判断它们是否相似.(3) AB=12, BC=15, AC=24
DE=16, EF=20, DF=30(2) AB=4, BC=8, AC=10
DE=20, EF=16, DF=8(1) AB=3, BC=4, AC=6
DE=6, EF=8, DF=9是否否(温馨提示:长对长,短对短,中对中)当堂检测如图,AB=12,AC=6,AD= 8,
BC=16,CD=3.问⊿ ACD与
⊿ ABC相似吗?请说明你的理由.
1263168ABCD练一练试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE 要做两个形状相同的三角形框架,其中一个三角形框架的三边的长分别为4、5、6,另一个三角形框架的一边长为2,请你想一想应该怎样选择材料可使这两个三角形相似?你有几种选材方案?解:设另一个三角形的另两边的长分别为x、y。因为这两个三角形相似,所以拓展提升再见谢谢同学们的合作!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
