数学九年级上青岛版1.4图形的位似课件8
文档属性
| 名称 | 数学九年级上青岛版1.4图形的位似课件8 |

|
|
| 格式 | zip | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 06:58:15 | ||
图片预览






文档简介
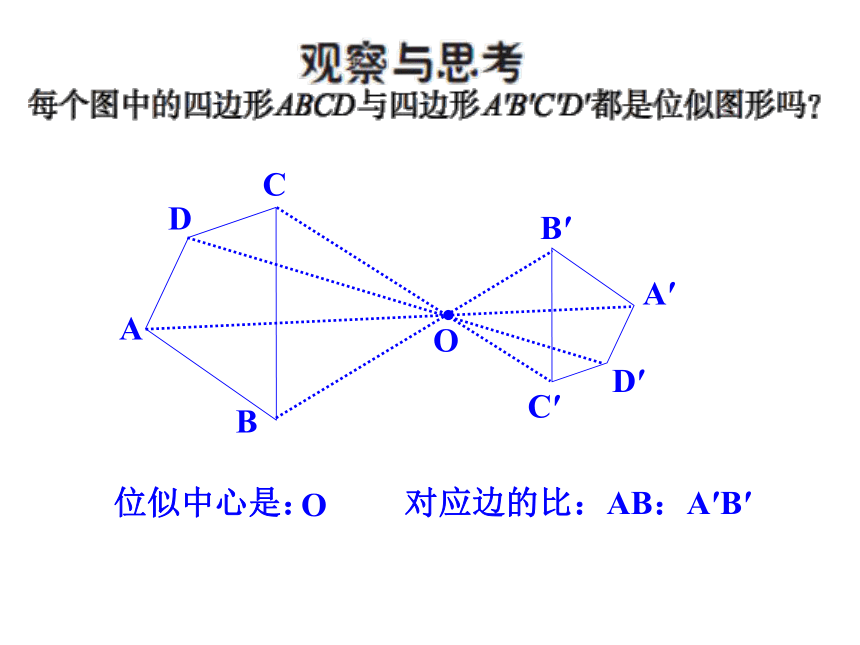
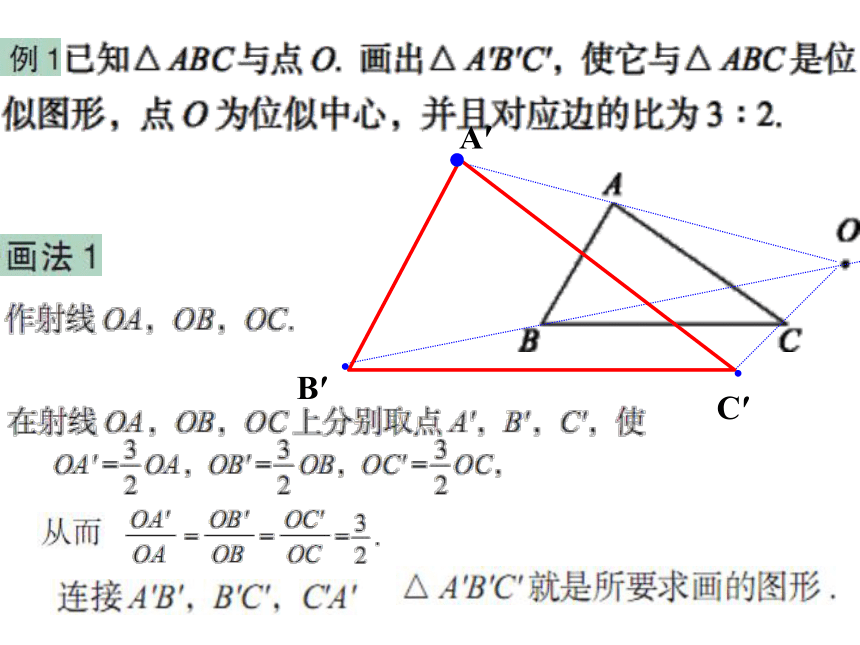
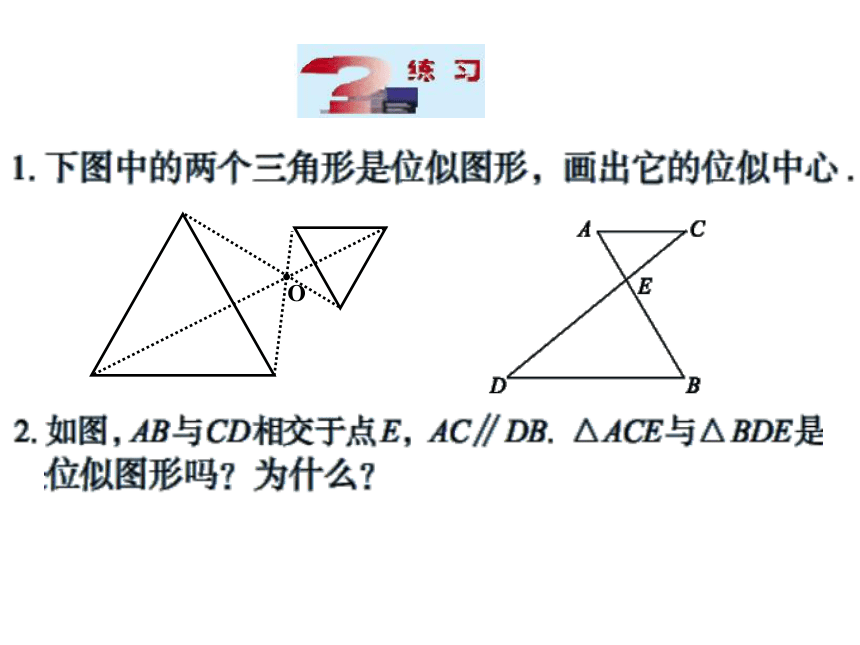
课件27张PPT。§1.4图形的位似认真阅读课本第64、65页,回答以下问题:1、什么叫相似图形?2、什么叫位似图形?位似中心?位似比?3、位似图形有什么性质?4、如何作位似图形?位似图形每对对应点所在直线都交于一点的相似图形,叫做位似图形ABCA′B′C′O△ABC和△A′B′C′是一对位似图形,点O叫做位似中心,对应边的比为2:1ABCDA′B′C′D′O 位似中心是:O对应边的比:AB:A′B′位似中心是:点OO对应边的比:AB:A′B′A B C D A′ B′ C′ D′ A B C D (A′) B′ C′ D′ 位似中心是:点A 如果两个多边形是位似图形,且对应边平行或在同一直线上,那么图形上任意一对对应点到位似中心的距离之比都等于对应边的比。A′B′C′A′B′C′通过上例,我们知道:利用位似,我们可以将一个图形放大或缩小。O B'A'xyBAo在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.A′(2,1),B′(2,0)观察对应点之间的坐标的变化,你有什么发现?探索1:B'A'xyBAo在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.A′(2,1),B′(2,0)A〞B〞A〞(-2,-1),B(-2,0)在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.观察对应点之间的坐标的变化,你有什么发现?xyo在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2画它的位似图形.BACA′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )放大后对应点的坐标分别是多少?B'A'C'探索2:还有其他办法吗?A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )xyo在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )BAC放大后对应点的坐标分别是多少?xyo例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )A′B′C′D′你还有其他办法吗?试试看.xyoB1.如图表示△ABC把它缩小后得到的△COD,求它们的相似比ACD练一练:xyo2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.BAC练一练:xyo3.如图,写出矩形wxyz各点的坐标,如果矩形STUV相似于wxyz,点S 的坐标为(2,2),按照下列相似比,分别写出T、U、V各点的坐标. W x y z(1)相似比为2;(2)相似比为 ;练一练: 如果两个图形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形, 这个点叫做位似中心, 这时的相似比又称为位似比.1.什么叫位似图形?2.位似图形的性质 位似图形上的任意一对对应点到位似中心的距离之比等于位似比3.利用位似可以把一个图形放大或缩小复习回顾DEFAOBC如何把三角形ABC放大为原来的2倍?DEFAOBC对应点连线都交于____________对应线段_______________________________位似中心平行或在一条直线上复习回顾B'A'xyBAo在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.A′(2,1),B′(2,0)观察对应点之间的坐标的变化,你有什么发现?探索1:B'A'xyBAo在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.A′(2,1),B′(2,0)A〞B〞A〞(-2,-1),B(-2,0)在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.观察对应点之间的坐标的变化,你有什么发现?xyo在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2画它的位似图形.BACA′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )放大后对应点的坐标分别是多少?B'A'C'探索2:还有其他办法吗?A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )xyo在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )BAC放大后对应点的坐标分别是多少?xyo例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )A′B′C′D′你还有其他办法吗?试试看.xyoB1.如图表示△ABC把它缩小后得到的△COD,求它们的相似比ACD练一练:xyo2.如图△ABC的三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.BAC练一练:xyo3.如图,写出矩形wxyz各点的坐标,如果矩形STUV相似于wxyz,点S 的坐标为(2,2),按照下列相似比,分别写出T、U、V各点的坐标. W x y z(1)相似比为2;(2)相似比为 ;练一练:
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
