数学九年级上青岛版1.4图形的位似课件9

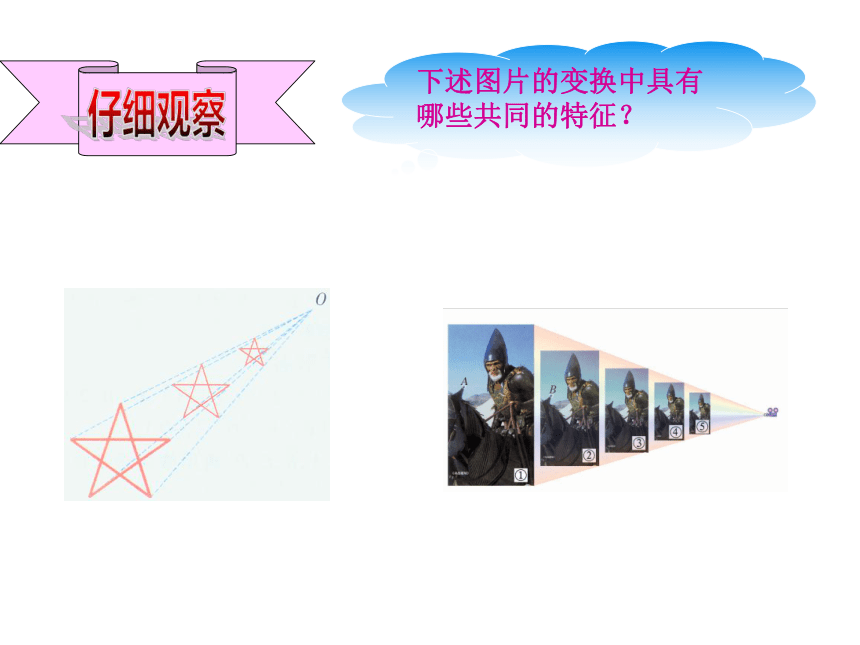
课件41张PPT。图形的位似下述图片的变换中具有哪些共同的特征？
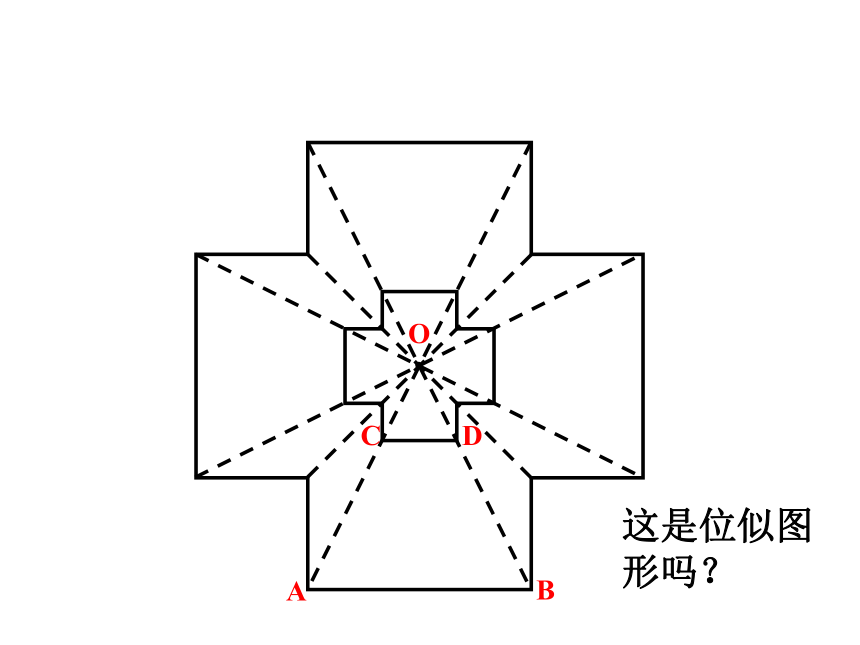
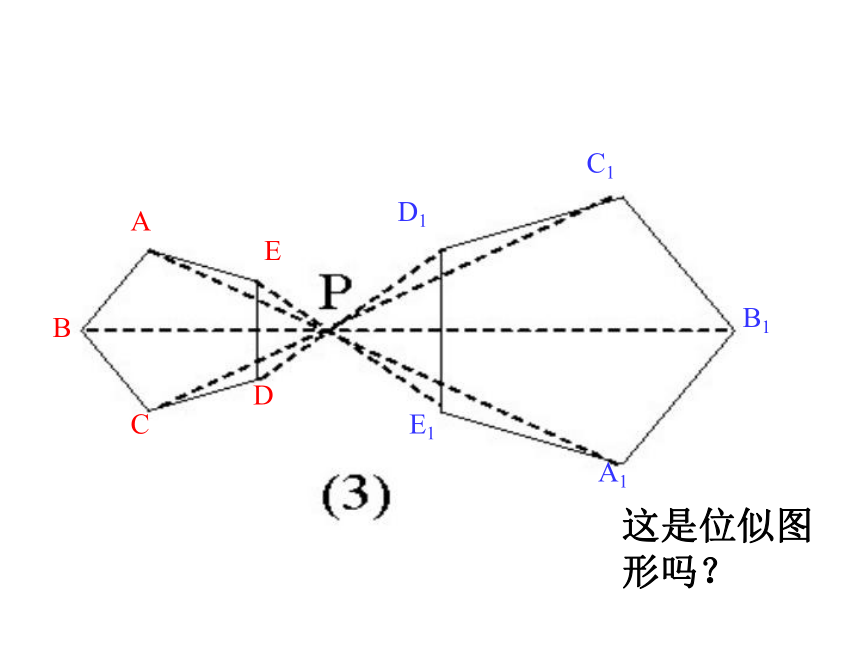
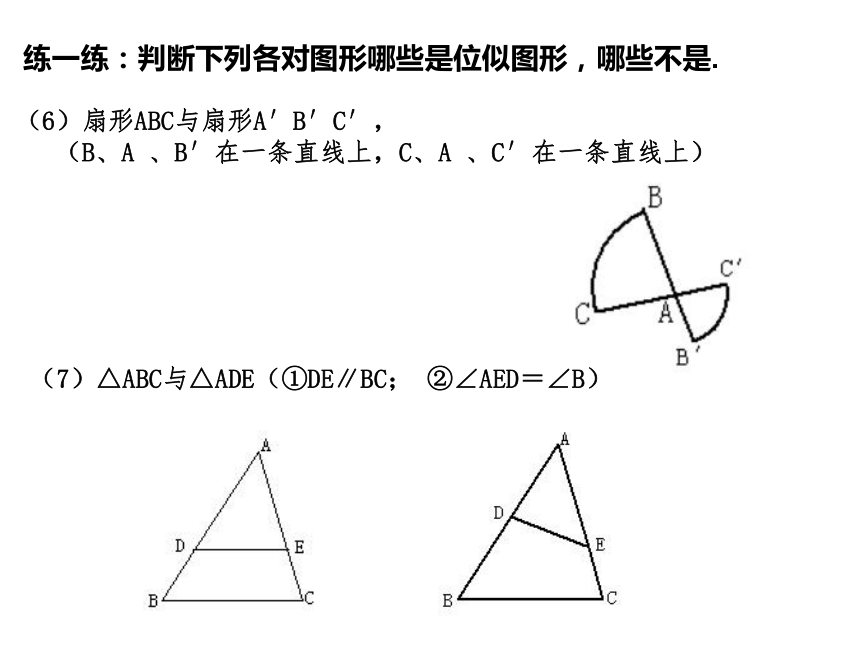
下面的一组图片是形状相同的图形,在图片①上取一点A,它与另一图片(如图片②)上的相应点B之间的连线是否经过镜头P的中心?在图片上换其它的点试一试,还有类似的结论吗?①PA②③④⑤BCDEF如果两个图形对应点所在的直线交于同一点,并且对应点到这点的距离成比例，那么这两个图形叫做位似图形, 这个点叫做位似中心.这个交点叫做位似中心, 这时两个相似图形的相似比又叫做它们的位似比.这是位似图形吗？显然，位似图形是相似图形的特殊情形. 这是位似图形吗？这是位似图形吗？练一练1：判断下列各对图形哪些是位似图形，哪些不是. （1）五边形ABCDE与五边形A′B′C′D′E′； （2）在平行四边形ABCD中，△ABO与△CDO 练一练：判断下列各对图形哪些是位似图形，哪些不是. （3）正方形ABCD与正方形A′B′C′D′. （4）等边三角形ABC与等边三角形A′B′C′练一练：判断下列各对图形哪些是位似图形，哪些不是. 练一练：判断下列各对图形哪些是位似图形，哪些不是. （6）扇形ABC与扇形A′B′C′，
（B、A 、B′在一条直线上，C、A 、C′在一条直线上） （7）△ABC与△ADE（①DE∥BC； ②∠AED＝∠B） 2．如图P，E，F分别是AC，AB，AD的中点，四边形AEPF与四边形ABCD是位似图形吗？如果是位似图形，说出位似中心和位似比. 位似图形的性质 一般地，位似图形有以下性质：
1. 位似图形是相似图形
2.位似图形的每组对应点所在的直线都交于一点；
3.位似图形上任意一对对应点到位似中心的距离之比等于位似比.
4. 位似图形对应线段所在直线平行或共线.认一认：它们是位似图形吗？4364.525练　一　练下列说法正确的是（???? ）　　
A.两个图形如果是位似图形，那么这　　　　　　　两个图形一定全等；B.两个图形如果是位似图形，那么这　　　　两个图形不一定相似；? C.两个图形如果是相似图形，那么这两个图形一定位似；D.两个图形如果是位似图形，那么这两个图形一定相似。 在下列每个图形中，位似图形的对应线段AB与A′B′是否平行？BC与B′C′，CD与C′D′，AD与A′D′是否平行？位似图形中不经过位似中心的对应线段平行.位似图形上任意一对对应点到位似中心的距离之比等于位似比。分清谁比谁!位似图形上任意一对对应点到位似中心的距离之比等于位似比。分清谁比谁!下列图形中，每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图，你发现每个图中的两个四边形各对应点的连线交点的位置在何处？1. 位似变换是相似变换的特例，位似图形一定是相似图形，但相似图形不一定是位似图形.
2.位似中心可以在两个图形的同侧,或在两个图形之间,或在图形内,或在边上或顶点上.
3.位似中心在连接两个对应点的线段之外称为外位似;
位似中心在连接两个对应点的线段之上称为内位似.做　一　做：按如下方法可以将△ABC的三边缩小为原来的1/2:O如图,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F; △DEF的三边就是△ABC相应三边的1/2. 实际上△ABC与△DEF是位似图形.如果在射线OA,OB,OC上分别取D,E,F,使OD=2OA, OE=2OB, OF=2OC,那么,结果又会怎样?结果会得到一个放大了的△DEF,且△DEF的三边是△ABC三边的2倍.即它们的位似比是2∶1.已知三角形ABC，在三角形ABC外任取一点O，如果在射线AO,BO,CO上分别取点D,E,F使DO=2OA,EO=2OB,FO=2OC,那么,结果会怎样呢?画出图形。如图所示,作出一个新图形，使新图形与原图形对应线段的比是2∶1.1.在原图上取几个关键点A,B,C,D,E,F,G;图外任取一点P;2.作射线AP,BP,CP,DP,EP,FP,GP;在这些射线上依次取点A′,B′,C′,D′,E′,F′,G′,使PA′=2PA,PB′=2PB,PC′=2PC,PD′=2PD,PC′=2PC,
PE′ =2PE,PF′=2PF,PG′=2PG;3.顺次连接点A′, B′, C′, D′, E′, F′,G′,所得到的图形(向下的箭头)就是符合要求的图形;实际上,新图形与原图形是位似图形,位似比是2∶1.如果在上面的例题,你还有其它方法吗?
如果依次在射线上PA,PB,PC,PD,PE,PF,PG上取点A′,B′,C′,D′,E′,F′,G′呢?结果是一个向上的箭头.
新图形与原图形是位似图形,位似比是2∶1利用位似将图形放大或缩小的作图步骤：
第一步：在原图上选取关键点若干个,并在原图外任取一点P.
第二步：以点P为端点向各关键点作射线（或以关键点为端点向点P作射线）.
第三步：分别在射线上取关键点的对应点，满足放缩比例.
第四步：顺次连接截取点.
即可得到符合要求的新图形.
简记方法:（1）选点；（2）作射线；
（3）定对应点；（4）连线. A″B″···（3，0）（0，2）（3，2）C″作位似图形 例： 如图，请以坐标原点O为位似中心，作四边形ABCD的位似图形，位似比为 .
能画出几个？62页例题如图,平面直角坐标系,A(6,3),B(6,0),以原点O为位似中心,相似比为1/3将AB进行变换,画出变换后的图形,并求出相应的坐标.如图,A(2,3),B(1,1),C(5,2)以原点O为位似中心,相似比为2, 将△ABC进行变换,画出变换后的图形,并求出相应的坐标.直角坐标系中图形的位似变化与对应点坐标变化的规律 以坐标原点为位似中心的位似变换有一下性质：
若原图形上点的坐标为（x，y），像与原图形的位似比为k，则像上的对应点的坐标为（kx，ky）或（―kx，―ky）. 归纳:
在平面直角坐标系中,如果位似变换是以原点的位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或 – k.
说明:
1. 在原点同侧,坐标比为k,异侧坐标比为 –k;
2.有时画出一种即可.
3.以原点为位似中心的两个新图形关于原点中心对称.4.平移、旋转与轴对称变换、位似变换都是几何变换。四种变换中，平移、旋转与轴对称都是全等变换，变换前后的图形是全等的，而位似变换前后得到的图形不全等，它们是相似的。
5.四种变换的坐标表示：以点P(a,b)为例.
（1）将点P向右平移m个单位得P/(a+m,b)；将点P向下平移m个单位得P/(a,b- m).
（2）点P关于x轴的对称点P/(a,-b)；点P关于y轴的对称点P/(-a, b).
（3）将点P绕坐标原点旋转180o后，得到点P/(-a,-b)，也叫P与P/关于原点中心对称.
（4）将点P与原点的距离扩大到m倍，得到点P/(ma,mb)或(-ma,-mb) 2. 位似图形的每组对应点所在的直线都交于一点.3.位似图形的对应点和位似中心在同一条直线上,它们到位似中心的距离之比等于相似比.4.位似图形中不经过位似中心的对应线段平行.1. 位似图形是相似图形.小结