数学九年级上青岛版2.1锐角三角比课件

课件18张PPT。第2章 解直角三角形2.1 锐角三角比教材分析：《锐角三角比》是青岛版八年级数学下册第九章的内容，属于三角学，是《数学课程标准》中“空间与图形”领域的重要内容。它是在学生已学习了“相似三角形”、“勾股定理”等内容基础上,这为过渡到本节的学习起着铺垫作用。从《数学课程标准》看，中学数学把三角学内容分成两个部分，第一部分放在义务教育第三学段，第二部分放在高中阶段。在义务教育第三学段，主要研究锐角三角比和解直角三角形的内容，无论是从内容上看，还是从思考问题的方法上看，这一部分都是后部分的重要基础，也为后面学习特殊角的三角比做好准备，同时也是后面学习解直角三角形的基础；在高中，它是进一步学习三角函数的基础，也是研究直角三角形边角关系的重要工具而直角三角形中边角间的关系是应用广泛的数学知识之一。因此本节课的地位非常重要，起着承上启下的作用。
知识技能：
（1）通过实验、观察、探究、交流、猜测等数学活动，探索锐角三角比的意义。
（2）理解锐角三角比的概念，记住三角比的符号，会进行锐角三角比的文字语言和符号语言的转化。
数学思考：
经历当直角三角形的锐角固定时，它的对边与斜边的比值是固定值，发展学生的形象思维，培养学生由特殊到一般的演绎推理能力。并由此得到它的邻边与斜边的比值、它的对边与它的邻边的比值也是固定值。
解决问题：
从实际问题入手研究，经历从发现到解决直角三角形中的一个锐角所对对边与斜边之间的关系的过程，体会研究数学问题的一般方法以及所采用的思考问题的方法。
情感态度：
在解决问题的过程中体验求索的科学精神以及严谨的科学态度，进一步激发学习需求。介绍虎丘塔的历史及现状，激发学生的爱国主义热情及学习本章的兴趣，激发学生为祖国骄傲，为祖国学习，为祖国做贡献的决心。【学习目标】
重点：锐角三角比的定义。

难点：已知直角三角形的两边会求一个锐角的三角比。重点与难点：教学设计 【课前延伸】 【课内探究】 【课后提升】 创设情境，引入新课
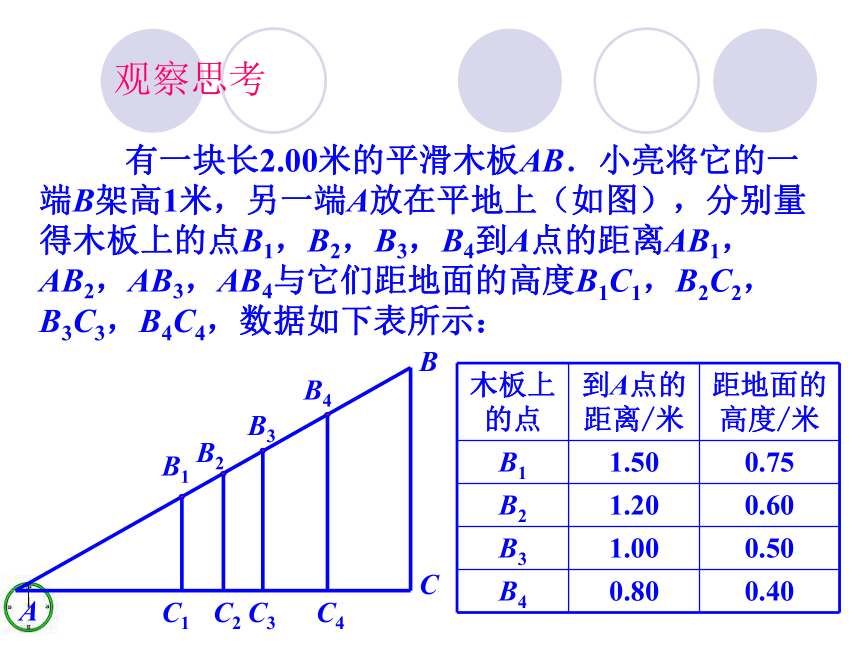
自主学习，发现新知合作学习，探究新知实践应用，精讲点拨学以致用，巩固提高厚积薄发，规律总结板书设计 问题 为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水管，在山坡上修建一座扬水站，对坡面的绿地进行喷灌．现测得斜坡与水平面所成角的度数是30°，为使出水口的高度为30m，那么需要准备多长的水管？这个问题可以归结为，在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝30m，求AB 分析：生活中的数学 有一块长2.00米的平滑木板AB．小亮将它的一端B架高1米，另一端A放在平地上（如图），分别量得木板上的点B1，B2，B3，B4到A点的距离AB1，AB2，AB3，AB4与它们距地面的高度B1C1，B2C2，B3C3，B4C4，数据如下表所示：观察思考自主学习因为Rt△ABC∽ Rt△AB′C′合作探究（观察与思考）（1）如图，作一个锐角A，在∠A的一边上任意取两个点B，B′,经过这两个点分别向∠A的另一边作垂线，垂足分别为C，C′，比值　 与　　相等吗？为什么？AB''CB2）如果设 =k，那么对于确定的锐角A来说，比值k的大小与点B′在AB边上的位置有关吗对于确定的锐角A来说，比值k与点B′在AB边上的位置无关．'B 对于确定的锐角A来说，比值k与点B′在AB边上的位置无关，只与锐角A的大小有关．？记作sinA，即记作cosA，即记作tanA，即锐角A的正弦、余弦、正切统称锐角A的三角比．演示一个锐角A的三角比只与它的大小有关．注：1．sinA,cosA,tanA分别是一个完整的记号．记号里习惯省去角的符号“∠”，不能理解成 sin·A,cos·A,tan·A． 2．通常,把∠A的对边记作a， ∠B的对边记作b， ∠C的对边记作c． 如图，你能用a、b、c表示∠A和∠B的正弦、余弦和正切吗？cab例题讲解（精讲点拨）例１如图，在Rt△ABC中，∠C=90°，AC=4，BC=2，
求∠A的正弦、余弦、正切的值．解：在Rt△ABC中，∠C=90°．
因为AC=4，BC=2，所以421．在Rt△ABC中,各边的长度都扩大两倍,则锐角A的四个三角函数值（ ）

(A)都扩大两倍 (B)都缩小两倍 (C)不变 (D)不能确定3. 如图甲，△ABC中，AC＝3，BC＝4，AB＝5，则tanB＝
4. 如图甲，△ABC中，∠C＝90o，BC＝4，sinA＝，求AC的长。2.如图甲，Rt△ABC中，∠C＝90°，AB＝6，AC＝2，则sinA＝（ ）
（A） 1/3 （B）2/3 （C） （D） ．1． ∠ A的正弦：∠A的余弦：∠A的正切：锐角A的正弦、余弦、正切统称锐角A的三角比．2．一个锐角的三角比只与它的大小有关．厚积薄发（规律总结）板书设计1、锐角三角比
2、一个锐角的三角比与三角形的大小无关，只与角的大小有关 。优胜小组评选
G1:
G2:
G3:
G4:
G5:
G6:
G7:
G8:
拓展延伸（能力从这里提升）如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，如果AC=3厘米，BC=4厘米，设∠ACD=α，求tanα、sinα、cosα的值。同学们,
再见!