数学九年级下青岛版5.5确定二次函数的表达式课件1
文档属性
| 名称 | 数学九年级下青岛版5.5确定二次函数的表达式课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 06:59:47 | ||
图片预览








文档简介
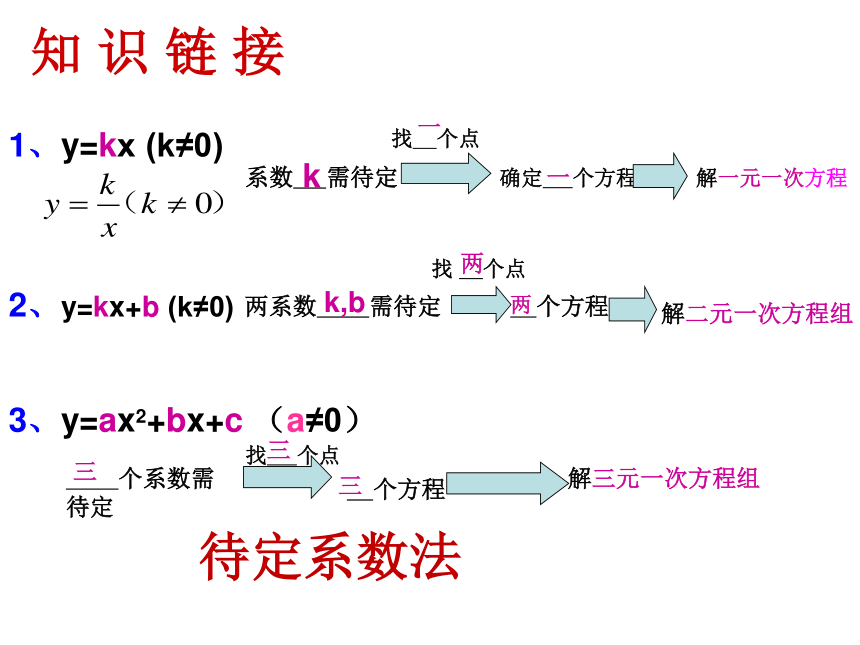
课件26张PPT。确定二次函数的表达式1、y=kx (k≠0)2、y=kx+b (k≠0)系数 需待定找 个点确定 个方程解一元一次方程 两系数 需待定找 个点 个方程解二元一次方程组3、y=ax2+bx+c (a≠0)解三元一次方程组 待定系数法知 识 链 接k一一两三三三k,b两学习目标
1、会用待定系数法确定二次函数表达式.
2、能根据抛物线上两个或三个点的坐标,确定含两个或三个未知系数的二次函数的表达式。例1(1)二次函数y=ax2+bx+c (a≠0)的图象与y轴的交点坐标
是 ;已知二次函数y=x2+2x+c 的图象过(0,-3),则
c= ,所以表达式为 。
探究新知 (3)已知二次函数的图象过点(0,-3) (1, 0)和
(-1,- 4),求这个二次函数的表达式。
(0,c)-3y= x2 + 2x-3(2)已知二次函数y=ax2+c 的图象过点(2, 3)和(0,-5),
求这个二次函数的表达式。
3=4a+c
-5=c
解: 把点(2,3),(0,-5)代入y=ax2+c得,∴二次函数的表达式为:y=2x2-5
c=-5
解之得: a=2
(3)已知二次函数的图象过点(0,-3) (1, 0)和
(-1,- 4),求这个二次函数的表达式。
学以致用 已知二次函数的图象与y轴交点的纵坐标为1,
且经过点(2,5)和(-2,13),求这个二次函数
的表达式。 解: ∵二次函数图象与y轴交点的纵坐标为1,
∴设 y=ax2+bx+1 (a≠0)
又∵图象过(2,5),(-2,13)5=4a+2b+1
13=4a-2b+1a=2
b=-2
解之得:∴y=2x2 - 2x+1∴想一想1、在什么情况下,已知二次函数图象上一点的坐标就可以确定它的表达式?
2、在什么情况下,已知二次函数图象上两点的坐标就可以确定它的表达式?
例2:解:已知抛物线的顶点为(-1,-3),且抛物线过
(-2,-5),求该抛物线的表达式?∴设二次函数表达式为:
y=a(x+1)2-3∵抛物线的顶点为(-1,-3)又点( -2,-5 )在抛物线上∴-5=a-3, 解得a= -2∴所求的抛物线表达式为 y=-2(x+1)2-3
即:y=-2x2-4x-5
已知顶点坐标,如何设二次函数的表达式?
1)顶点(1,-2) 设y= a(x )2
2) 顶点(-1,2) 设y= a(x )2
3)顶点(-1,-2) 设y= a(x )2
4)顶点 (h, k) 设y= a(x )2 -1-2+1+2+1-2- h+ k学以致用 已知二次函数的图象顶点是(-1,1),且经过点(1,-3),求这个二次函数的表达式.解:∵抛物线的顶点为(-1,1)∴设二次函数表达式为:
y=a(x+1)2+1又点( 1,-3 )在抛物线上∴4a+1=-3, 解得a=-1∴所求的抛物线表达式为 y= - (x+1)2+1
即,y= -x2-2x 1、 确定二次函数的表达式的一般步骤:知识盘点一设、二列、三解、四还原.2、确定二次函数表达式常用方法:(1)已知图象上三点或三点的对应值,通常选择一般式.
(2)已知图像的顶点坐标或对称轴和最值,通常选择顶点式. 选择最优解法,求下列二次函数表达式:
1.(必做)已知抛物线的图象经过点(1,1)、(-1,-1)、(0,-2),设抛物线解析式为_______ ___.
2.(必做) 已知抛物线的顶点坐标(-2,3) ,且经过点(-1,0) ,设抛物线解析式为_________ ___.
3.(选做)已知二次函数有最大值6,且经过点(2, 3),(-4,5),设抛物线解析式为___ __ ____.
4.(选做)已知抛物线的对称轴是直线x=-2,且经过点(1,3),(5,6),设抛物线解析式为_____ ___.达标测试y=ax2+bx+c(a≠0)y=a(x+2)2+3(a≠0)y=a(x-h)2+6(a≠0)y=a(x+2)2+k(a≠0)作业布置必做题:习题2.6的1、2题;
选做题:习题2.6的3题。-x1- x2求出下表中抛物线与x轴的交点坐标,看看你有什么发现?(1,0)(3,0)(2,0)(-1,0)(-4,0)(-6,0)(x1,0),( x2,0)y=a(x___)(x____)
(a≠0)探究二次函数解析式-x1- x2求出下表中抛物线与x轴的交点坐标,看看你有什么发现?(1,0)(3,0)(2,0)(-1,0)(-4,0)(-6,0)(x1,0),( x2,0)y=a(x___)(x____)
(a≠0)交点式探究二次函数解析式y=a(x-1)(x-3)(a≠0)y=a(x-2)(x+1)(a≠0)y=a(x+4)(x+6)(a≠0)已知三个点坐标,选择一般式已知顶点坐标或对称轴或最值,选择顶点式 已知抛物线与x轴的两交点坐标,选择交点式二次函数常用的三种解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。 例题?已知二次函数图象经过点(1,4),(-1,0)和(3,0)三点,求二次函数的解析式.解法1:(一般式)
设二次函数解析式为y=ax2+bx+c
∵二次函数图象过点(1,4),(-1,0)和(3,0)
∴? a+b+c=4?????? ①
??? a-b+c=0?????? ②
?? 9a+3b+c=0??? ? ③
①-②得: 2b=4
∴? b=2
? 代入②、③得:a+c=2??? ④
?????????????? 9a+c=-6?? ⑤??
⑤-④ 得:8a=-8 , ∴ a= -1
? 代入④? 得:c=3
∴? 函数的解析式为:y= -x2+2x+3解法2:(交点式)
由题意可设二次函数解析式
为 y=a(x+1)(x-3)
∵ 函数图象过点(1,4)
∴ 4 =a(1+1)(1-3) 得 a= -1
∴ 函数的解析式为:
?y= -1(x+1)(x-3) = -x2+2x+3解法3:(顶点式)
∵? 抛物线与x轴相交两点(-1,0)和(3,0) ,
∴ 对称轴为x=1
∴? 点(1,4)为抛物线的顶点
由题意设二次函数解析式为 y=a(x-1)2+4?
∵抛物线过点(-1, 0)
∴ 0=a(-1-1)2+4 得 a= -1
∴ 函数的解析式为:
y= -1(x-1)2+4= -x2+2x+3提示:
灵活应用二次函数的三种形式, 以便在用待定系数法求解二次函数解析式时减少未知数的个数, 简化运算过程,提高做题效率。已知三个点坐标三对对应值,选择一般式已知顶点坐标或对称轴或最值,选择顶点式 已知抛物线与x轴的两交点坐标,选择交点式收获! 小结 疑惑?一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。 1.我们在确定一次函数y=kx+b(k,b为常数,k≠0 )的关系式时,通常需要 个独立的条件.确定反比例函数 (k≠ 0)关系式时,通常需要 个条件.21 如果确定二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的关系式时,通常又需要 条件。3二次函数的表达式1.一般式: y=ax2+bx+c (a≠0)2.顶点式: y=a(x-h)2+k (a≠0)小组讨论合作设一般式确定二次函数表达式的基本步骤?1.设2.列3.解4. 还原(方程组)(一般形式)y=ax2+bx+c(方程组)区别巩固 顶点式
1.设y=a(x-h)2+k
2.列(方程或方程组)
3.解(方程或方程组)
4.还原(一般形式)
一般式
1.设y=ax2+bx+c
2.列(方程组)
3.解(方程组)
4. 还原(一般形式)
1、会用待定系数法确定二次函数表达式.
2、能根据抛物线上两个或三个点的坐标,确定含两个或三个未知系数的二次函数的表达式。例1(1)二次函数y=ax2+bx+c (a≠0)的图象与y轴的交点坐标
是 ;已知二次函数y=x2+2x+c 的图象过(0,-3),则
c= ,所以表达式为 。
探究新知 (3)已知二次函数的图象过点(0,-3) (1, 0)和
(-1,- 4),求这个二次函数的表达式。
(0,c)-3y= x2 + 2x-3(2)已知二次函数y=ax2+c 的图象过点(2, 3)和(0,-5),
求这个二次函数的表达式。
3=4a+c
-5=c
解: 把点(2,3),(0,-5)代入y=ax2+c得,∴二次函数的表达式为:y=2x2-5
c=-5
解之得: a=2
(3)已知二次函数的图象过点(0,-3) (1, 0)和
(-1,- 4),求这个二次函数的表达式。
学以致用 已知二次函数的图象与y轴交点的纵坐标为1,
且经过点(2,5)和(-2,13),求这个二次函数
的表达式。 解: ∵二次函数图象与y轴交点的纵坐标为1,
∴设 y=ax2+bx+1 (a≠0)
又∵图象过(2,5),(-2,13)5=4a+2b+1
13=4a-2b+1a=2
b=-2
解之得:∴y=2x2 - 2x+1∴想一想1、在什么情况下,已知二次函数图象上一点的坐标就可以确定它的表达式?
2、在什么情况下,已知二次函数图象上两点的坐标就可以确定它的表达式?
例2:解:已知抛物线的顶点为(-1,-3),且抛物线过
(-2,-5),求该抛物线的表达式?∴设二次函数表达式为:
y=a(x+1)2-3∵抛物线的顶点为(-1,-3)又点( -2,-5 )在抛物线上∴-5=a-3, 解得a= -2∴所求的抛物线表达式为 y=-2(x+1)2-3
即:y=-2x2-4x-5
已知顶点坐标,如何设二次函数的表达式?
1)顶点(1,-2) 设y= a(x )2
2) 顶点(-1,2) 设y= a(x )2
3)顶点(-1,-2) 设y= a(x )2
4)顶点 (h, k) 设y= a(x )2 -1-2+1+2+1-2- h+ k学以致用 已知二次函数的图象顶点是(-1,1),且经过点(1,-3),求这个二次函数的表达式.解:∵抛物线的顶点为(-1,1)∴设二次函数表达式为:
y=a(x+1)2+1又点( 1,-3 )在抛物线上∴4a+1=-3, 解得a=-1∴所求的抛物线表达式为 y= - (x+1)2+1
即,y= -x2-2x 1、 确定二次函数的表达式的一般步骤:知识盘点一设、二列、三解、四还原.2、确定二次函数表达式常用方法:(1)已知图象上三点或三点的对应值,通常选择一般式.
(2)已知图像的顶点坐标或对称轴和最值,通常选择顶点式. 选择最优解法,求下列二次函数表达式:
1.(必做)已知抛物线的图象经过点(1,1)、(-1,-1)、(0,-2),设抛物线解析式为_______ ___.
2.(必做) 已知抛物线的顶点坐标(-2,3) ,且经过点(-1,0) ,设抛物线解析式为_________ ___.
3.(选做)已知二次函数有最大值6,且经过点(2, 3),(-4,5),设抛物线解析式为___ __ ____.
4.(选做)已知抛物线的对称轴是直线x=-2,且经过点(1,3),(5,6),设抛物线解析式为_____ ___.达标测试y=ax2+bx+c(a≠0)y=a(x+2)2+3(a≠0)y=a(x-h)2+6(a≠0)y=a(x+2)2+k(a≠0)作业布置必做题:习题2.6的1、2题;
选做题:习题2.6的3题。-x1- x2求出下表中抛物线与x轴的交点坐标,看看你有什么发现?(1,0)(3,0)(2,0)(-1,0)(-4,0)(-6,0)(x1,0),( x2,0)y=a(x___)(x____)
(a≠0)探究二次函数解析式-x1- x2求出下表中抛物线与x轴的交点坐标,看看你有什么发现?(1,0)(3,0)(2,0)(-1,0)(-4,0)(-6,0)(x1,0),( x2,0)y=a(x___)(x____)
(a≠0)交点式探究二次函数解析式y=a(x-1)(x-3)(a≠0)y=a(x-2)(x+1)(a≠0)y=a(x+4)(x+6)(a≠0)已知三个点坐标,选择一般式已知顶点坐标或对称轴或最值,选择顶点式 已知抛物线与x轴的两交点坐标,选择交点式二次函数常用的三种解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。 例题?已知二次函数图象经过点(1,4),(-1,0)和(3,0)三点,求二次函数的解析式.解法1:(一般式)
设二次函数解析式为y=ax2+bx+c
∵二次函数图象过点(1,4),(-1,0)和(3,0)
∴? a+b+c=4?????? ①
??? a-b+c=0?????? ②
?? 9a+3b+c=0??? ? ③
①-②得: 2b=4
∴? b=2
? 代入②、③得:a+c=2??? ④
?????????????? 9a+c=-6?? ⑤??
⑤-④ 得:8a=-8 , ∴ a= -1
? 代入④? 得:c=3
∴? 函数的解析式为:y= -x2+2x+3解法2:(交点式)
由题意可设二次函数解析式
为 y=a(x+1)(x-3)
∵ 函数图象过点(1,4)
∴ 4 =a(1+1)(1-3) 得 a= -1
∴ 函数的解析式为:
?y= -1(x+1)(x-3) = -x2+2x+3解法3:(顶点式)
∵? 抛物线与x轴相交两点(-1,0)和(3,0) ,
∴ 对称轴为x=1
∴? 点(1,4)为抛物线的顶点
由题意设二次函数解析式为 y=a(x-1)2+4?
∵抛物线过点(-1, 0)
∴ 0=a(-1-1)2+4 得 a= -1
∴ 函数的解析式为:
y= -1(x-1)2+4= -x2+2x+3提示:
灵活应用二次函数的三种形式, 以便在用待定系数法求解二次函数解析式时减少未知数的个数, 简化运算过程,提高做题效率。已知三个点坐标三对对应值,选择一般式已知顶点坐标或对称轴或最值,选择顶点式 已知抛物线与x轴的两交点坐标,选择交点式收获! 小结 疑惑?一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。 1.我们在确定一次函数y=kx+b(k,b为常数,k≠0 )的关系式时,通常需要 个独立的条件.确定反比例函数 (k≠ 0)关系式时,通常需要 个条件.21 如果确定二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的关系式时,通常又需要 条件。3二次函数的表达式1.一般式: y=ax2+bx+c (a≠0)2.顶点式: y=a(x-h)2+k (a≠0)小组讨论合作设一般式确定二次函数表达式的基本步骤?1.设2.列3.解4. 还原(方程组)(一般形式)y=ax2+bx+c(方程组)区别巩固 顶点式
1.设y=a(x-h)2+k
2.列(方程或方程组)
3.解(方程或方程组)
4.还原(一般形式)
一般式
1.设y=ax2+bx+c
2.列(方程组)
3.解(方程组)
4. 还原(一般形式)
