数学九年级上青岛版3.1圆的对称性课件6
文档属性
| 名称 | 数学九年级上青岛版3.1圆的对称性课件6 |
|
|
| 格式 | zip | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 00:00:00 | ||
图片预览




文档简介
课件47张PPT。§5.2.2 圆的对称性(二)垂径定理(2)二、垂径定理:一、圆是轴对称图形,其对称轴是 垂直于弦的直径平分这条弦,并且平分弦所对的弧.
三、垂径定理和勾股定理相结合,构造
直角三角形,可解决计算弦长、半
径、弦心距等问题.
任意一
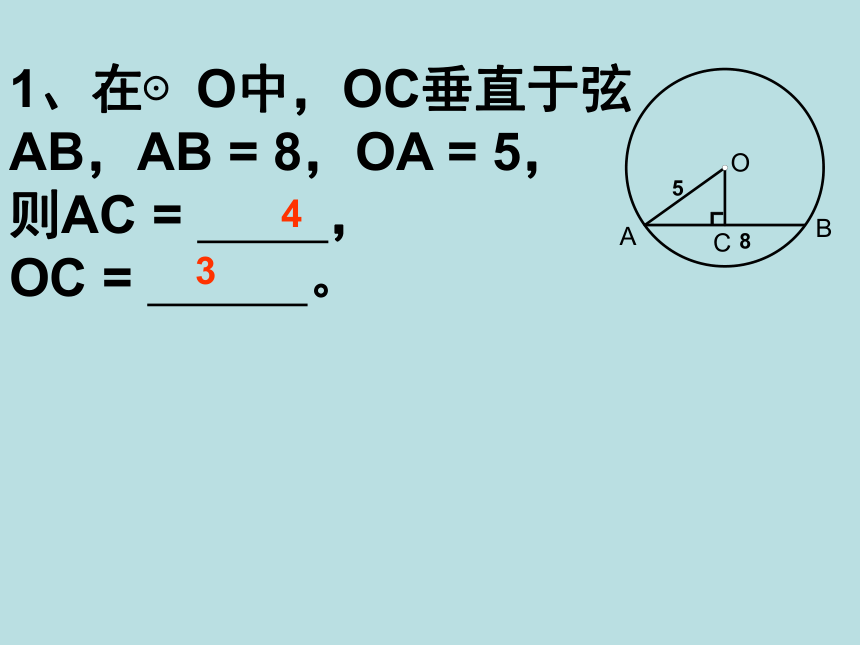
条过圆心的直线(或直径所在直线.)复习EABO弦的一半半径弦心距弦的一半2+弦心距2=半径2∟要求弦,只需求弦的一半,常作垂直于弦的半径,构成直角三角形.要求半径, 常作弦心距,构成直角三角形.1、在⊙O中,OC垂直于弦AB,AB = 8,OA = 5,
则AC = ,
OC = 。┏58432. 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,CM = 4,求AB。
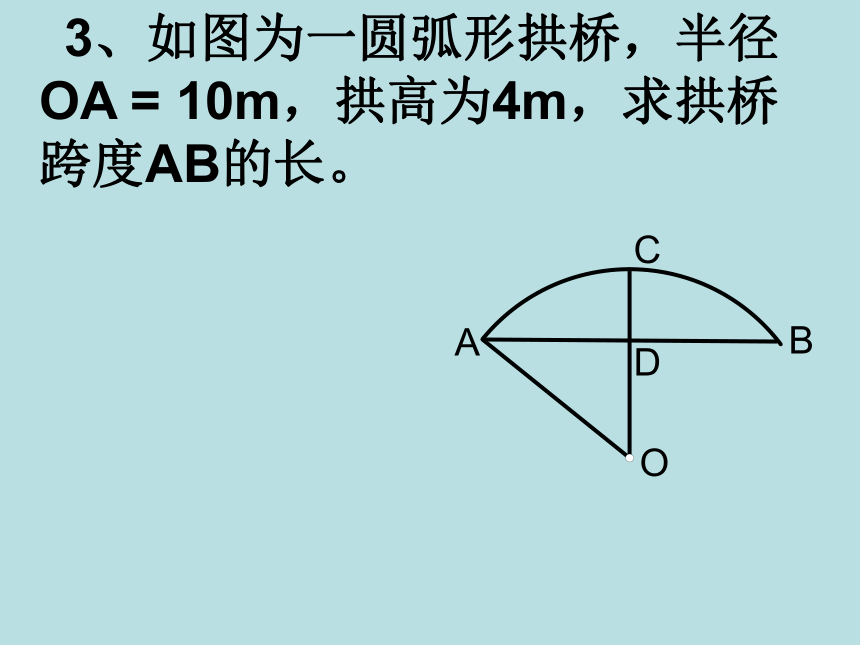
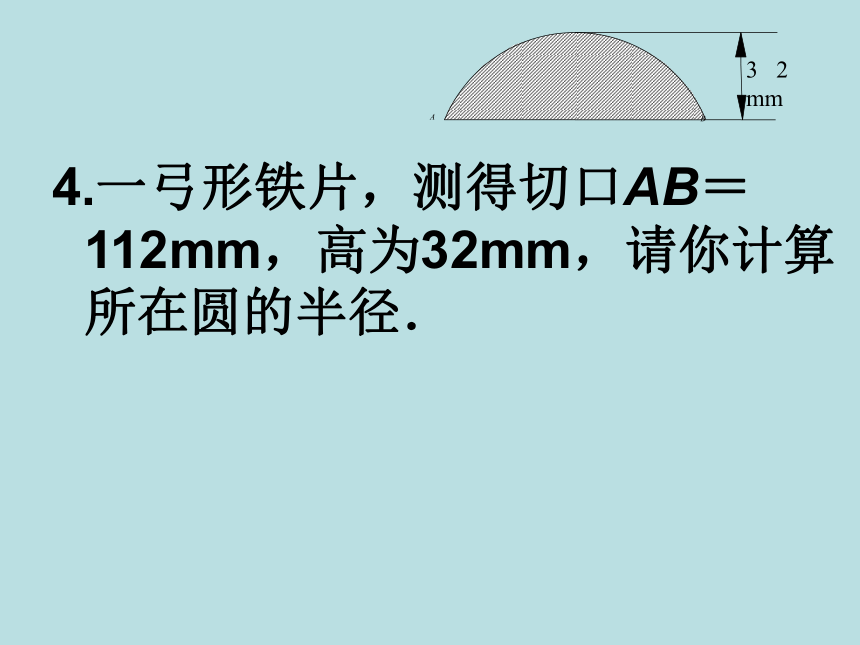
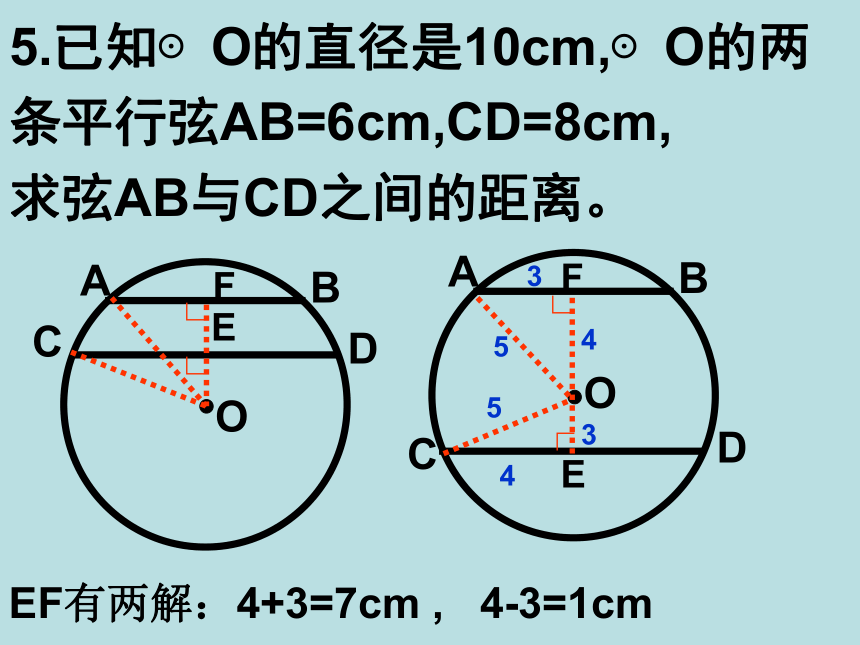
解:连接OA在⊙O中,直径CD⊥弦AB∴ AB =2AM△OMA是Rt △∵ CD = 20∴ AO = CO = 10∴ OM = OC – CM = 10 – 4 = 6在Rt △OMA中,AO = 10,OM = 6根据勾股定理,得:∴∴ AB = 2AM = 2 x 8 = 163、如图为一圆弧形拱桥,半径OA = 10m,拱高为4m,求拱桥跨度AB的长。 4.一弓形铁片,测得切口AB=112mm,高为32mm,请你计算所在圆的半径.5.已知⊙O的直径是10cm,⊙O的两条平行弦AB=6cm,CD=8cm,
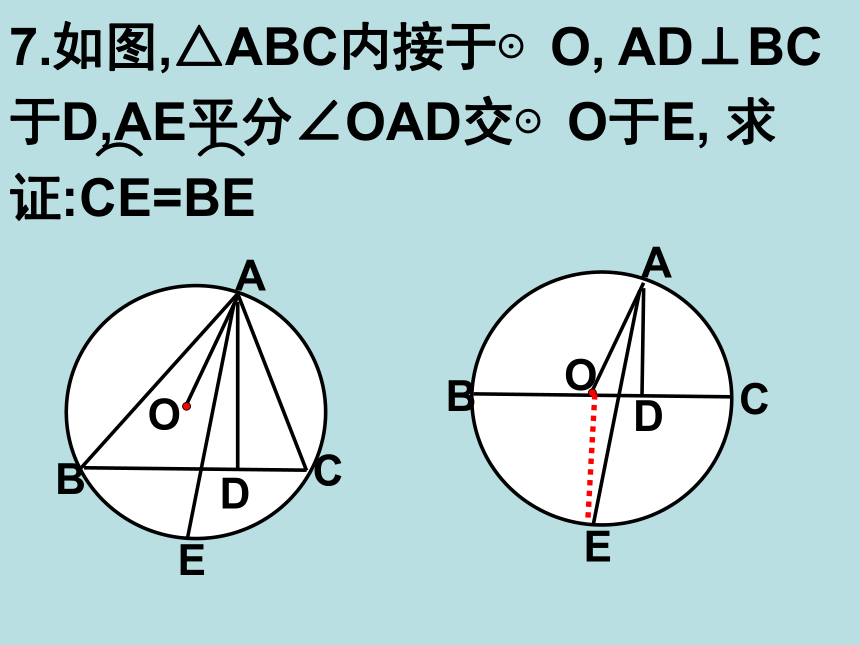
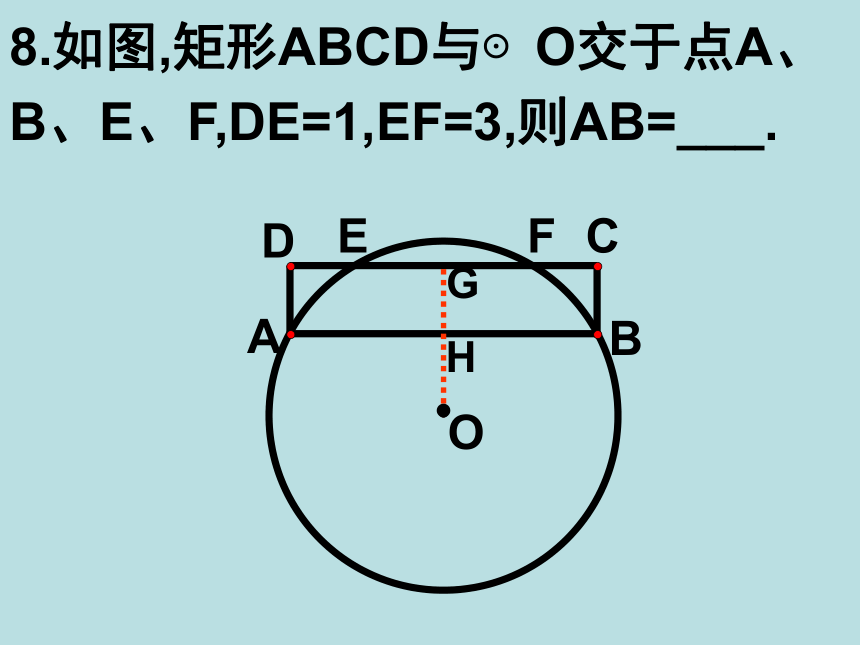
求弦AB与CD之间的距离。 345543EF有两解:4+3=7cm , 4-3=1cm6. 储油罐的截面直径为650mm,装入一些油后,测得油面的宽度AB=600mm,求油的深度.ADOECB7.如图,△ABC内接于⊙O, AD⊥BC于D,AE平分∠OAD交⊙O于E, 求证:CE=BE⌒⌒8.如图,矩形ABCD与⊙O交于点A、B、E、F,DE=1,EF=3,则AB=___.FEDCBAO9.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.MN复习:∵在⊙O中,CD是直径,∴ AP=BP, 垂直于弦的直径,
平分这条弦
并且平分弦所对的两条弧。(垂径定理)AP你可以写出相应的命题吗?如图,在下列五个条件中:只要具备其中两个条件,
就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,垂 径 定 理 的 逆 定 理②CD⊥AB,AB是⊙O的一条弦,且AP=BP.过点P作直径CD.由 ① CD是直径③ AP=BP┗平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.垂 径 定 理 的 逆 定 理垂 径 定 理 的 逆 定 理弦(不是直径)并且平分弦所对的弧 平分的直径垂直于弦,?!②CD⊥AB,垂径定理的逆定理AB是⊙O的一条弦,且AP=BP.过点P作直径CD.由 ① CD是直径③ AP=BP┗平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.练:在⊙O中,OC平分弦AB,AB = 16,OA = 10,则∠OCA = °,
OC = 。1610906由②CD⊥AB,垂径定理的逆定理AB是⊙O的一条弦,且AP=BP.过点P作直径CD.③ AP=BP┗① CD是直径弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 推论1:
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
垂径定理及逆定理垂直于弦的直径平分弦,并且平分弦所的两条弧.平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.① CD是直径,③ AM=BM,② CD⊥AB,如图,⊙O直径CD与弦AB(非直径)交于点M,添加一个条件:____,就可得到点M是AB的中点.拓展如图,AB,CD是⊙O的两条平行弦,AC与BD相等吗?为什么?⌒⌒如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?圆的两条平行弦所夹的弧相等垂径定理的推论 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?提示: 这两条弦在圆中位置有两种情况:圆的两条平行弦所夹的弧相等.垂径定理
的推论例1.判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???练习(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。???挑战自我填一填1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )2.已知:如图,⊙O 中,弦AB∥CD,AB<CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有:
.
图中相等的劣弧有:
.3.平分已知AB⌒CDABE例:平分已知弧AB已知:弧AB
作法:⒈ 连结AB.⒉作AB的垂直平分线CD,交弧AB于点E.点E就是所求弧AB的中点。求作:弧AB的中点CDABEFG变式一: 求弧AB的四等分点。 mnCDABMTEFGHNP错在哪里?等分弧时一定要作弧所夹弦的垂直平分线。●作AB的垂直平分线CD。●作AT.BT的垂直
平分线EF.GHCABE变式二:你能确定 弧AB的圆心吗?mnDCABEmnO你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据:5.如图,已知⊙O的半径r=5cm,弦AB=6cm,D是AB的中点,求弦BD⌒D6.如图,AB、AC为弦,OM⊥AB于M,ON⊥AC于N,BC=4,求MN的长..ACOMNB7.⊙O1与⊙O2相交于A、B两点,过点A作O1O2的平行线,与两圆相交于点C、D,试猜想CD与O1O2的关系. MN8.如图,AB是⊙O的直径,CD是⊙O的弦,MC⊥CD, ND⊥CD,分别交AB于M、N,AM与BN大小怎样?CDOABNMLL10.如图,点A是半圆上的三等分点,B是弧AN的中点,P是直径MN上一动点,圆O的半径是1,问AP+PB的最小值.ABPMNO11.将一直径为17cm的圆形纸片(图①)剪成如图②所示形状的纸片,再将纸片沿虚线折叠得到正方体(图③)纸盒,则这样的纸盒体积最大为__cm3.8.5X4X12.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为___.ABCO∟∟13.如图,有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?AEBMFNH3.6X小结垂径定理垂直于弦的直径平分弦,并且平分弦所的两条弧.垂径定理的逆定理 平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧. 平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧. 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
三、垂径定理和勾股定理相结合,构造
直角三角形,可解决计算弦长、半
径、弦心距等问题.
任意一
条过圆心的直线(或直径所在直线.)复习EABO弦的一半半径弦心距弦的一半2+弦心距2=半径2∟要求弦,只需求弦的一半,常作垂直于弦的半径,构成直角三角形.要求半径, 常作弦心距,构成直角三角形.1、在⊙O中,OC垂直于弦AB,AB = 8,OA = 5,
则AC = ,
OC = 。┏58432. 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,CM = 4,求AB。
解:连接OA在⊙O中,直径CD⊥弦AB∴ AB =2AM△OMA是Rt △∵ CD = 20∴ AO = CO = 10∴ OM = OC – CM = 10 – 4 = 6在Rt △OMA中,AO = 10,OM = 6根据勾股定理,得:∴∴ AB = 2AM = 2 x 8 = 163、如图为一圆弧形拱桥,半径OA = 10m,拱高为4m,求拱桥跨度AB的长。 4.一弓形铁片,测得切口AB=112mm,高为32mm,请你计算所在圆的半径.5.已知⊙O的直径是10cm,⊙O的两条平行弦AB=6cm,CD=8cm,
求弦AB与CD之间的距离。 345543EF有两解:4+3=7cm , 4-3=1cm6. 储油罐的截面直径为650mm,装入一些油后,测得油面的宽度AB=600mm,求油的深度.ADOECB7.如图,△ABC内接于⊙O, AD⊥BC于D,AE平分∠OAD交⊙O于E, 求证:CE=BE⌒⌒8.如图,矩形ABCD与⊙O交于点A、B、E、F,DE=1,EF=3,则AB=___.FEDCBAO9.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.MN复习:∵在⊙O中,CD是直径,∴ AP=BP, 垂直于弦的直径,
平分这条弦
并且平分弦所对的两条弧。(垂径定理)AP你可以写出相应的命题吗?如图,在下列五个条件中:只要具备其中两个条件,
就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,垂 径 定 理 的 逆 定 理②CD⊥AB,AB是⊙O的一条弦,且AP=BP.过点P作直径CD.由 ① CD是直径③ AP=BP┗平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.垂 径 定 理 的 逆 定 理垂 径 定 理 的 逆 定 理弦(不是直径)并且平分弦所对的弧 平分的直径垂直于弦,?!②CD⊥AB,垂径定理的逆定理AB是⊙O的一条弦,且AP=BP.过点P作直径CD.由 ① CD是直径③ AP=BP┗平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.练:在⊙O中,OC平分弦AB,AB = 16,OA = 10,则∠OCA = °,
OC = 。1610906由②CD⊥AB,垂径定理的逆定理AB是⊙O的一条弦,且AP=BP.过点P作直径CD.③ AP=BP┗① CD是直径弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 推论1:
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
垂径定理及逆定理垂直于弦的直径平分弦,并且平分弦所的两条弧.平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.① CD是直径,③ AM=BM,② CD⊥AB,如图,⊙O直径CD与弦AB(非直径)交于点M,添加一个条件:____,就可得到点M是AB的中点.拓展如图,AB,CD是⊙O的两条平行弦,AC与BD相等吗?为什么?⌒⌒如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?圆的两条平行弦所夹的弧相等垂径定理的推论 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?提示: 这两条弦在圆中位置有两种情况:圆的两条平行弦所夹的弧相等.垂径定理
的推论例1.判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???练习(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。???挑战自我填一填1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )2.已知:如图,⊙O 中,弦AB∥CD,AB<CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有:
.
图中相等的劣弧有:
.3.平分已知AB⌒CDABE例:平分已知弧AB已知:弧AB
作法:⒈ 连结AB.⒉作AB的垂直平分线CD,交弧AB于点E.点E就是所求弧AB的中点。求作:弧AB的中点CDABEFG变式一: 求弧AB的四等分点。 mnCDABMTEFGHNP错在哪里?等分弧时一定要作弧所夹弦的垂直平分线。●作AB的垂直平分线CD。●作AT.BT的垂直
平分线EF.GHCABE变式二:你能确定 弧AB的圆心吗?mnDCABEmnO你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据:5.如图,已知⊙O的半径r=5cm,弦AB=6cm,D是AB的中点,求弦BD⌒D6.如图,AB、AC为弦,OM⊥AB于M,ON⊥AC于N,BC=4,求MN的长..ACOMNB7.⊙O1与⊙O2相交于A、B两点,过点A作O1O2的平行线,与两圆相交于点C、D,试猜想CD与O1O2的关系. MN8.如图,AB是⊙O的直径,CD是⊙O的弦,MC⊥CD, ND⊥CD,分别交AB于M、N,AM与BN大小怎样?CDOABNMLL10.如图,点A是半圆上的三等分点,B是弧AN的中点,P是直径MN上一动点,圆O的半径是1,问AP+PB的最小值.ABPMNO11.将一直径为17cm的圆形纸片(图①)剪成如图②所示形状的纸片,再将纸片沿虚线折叠得到正方体(图③)纸盒,则这样的纸盒体积最大为__cm3.8.5X4X12.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为___.ABCO∟∟13.如图,有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?AEBMFNH3.6X小结垂径定理垂直于弦的直径平分弦,并且平分弦所的两条弧.垂径定理的逆定理 平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧. 平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧. 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
