数学九年级上青岛版3.3圆周角课件3

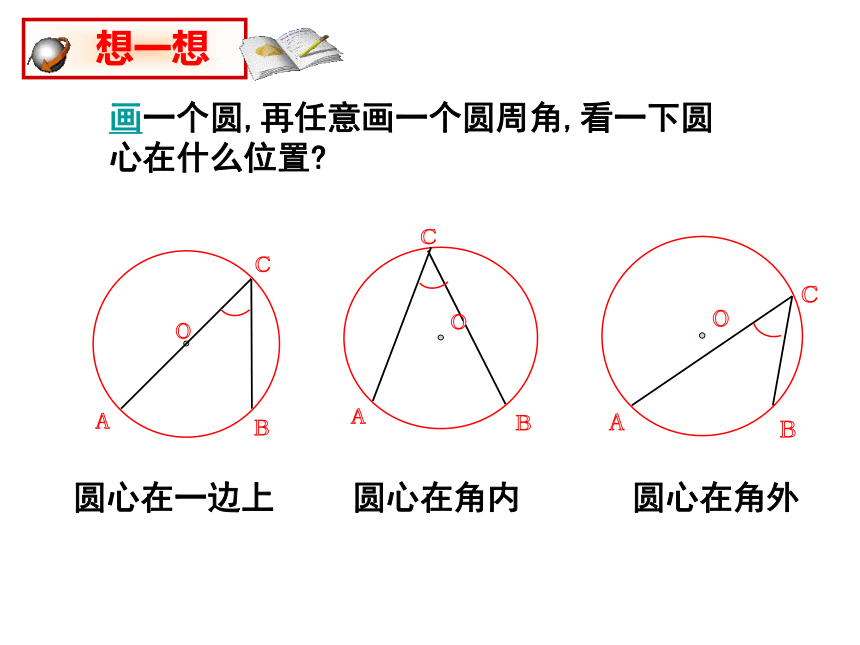
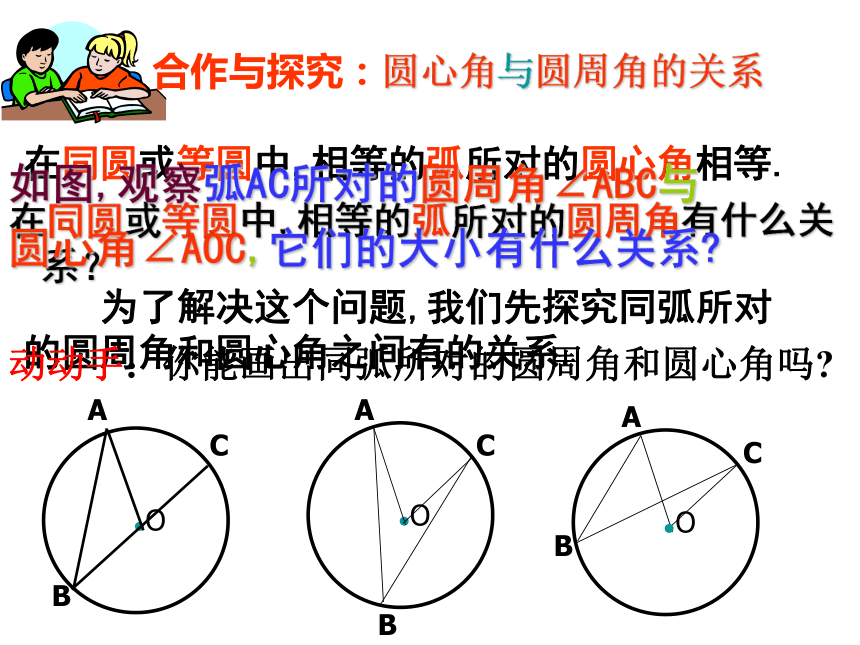
课件29张PPT。3.3 圆周角1.圆心角、圆周角的定义?相 等.顶点在圆心的角叫圆心角.3.圆心角的度数和它所对的弧的度数的关系?顶点在圆上，并且两边与圆相交的角叫圆周角。2.圆心角与他对的弦、弧的关系?用于判断某个圆周角是否是直角用于判断某条线是否过圆心90°的圆周角所对的弦是直径。 想一想半圆（或直径）所对的圆周角是直角；画一个圆,再任意画一个圆周角,看一下圆心在什么位置?圆心在一边上圆心在角内圆心在角外 想一想在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系？ 为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.合作与探究：圆心角与圆周角的关系如图,观察弧AC所对的圆周角∠ABC与
圆心角∠AOC,它们的大小有什么关系?动动手：你能画出同弧所对的圆周角和圆心角吗?1.首先考虑一种特殊情况：
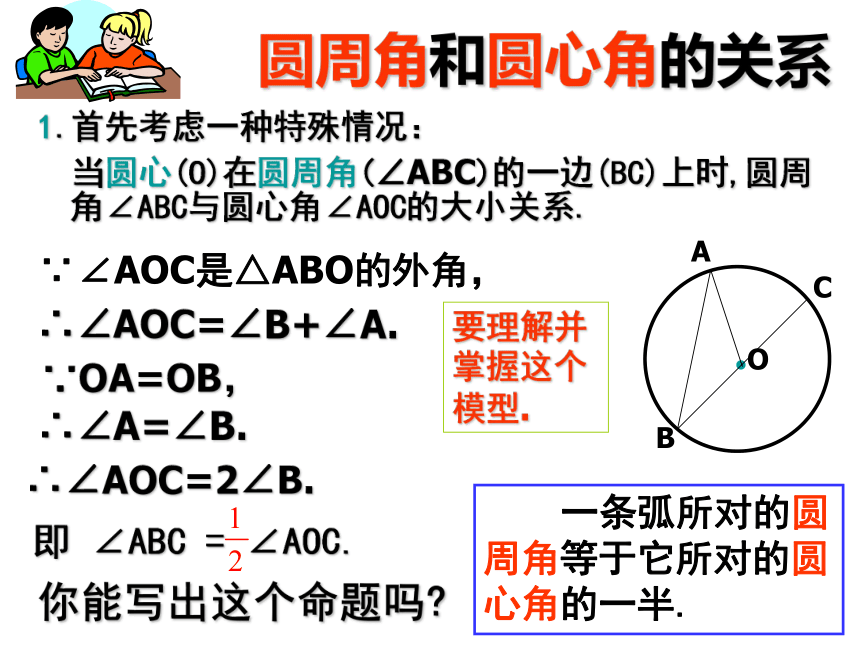
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角，∴∠AOC=∠B+∠A.∵OA=OB，∴∠A=∠B.∴∠AOC=2∠B.即 ∠ABC = ∠AOC.你能写出这个命题吗? 一条弧所对的圆周角等于它所对的圆心角的一半.要理解并掌握这个模型.圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?
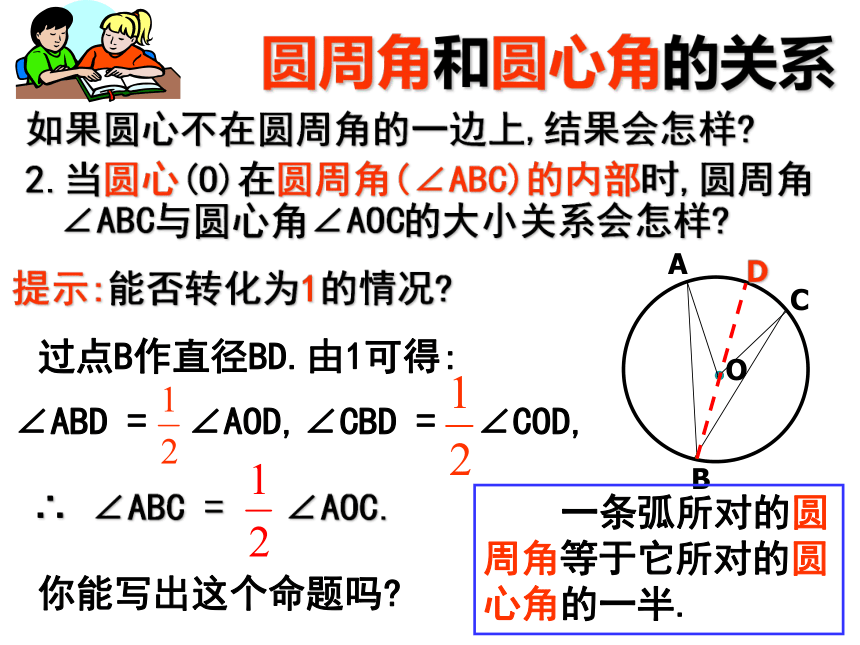
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?提示:能否转化为1的情况?过点B作直径BD.由1可得: ∴ ∠ABC = ∠AOC.你能写出这个命题吗?∠ABD = ∠AOD,∠CBD = ∠COD,圆周角和圆心角的关系 一条弧所对的圆周角等于它所对的圆心角的一半.如果圆心不在圆周角的一边上,结果会怎样?
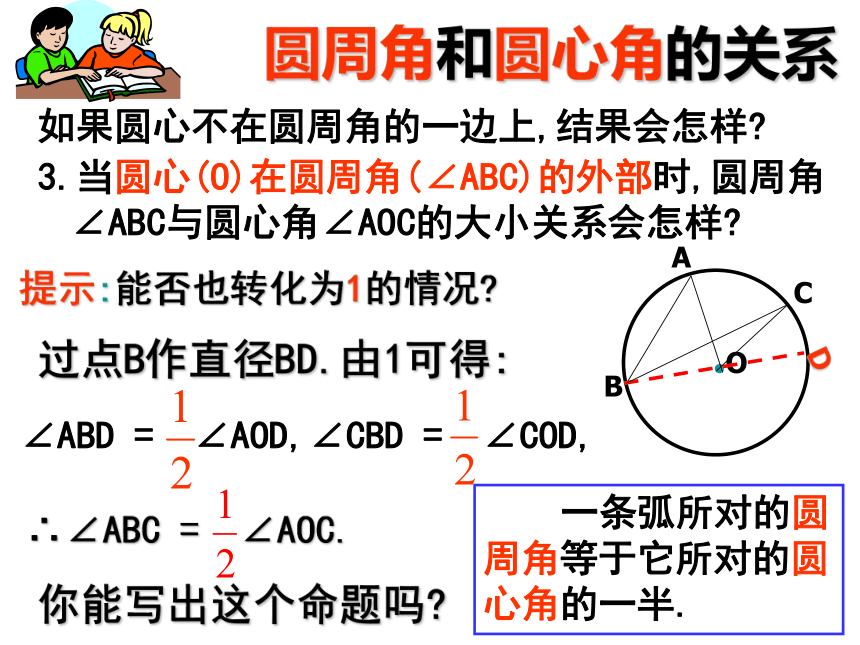
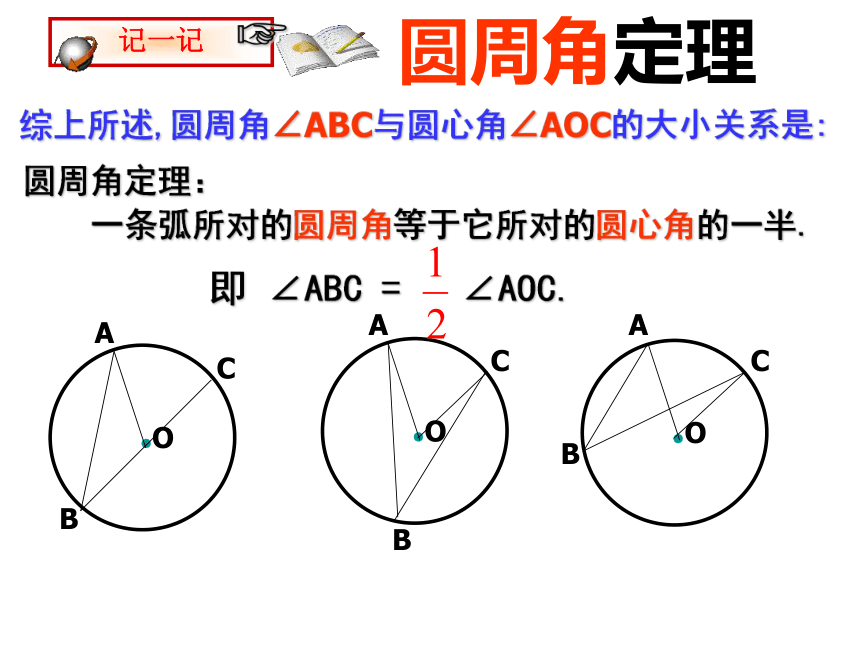
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?提示:能否也转化为1的情况?过点B作直径BD.由1可得:∴∠ABC = ∠AOC.你能写出这个命题吗?∠ABD = ∠AOD,∠CBD = ∠COD,圆周角和圆心角的关系 一条弧所对的圆周角等于它所对的圆心角的一半.圆周角定理综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:圆周角定理：
一条弧所对的圆周角等于它所对的圆心角的一半.即 ∠ABC = ∠AOC.观察与思考？问题1：如图,在⊙O中,∠ABC,∠ADC,∠AEC 的大小有什么关系?为什么?∠ABC = ∠ADC= ∠AEC 若已知∠BEA与∠ADC，你又会得到什么结论？为什么？规律：同弧或等弧所对的圆周角相等。相等的圆周角所对的弧相等。 思考：在等圆中上述结论成立吗？问题：在半径不等的圆中，相等的两个圆周角所对的弧相等吗？
如图，∠ABC=30°，∠A′B′C′=30°，但是弧AC 与A′C′不等观察与思考？规律：同弧或等弧所对的圆周角相等。在同圆或等圆中相等的圆周角所对的弧相等。∠ACB的度数与它所对的弧AB的度数有什么关系?分析:连接OA,OB,∴ ∠ACB的度数等于它所
对的弧AB的度数的一半.规律：
圆周角的度数等于它所对的弧的度数的一半观察与思考？ABDC如图:四边形ABCD中,∠A 与 ∠C有何关系?∠A +∠C=180驶向胜利的彼岸 规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理例1.如图：OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.
求证：∠ACB=2∠BAC.证明：∠ACB= ∠AOB12∠BAC= ∠BOC2∠AOB=2∠BOC∠ACB=2∠BAC1 ⌒例题　2、在⊙O中，∠CBD=30° ,∠BDC=20°,求∠A所以∠CDB= ∠CAB=20所以∠DAB=50°°　1、在⊙O中，∠CBD=30° ,∠BDC=20°,求∠A　3、如图，在⊙O中，AB为直径，CB = CF,
弦CG⊥AB，交AB于D，交BF于E
求证：BE=EC
例题⌒⌒例 4. 如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．又在Rt△ABD中，AD2+BD2=AB2，解：∵AB是直径，∴ ∠ACB= ∠ADB=90°．在Rt△ABC中，∵CD平分∠ACB，∴AD=BD.例5. 在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻，当甲带球冲到A点时，乙已跟随冲到B点(如图2)．此时甲是自己直接射门好，还是迅速将球回传给乙，让乙射门好？分析 在真正的足球比赛中情况会很复杂，这里仅用数学方法从两点的静止状态加以考虑，如果两个点到球门的距离相差不大，要确定较好的射门位置，关键看这两个点分别对球门MN的张角大小，当张角较小时，则球容易被对方守门员拦截.怎样比较A、B两点对MN张角的大小呢？解 考虑过M、N以及A、B中的任一点作一圆，这里不妨作出⊙BMN，显然，A点在⊙BMN外，设MA交圆于C，则 ∠MAN＜∠MCN，而∠MCN=∠MBN，
　　所以∠MAN＜∠MBN．
　　因此，甲应将球回传给乙，让乙射门. ·o(1)当船与两个灯塔的夹角∠α大于
“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小
于“危险角”时,船位于哪个区域?
为什么?例6.船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图所示,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁. ·o答(1)船位于暗礁区域内(即圆o内).
理由:假设船在⊙O上,则有∠α=∠C,这与
∠α＞ ∠ C矛盾.所以船不可能在⊙O上;
假设船在⊙O外,则有∠ α＜ ∠AEB,即
∠ α ＜ ∠C,这与∠ α ＞ ∠C矛盾.
所以:
船不可能在⊙O外.
因此,船只能位于⊙O内.(2)船位于暗礁区域外(即⊙O外).拓展 化心动为行动1.如图(1),在⊙O中,∠BAD=50°,求∠C的大小.2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
3.如图(3),AB是直径,你能确定∠C的度数吗?1.如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？ABCD12345678∠1 = ∠4∠5 = ∠8∠2 = ∠7∠3 = ∠6练 习2.AB、AC为⊙O的两条弦，延长CA到D，使 AD=AB，如果∠ADB=35° ，
求∠BOC的度数。∠BOC =140° ∠A=21° 练 习5、在⊙O中，一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°，则x=_ _；4. 如图，在直径为AB的半圆中，O为圆心，C、D
为半圆上的两点，∠COD=50°，则
∠CAD=______；20°25°6.如图，你能设法确定一个圆形纸片的圆心吗？你有多少种方法？与同学交流一下．DOOO·方法一方法二方法三方法四AB1、圆周角定理的推论1：同圆或等圆中，同弧或等弧所对的圆周角相等；
同圆或等圆中，相等的圆周角所对的弧也相等。2、圆周角定理的推论2：用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心半圆（或直径）所对的圆周角是直角；
90°的圆周角所对的弦是直径。 想一想1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.3.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。2.半圆或直径所对的圆周角都相等，都等于90°
90°的圆周角所对的弦是圆的直径小结: