数学九年级上青岛版3.5三角形的内切圆课件6
文档属性
| 名称 | 数学九年级上青岛版3.5三角形的内切圆课件6 |
|
|
| 格式 | zip | ||
| 文件大小 | 178.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 00:00:00 | ||
图片预览





文档简介
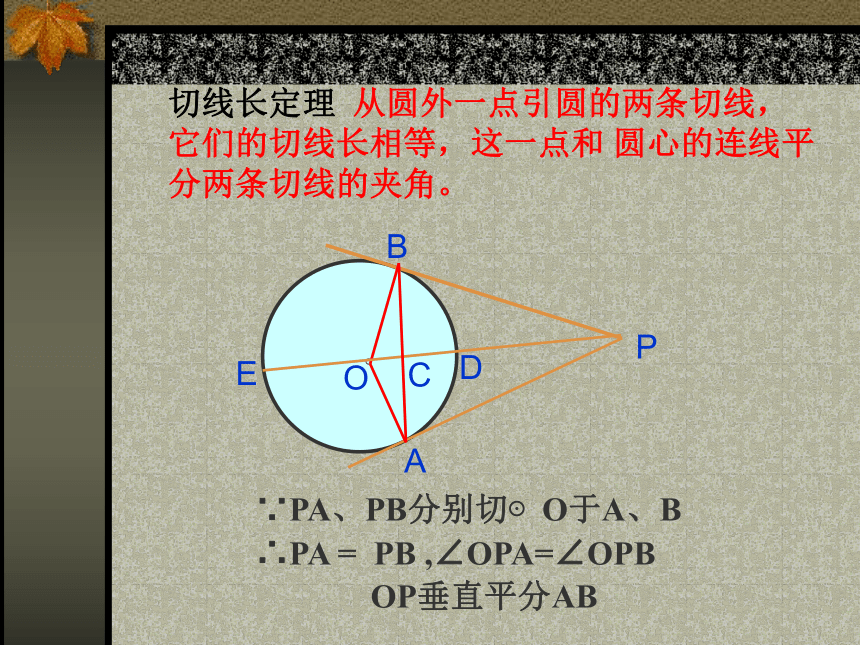
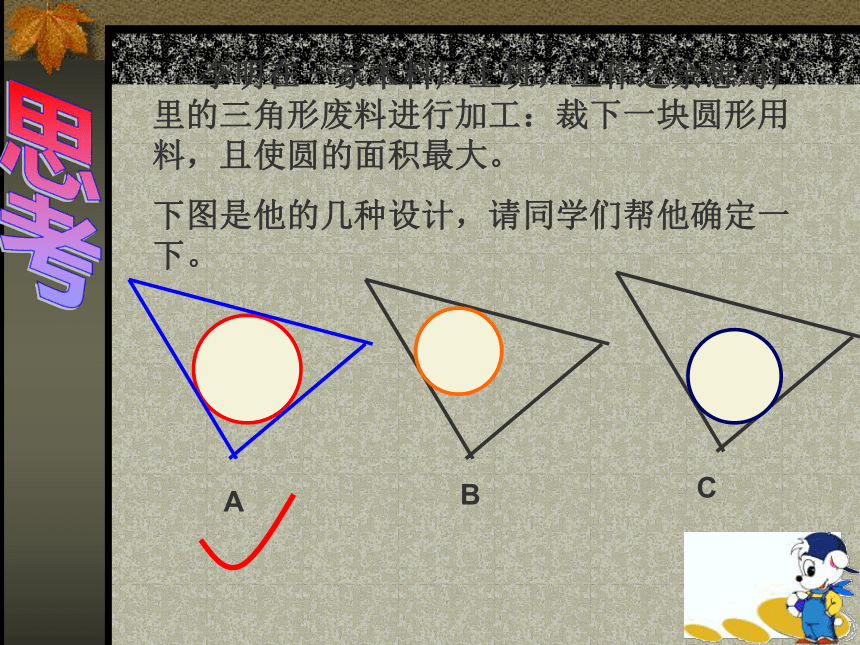
课件28张PPT。三角形的内切圆CBAOr课 题切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,这一点和 圆心的连线平分两条切线的夹角。 ∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPBOP垂直平分AB1、确定圆的条件是什么?1.圆心与半径2、叙述角平线的性质与判定性质:角平线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。3、下图中△ABC与圆O的关系?△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心知识回顾ACBO2.不在同一直线上的三点 李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。
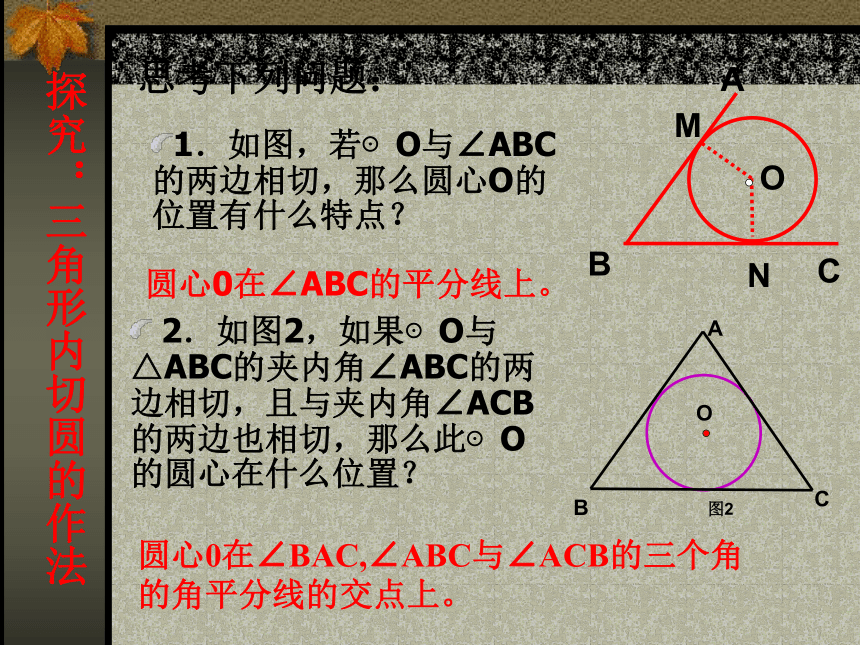
下图是他的几种设计,请同学们帮他确定一下。思考ABC思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的夹内角∠ABC的两边相切,且与夹内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法3.如何确定一个与三角形的三边都相切的圆心的位置与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆么? 作出三个内角的平分线,三条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径。 只能作一个,因为三角形的三条内角
平分线相交只有一个交点。 IFCABED探究:三角形内切圆的作法作法: ABC1、作∠B、∠C的平分线BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN探究:三角形内切圆的作法1、定义:和三角形各边都相切的圆叫做三角 形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。识记2、性质: 内心到三角形三边的距离相等;
内心与顶点连线平分内角。3、和多边形各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形。三角形的外心与内心对照画出的图形,讨论解决下列问题:
1、什么是三角形的外心与内心?
2、试比较三角形的外心与内心的区别,并填表:外心是指三角形外接圆的圆心内心是指三角形内切圆的圆心三角形各边垂直平分线的交点到三角形各顶点的距离相等三角形各内角角平分线的交点到三角形各边的距离相等例题1:如图,在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的
度数。 分析: ∠O = ? ∠1 + ∠3= ? O为△ABC的内心 BO是∠ABC的角平分线 CO是∠ACB的角平分线 三角形内心性质的应用解: ∵点O为△ABC的内心 ∴∠1=∠2= ∴ ∠BOC=1800 - (∠1+∠3)
=1800 - (250+37.50)
=117.50
∴ ∠BOC=117.50
C三角形内心性质的应用延伸与拓展如图,在△ABC中,∠A=n°,点I是内心,求∠BIC的度数。解:∠BIC=1800-(∠IBC+∠ICB)
=1800-=1800-=1800-900+=900+一般地: △ABC的内心为I, ∠A=n0
则∠BIC=900+例2、求等边三角形的内切圆半径r与
外接圆半径R的比。解:由等腰三角形底边上的中垂线与顶角平分线重合的性质知,等边三角形的内切圆与外接圆是两个同心圆设内切圆切BC于D,连接OB,OD于是就有sin∠OBD=sin30°=
知 识 的 应 用·BDEFOCA如图,△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.解:设△ABC的内切圆与三边相切于D、E、F,连结OA、OB、OC、OD、OE、OF,则OD⊥AB,OE⊥BC,OF⊥AC.∴S△ABC=S△AOB+S△BOC +S△AOC= AB·OD+ BC·OE+ AC·OF= l·r设△ABC的三边为a、b、c,面积为S,
则△ABC的内切圆的半径 r=结论三角形的内切圆的有关计算·ABCEDFO如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.设AD= x , BE= y ,CE= r ∵ ⊙O与Rt△ABC的三边都相切∴AD=AF,BE=BF,CE=CD解:设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OD⊥AC,OE⊥BC,OF⊥AB。结论r如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。如图:直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径为:2cm练习·ABCEDFO如图,Rt△ABC中,∠C=90°,BC=3,AC=4, ⊙O为Rt△ABC的内切圆. (1)求Rt△ABC的内切圆的半径 . (2)若移动点O的位置,使⊙O保持与△ABC的边AC、BC都相切,求⊙O的半径r的取值范围。设AD= x , BE= y ,CE= r ∵ ⊙O与Rt△ABC的三边都相切∴AD=AF,BE=BF,CE=CD解:(1)设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。解得r=1在Rt△ABC中,BC=3,AC=4, ∴AB=5由已知可得四边形ODCE为正方形,∴CD=CE=OD∴ Rt△ABC的内切圆的半径为1。(2)如图所示,设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连结OB、OD,则四边形BODC为正方形。·ABODC∴OB=BC=3∴半径r的取值范围为0<r≤3点评几何问题代数化是解决几何问题的一种重要方法。例.如图,△ABC中,∠C =90o ,它的
内切圆O分别与边AB、BC、CA相切
于点D、E、F,且BD=12,AD=8,
求⊙O的半径r.
基础题:1.既有外接圆,又内切圆的平行四边形是______.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O是边长为2cm的正方形ABCD的内切圆,EF切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.EFHG正方形22cm2cm 1、如图,四边形ABCD的边 AB,BC,CD,DA和⊙O分别相切于L,M,N,P。
(1)图中有几对相等的线段?(2)由此你能发现什么结论? 为什么?∵ AB,BC,CD,DA都与⊙O相切,L,M,N,P是切点,∴AL=AP,LB=MB,
DN=DP,NC=MC∴AL+ LB+ DN+ NC = AP+ MB+DP+MC即 AB+ CD = AD+BC圆的外切四边形的两组对边的和相等延伸与拓展2、圆内接平行四边形是矩形圆外切平行四边形是_______延伸与拓展菱形3、圆内接梯形为等腰梯形4、已知圆外切等腰梯形的中位线长
为3cm,则腰长为____3cm延伸与拓展8cm6cm4cm6cm课堂练习1、判断:
如图:1、△ABC是圆D的外切三角形。( )
2、圆D是△ABC的外接圆。 ( )
3、△ABC是圆O的外接三角形。 ( )
2、到三角形三边距离相等的点是三角形的( )
A、内心 B、外心
3、一个直角三角形的斜边的长为10cm,内切圆的半径为1cm,则三角形的周长是-------------- ABCDO检测4.已知:△ABC中,E是内心,∠A的平 分线和△ABC的外接圆相交于点D,
求证:DE=DB=DC
ABCDE补充练习4.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出锅盖的直径,请你利用图乙,说
明她这样做的道理.同学们要好好学习老师期盼你们快快进步!
判定:到这个角的两边距离相等的点在这个角的平分线上。3、下图中△ABC与圆O的关系?△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心知识回顾ACBO2.不在同一直线上的三点 李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。
下图是他的几种设计,请同学们帮他确定一下。思考ABC思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的夹内角∠ABC的两边相切,且与夹内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法3.如何确定一个与三角形的三边都相切的圆心的位置与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆么? 作出三个内角的平分线,三条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径。 只能作一个,因为三角形的三条内角
平分线相交只有一个交点。 IFCABED探究:三角形内切圆的作法作法: ABC1、作∠B、∠C的平分线BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN探究:三角形内切圆的作法1、定义:和三角形各边都相切的圆叫做三角 形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。识记2、性质: 内心到三角形三边的距离相等;
内心与顶点连线平分内角。3、和多边形各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形。三角形的外心与内心对照画出的图形,讨论解决下列问题:
1、什么是三角形的外心与内心?
2、试比较三角形的外心与内心的区别,并填表:外心是指三角形外接圆的圆心内心是指三角形内切圆的圆心三角形各边垂直平分线的交点到三角形各顶点的距离相等三角形各内角角平分线的交点到三角形各边的距离相等例题1:如图,在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的
度数。 分析: ∠O = ? ∠1 + ∠3= ? O为△ABC的内心 BO是∠ABC的角平分线 CO是∠ACB的角平分线 三角形内心性质的应用解: ∵点O为△ABC的内心 ∴∠1=∠2= ∴ ∠BOC=1800 - (∠1+∠3)
=1800 - (250+37.50)
=117.50
∴ ∠BOC=117.50
C三角形内心性质的应用延伸与拓展如图,在△ABC中,∠A=n°,点I是内心,求∠BIC的度数。解:∠BIC=1800-(∠IBC+∠ICB)
=1800-=1800-=1800-900+=900+一般地: △ABC的内心为I, ∠A=n0
则∠BIC=900+例2、求等边三角形的内切圆半径r与
外接圆半径R的比。解:由等腰三角形底边上的中垂线与顶角平分线重合的性质知,等边三角形的内切圆与外接圆是两个同心圆设内切圆切BC于D,连接OB,OD于是就有sin∠OBD=sin30°=
知 识 的 应 用·BDEFOCA如图,△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.解:设△ABC的内切圆与三边相切于D、E、F,连结OA、OB、OC、OD、OE、OF,则OD⊥AB,OE⊥BC,OF⊥AC.∴S△ABC=S△AOB+S△BOC +S△AOC= AB·OD+ BC·OE+ AC·OF= l·r设△ABC的三边为a、b、c,面积为S,
则△ABC的内切圆的半径 r=结论三角形的内切圆的有关计算·ABCEDFO如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.设AD= x , BE= y ,CE= r ∵ ⊙O与Rt△ABC的三边都相切∴AD=AF,BE=BF,CE=CD解:设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OD⊥AC,OE⊥BC,OF⊥AB。结论r如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。如图:直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径为:2cm练习·ABCEDFO如图,Rt△ABC中,∠C=90°,BC=3,AC=4, ⊙O为Rt△ABC的内切圆. (1)求Rt△ABC的内切圆的半径 . (2)若移动点O的位置,使⊙O保持与△ABC的边AC、BC都相切,求⊙O的半径r的取值范围。设AD= x , BE= y ,CE= r ∵ ⊙O与Rt△ABC的三边都相切∴AD=AF,BE=BF,CE=CD解:(1)设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。解得r=1在Rt△ABC中,BC=3,AC=4, ∴AB=5由已知可得四边形ODCE为正方形,∴CD=CE=OD∴ Rt△ABC的内切圆的半径为1。(2)如图所示,设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连结OB、OD,则四边形BODC为正方形。·ABODC∴OB=BC=3∴半径r的取值范围为0<r≤3点评几何问题代数化是解决几何问题的一种重要方法。例.如图,△ABC中,∠C =90o ,它的
内切圆O分别与边AB、BC、CA相切
于点D、E、F,且BD=12,AD=8,
求⊙O的半径r.
基础题:1.既有外接圆,又内切圆的平行四边形是______.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O是边长为2cm的正方形ABCD的内切圆,EF切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.EFHG正方形22cm2cm 1、如图,四边形ABCD的边 AB,BC,CD,DA和⊙O分别相切于L,M,N,P。
(1)图中有几对相等的线段?(2)由此你能发现什么结论? 为什么?∵ AB,BC,CD,DA都与⊙O相切,L,M,N,P是切点,∴AL=AP,LB=MB,
DN=DP,NC=MC∴AL+ LB+ DN+ NC = AP+ MB+DP+MC即 AB+ CD = AD+BC圆的外切四边形的两组对边的和相等延伸与拓展2、圆内接平行四边形是矩形圆外切平行四边形是_______延伸与拓展菱形3、圆内接梯形为等腰梯形4、已知圆外切等腰梯形的中位线长
为3cm,则腰长为____3cm延伸与拓展8cm6cm4cm6cm课堂练习1、判断:
如图:1、△ABC是圆D的外切三角形。( )
2、圆D是△ABC的外接圆。 ( )
3、△ABC是圆O的外接三角形。 ( )
2、到三角形三边距离相等的点是三角形的( )
A、内心 B、外心
3、一个直角三角形的斜边的长为10cm,内切圆的半径为1cm,则三角形的周长是-------------- ABCDO检测4.已知:△ABC中,E是内心,∠A的平 分线和△ABC的外接圆相交于点D,
求证:DE=DB=DC
ABCDE补充练习4.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出锅盖的直径,请你利用图乙,说
明她这样做的道理.同学们要好好学习老师期盼你们快快进步!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
