数学九年级上青岛版3.4 直线与圆的位置关系课件6
文档属性
| 名称 | 数学九年级上青岛版3.4 直线与圆的位置关系课件6 |  | |
| 格式 | zip | ||
| 文件大小 | 830.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 07:21:33 | ||
图片预览






文档简介
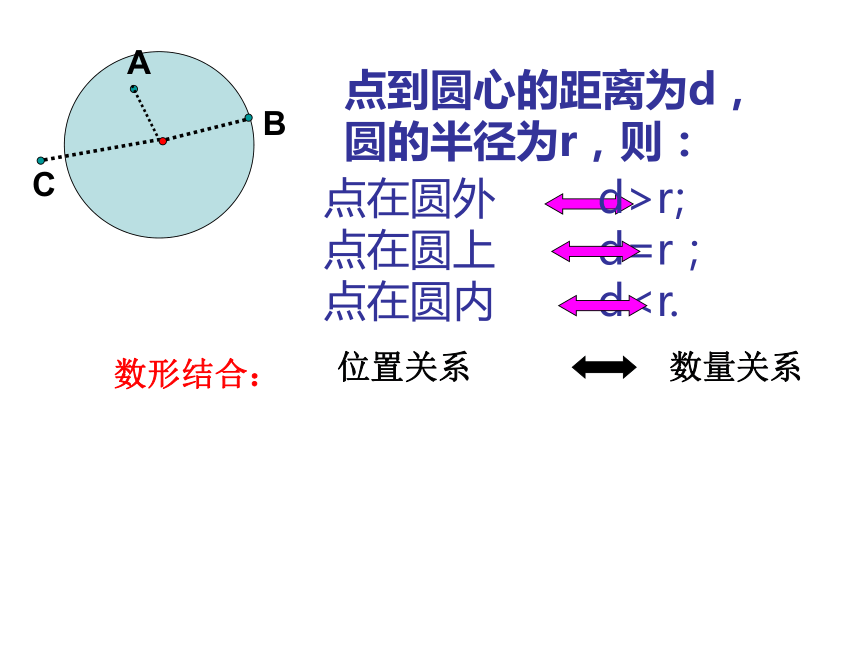
课件29张PPT。直线与圆的位置关系1、点与圆有几种位置关系??2、怎样判定点和圆的位置关系?.A.A.A.A.A . B.A.A.C.A.A(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。大于等于小于·复习回顾 点到圆心的距离为d,圆的半径为r,则:点在圆外 d>r;
点在圆上 d=r;
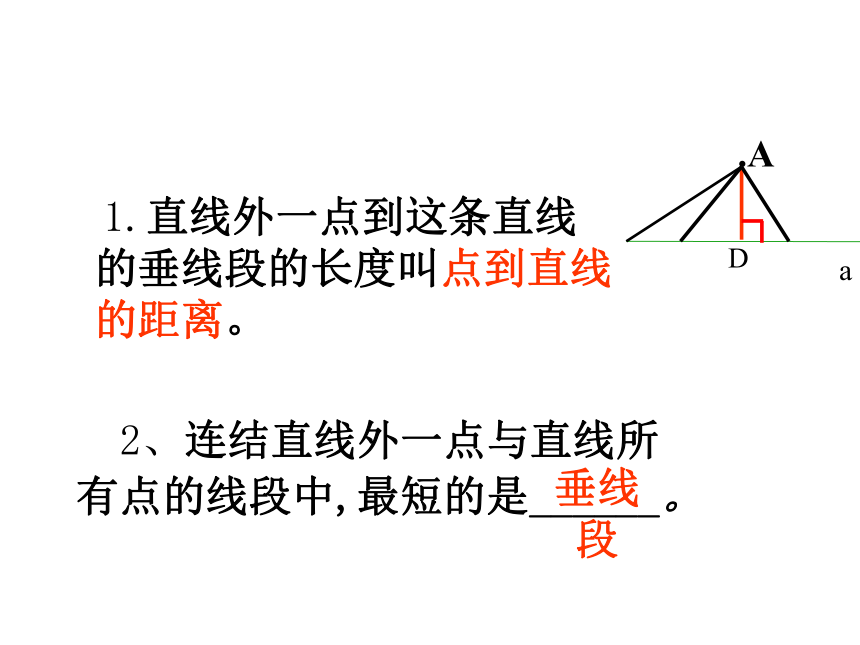
点在圆内 dABC位置关系数形结合:数量关系2、连结直线外一点与直线所
有点的线段中,最短的是______。 1.直线外一点到这条直线
的垂线段的长度叫点到直线
的距离。垂线段
a .AD同学们,在我们的生活中到处都蕴含着数学知识,下面老师请同学们欣赏美丽的
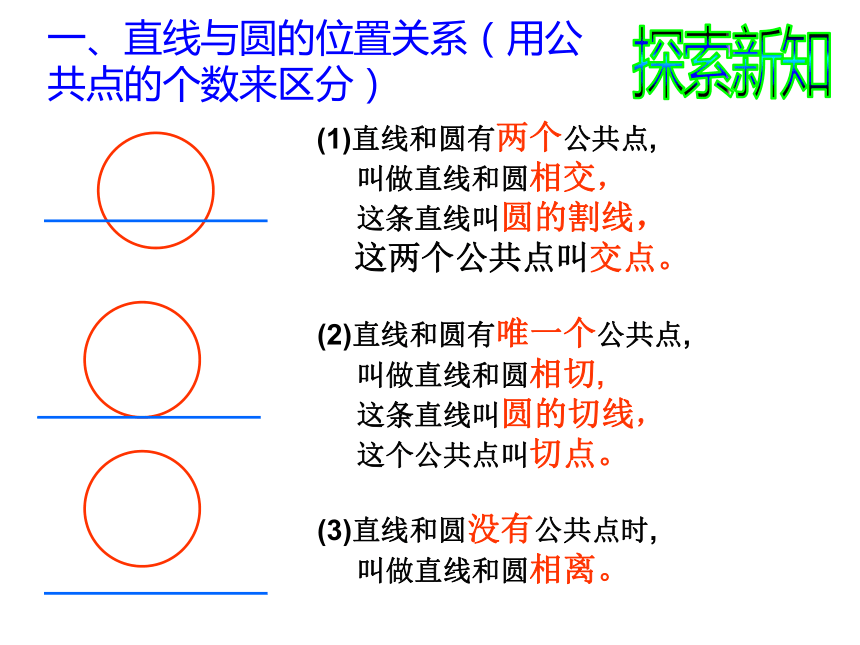
海上日出从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?今天老师和同学们一起来探究直线与圆的位置关系(一) 请同学们利用手中的工具再现海上日出的整个情景。我们可以在纸上画一个圆,把你手中的三角尺的一边当作一条直线,推动三角尺,你能发现直线与圆的公共点的个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
在再现过程中,你认为直线与圆的位置关系可以分为哪几类?
你分类的依据是什么?操作与思考(地平线)a(地平线)(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点。(1)直线和圆有两个公共点,
叫做直线和圆相交,
这条直线叫圆的割线,
这两个公共点叫交点。(3)直线和圆没有公共点时,
叫做直线和圆相离。一、直线与圆的位置关系(用公共点的个数来区分)探索新知相交相切相离上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系? 你能根据d与r的大小关系确定直线与圆的位置关系吗?直线与圆的位置关系量化揭密直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化揭密<=>位置关系数量关系数形结合总结:判定直线与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据性质,由_________________ 的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r
科学训练1、直线与圆最多有两个公共
点 。…………………( )
2、若直线与圆相交,则直线上的
点都在圆内。… … … …( )
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
√×一、判断.A.B.C.O.Om×.A.B.O二:快速判断下列各图中直线与圆的位置关系ll.O2lL.A
3、如图,在Rt△ABC中,∠C=90°,AB=5cm,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是 cm。
4、直线L 和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。12/5D例: 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm.分析:要了解AB与⊙C的位置
关系,只要知道圆心C到AB的
距离d与r的关系.已知r,只需
求出C到AB的距离d。
d解:过C作CD⊥AB,垂足为D在△ABC中,AB=5根据三角形的面积公式有∴即圆心C到AB的距离d=2.4cm所以 (1)当r=2cm时,有d>r,因此⊙C和AB相离。d(2)当r=2.4cm时,有d=r,因此⊙C和AB相切。(3)当r=3cm时,有d线段AB与⊙C只有一个公共点。
当r满足 时,
线段AB与⊙C没有公共点。
当r满足 时, 线段AB
与⊙C有两个公共点。CD= cm0≤r<2.4或r>42.4 <r ≤3相交相切相离d > 5cmd = 5cmd < 5cm小试牛刀0cm≤2101、已知:圆的直径为13cm,如果直线和 圆心的距离为以下值时,直线和圆有几个 公共点?为什么?(1) 4.5cmA 0 个; B 1个; C 2个;答案:C(2) 6.5cm答案:B(3) 8cm答案:AA 0 个; B 1个; C 2个;A 0 个; B 1个; C 2个;自我检验2、如图,已知∠BAC=30度,M为AC 上一点,且AM=5cm,以M为圆心、 r为半径的圆与直线AB有怎样的 位置关系?为什么?(1) r=2cm(2) r=4cm(3) r=2.5cmA.(-3,-4)O 已知⊙A的直径为6,点A的坐标为
(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。BC43相离相切-1-1拓展.(-3,-4)OBC43-1-1若⊙A要与x轴相切,则⊙A该向上移动多少个单位?若⊙A要与x轴相交呢?思考 已知⊙O的半径r=7cm,直线l1 // l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离m.观察小结:1、直线与圆的位置关系:0d>r1d=r切点切线2d
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。大于等于小于·复习回顾 点到圆心的距离为d,圆的半径为r,则:点在圆外 d>r;
点在圆上 d=r;
点在圆内 d
有点的线段中,最短的是______。 1.直线外一点到这条直线
的垂线段的长度叫点到直线
的距离。垂线段
a .AD同学们,在我们的生活中到处都蕴含着数学知识,下面老师请同学们欣赏美丽的
海上日出从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?今天老师和同学们一起来探究直线与圆的位置关系(一) 请同学们利用手中的工具再现海上日出的整个情景。我们可以在纸上画一个圆,把你手中的三角尺的一边当作一条直线,推动三角尺,你能发现直线与圆的公共点的个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
在再现过程中,你认为直线与圆的位置关系可以分为哪几类?
你分类的依据是什么?操作与思考(地平线)a(地平线)(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点。(1)直线和圆有两个公共点,
叫做直线和圆相交,
这条直线叫圆的割线,
这两个公共点叫交点。(3)直线和圆没有公共点时,
叫做直线和圆相离。一、直线与圆的位置关系(用公共点的个数来区分)探索新知相交相切相离上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系? 你能根据d与r的大小关系确定直线与圆的位置关系吗?直线与圆的位置关系量化揭密直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系量化揭密<=>位置关系数量关系数形结合总结:判定直线与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据性质,由_________________ 的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r
科学训练1、直线与圆最多有两个公共
点 。…………………( )
2、若直线与圆相交,则直线上的
点都在圆内。… … … …( )
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
√×一、判断.A.B.C.O.Om×.A.B.O二:快速判断下列各图中直线与圆的位置关系ll.O2lL.A
3、如图,在Rt△ABC中,∠C=90°,AB=5cm,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是 cm。
4、直线L 和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。12/5D例: 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm.分析:要了解AB与⊙C的位置
关系,只要知道圆心C到AB的
距离d与r的关系.已知r,只需
求出C到AB的距离d。
d解:过C作CD⊥AB,垂足为D在△ABC中,AB=5根据三角形的面积公式有∴即圆心C到AB的距离d=2.4cm所以 (1)当r=2cm时,有d>r,因此⊙C和AB相离。d(2)当r=2.4cm时,有d=r,因此⊙C和AB相切。(3)当r=3cm时,有d
当r满足 时,
线段AB与⊙C没有公共点。
当r满足 时, 线段AB
与⊙C有两个公共点。CD= cm0≤r<2.4或r>42.4 <r ≤3相交相切相离d > 5cmd = 5cmd < 5cm小试牛刀0cm≤2101、已知:圆的直径为13cm,如果直线和 圆心的距离为以下值时,直线和圆有几个 公共点?为什么?(1) 4.5cmA 0 个; B 1个; C 2个;答案:C(2) 6.5cm答案:B(3) 8cm答案:AA 0 个; B 1个; C 2个;A 0 个; B 1个; C 2个;自我检验2、如图,已知∠BAC=30度,M为AC 上一点,且AM=5cm,以M为圆心、 r为半径的圆与直线AB有怎样的 位置关系?为什么?(1) r=2cm(2) r=4cm(3) r=2.5cmA.(-3,-4)O 已知⊙A的直径为6,点A的坐标为
(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。BC43相离相切-1-1拓展.(-3,-4)OBC43-1-1若⊙A要与x轴相切,则⊙A该向上移动多少个单位?若⊙A要与x轴相交呢?思考 已知⊙O的半径r=7cm,直线l1 // l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离m.观察小结:1、直线与圆的位置关系:0d>r1d=r切点切线2d
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
