数学九年级上青岛版3.7正多边形与圆课件2
文档属性
| 名称 | 数学九年级上青岛版3.7正多边形与圆课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 396.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 07:25:35 | ||
图片预览





文档简介
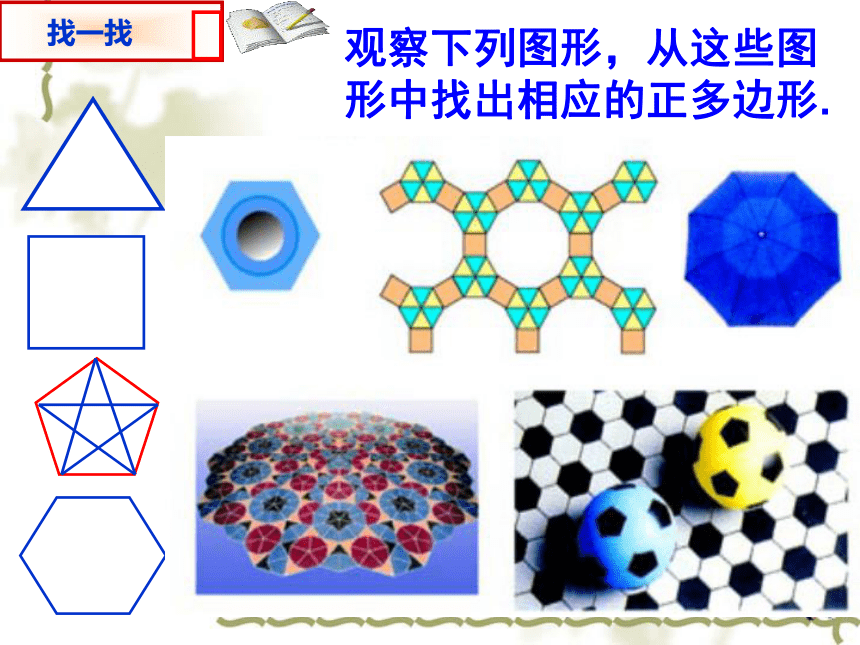
课件31张PPT。各边相等,各角也相等的多边形是正多边形.
正n 边形:如果一个正多边形有n 条边,
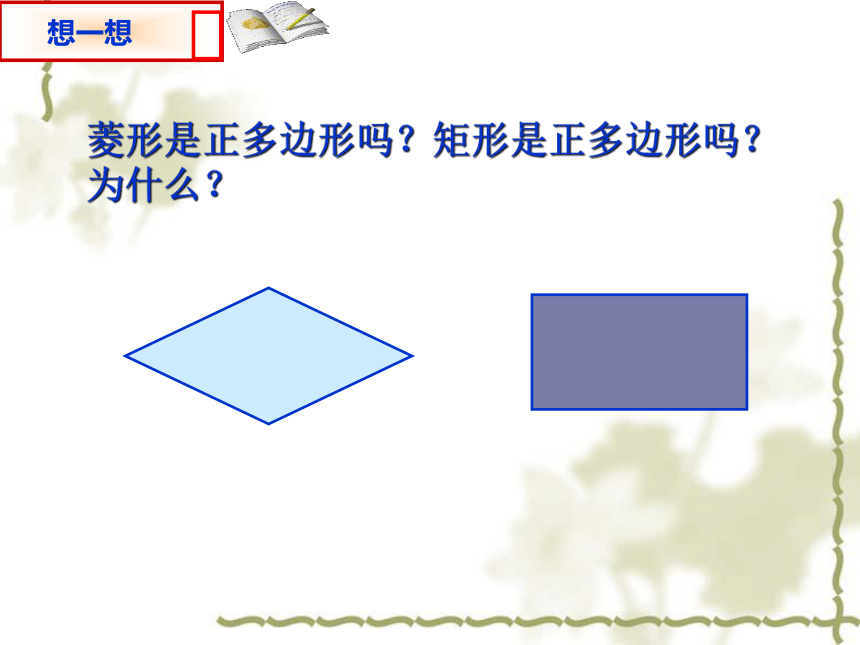
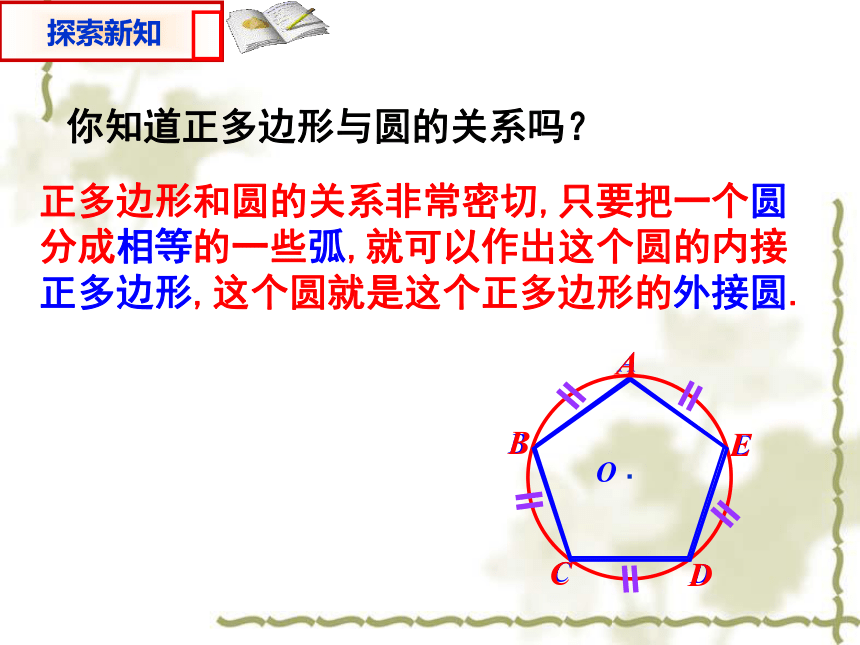
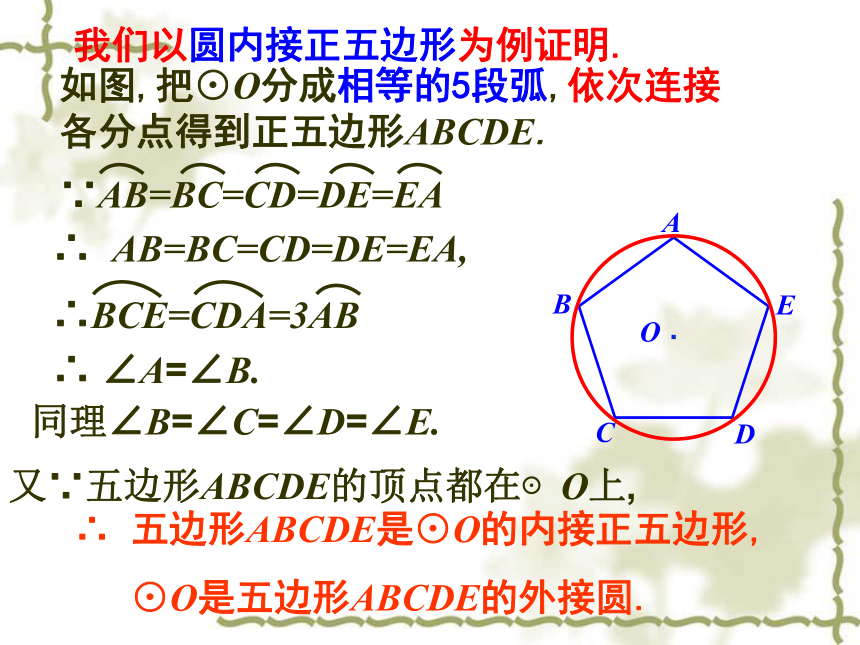
那么这个正多边形叫做正n 边形.三条边相等,三个角相等(60°)四条边相等,四个角相等(90°)正多边形定义3.7正多边形和圆 观察下列图形,从这些图形中找出相应的正多边形.菱形是正多边形吗?矩形是正多边形吗?为什么?你知道正多边形与圆的关系吗?正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.如图,把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.∴ AB=BC=CD=DE=EA,∴ ∠A=∠B.同理∠B=∠C=∠D=∠E.又∵五边形ABCDE的顶点都在⊙O上,∴ 五边形ABCDE是⊙O的内接正五边形,
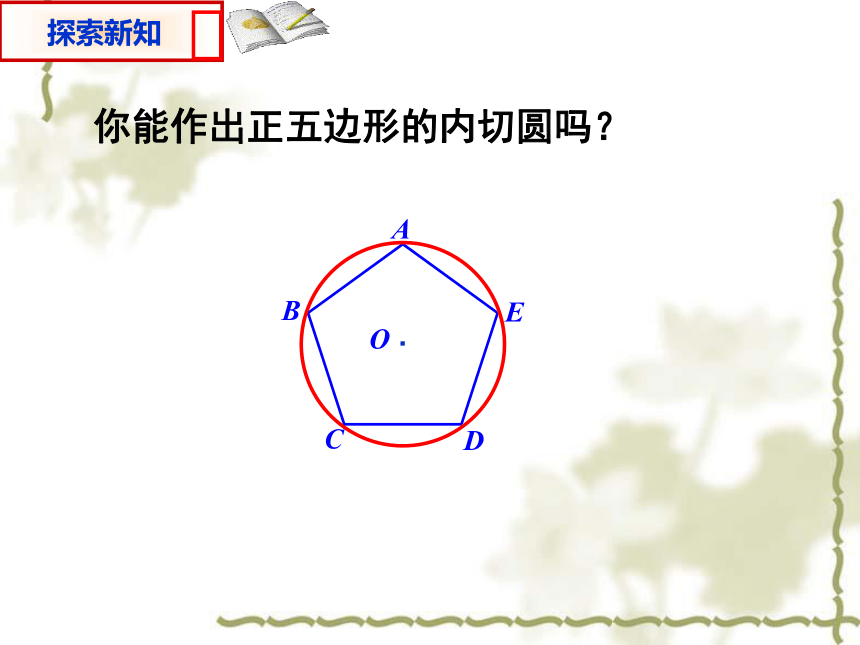
⊙O是五边形ABCDE的外接圆.我们以圆内接正五边形为例证明.你能作出正五边形的内切圆吗?③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB )①我们把一个正多边形的外接圆(内切圆)的圆心叫做这个正多边形的中心(即点O)②外接圆的半径叫做正多边形的半径(即OA)④中心到正多边形的一边的距离叫做正多边形的边心距(内切圆的半径、即OM)正n边形的每一个内角的度数都是____________;
中心角是___________;
正多边形的中心角与外角的大小关系
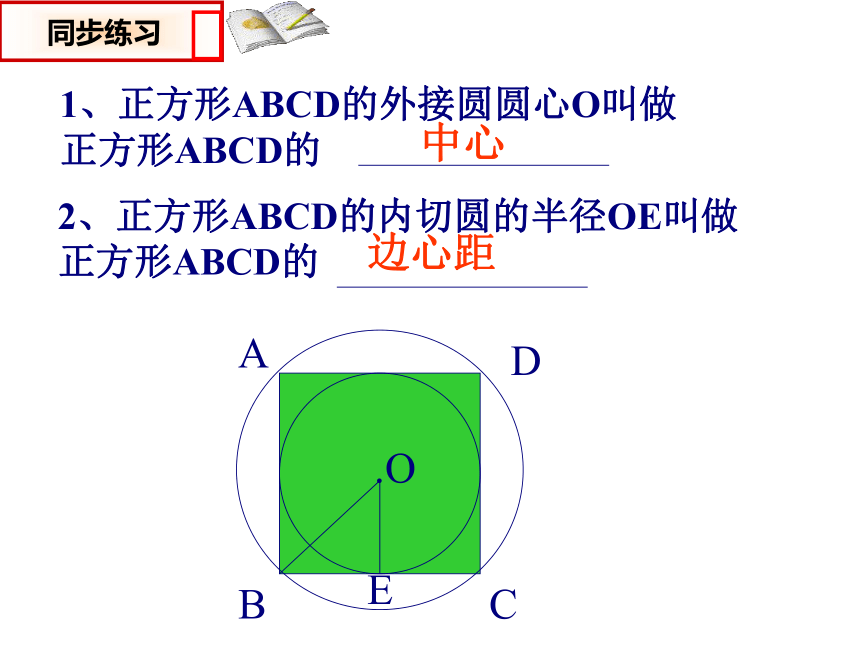
是________.相等1、正方形ABCD的外接圆圆心O叫做
正方形ABCD的2、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的ABCD.OE中心边心距3、图中正六边形ABCDEF的中心角是
它的度数是4、你发现正六边形ABCDEF的半径与边长具有
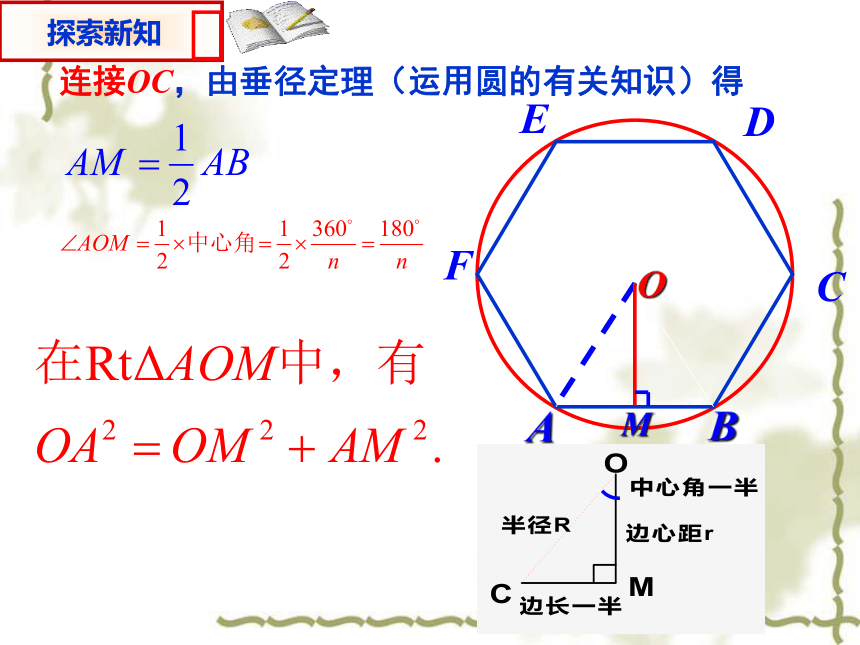
什么数量关系?为什么? BA∠AOB60度M连接OC,由垂径定理(运用圆的有关知识)得.O中心角ABG边心距OG把△AOB分成
2个全等的直角三角形设正多边形的边长为a,半径为R,它的周长为L=na.Ra例. 有一个亭子,它的地基半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.因此,亭子地基的周长l =4×6=24(m).OABCDEFRPr利用勾股定理,可得边心距亭子地基的面积在Rt△OPC中,OC=4, PC=OABCDEFRPr1.正八边形的每个内角是______度.135°2.如图,正六边形ABCDEF内接于⊙O,则∠CFD的度数是( )
A. 60° B. 45° C. 30° D. 22.5°C 3.如果一个正多边形绕它的中心旋转90°就与原来的图形重合,那么这个正多边形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形B 4.已知正六边形的边心距为 ,则它的周长是_____. 125.如图,正六边形ABCDEF的半径为2,以它的中心O为坐标原点,顶点B、E在x轴上,求正六边形ABCDEF的各顶点的坐标.A(-1, )B(-2,0 )C(-1, )D(1, )E(2,0 )F( 1, )6.如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为( )
A. 40 B .50 C. 60 D. 80 A7.边长为6的正三角形的半径是________.8.如图,⊙O的周长为 cm,求以它的半径为边长的正六边形ABCDEF的面积. 分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.解:作等边△ABC的BC边上的高AD,垂足为D连接OB,则OB=R,BC=a在Rt△OBD中 ∠OBD=30°,·ABCDO边心距=OD= BD=R即正三角形的边长为 边心距为 面积为 解:连接OB,OC 作OE⊥BC垂足为E,
∠OEB=90° ∠OBE= ∠ BOE=45°在Rt△OBE中为等腰直角三角形·ABCDOE1.课本P107第1题正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。怎样画一个正多边形呢?
问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.120 °①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
AOCB你能用以上方法画出正四边形、正五边形、正六边形吗?·ABCDOOABCDEF·90°72°60°你能尺规作出正六边形、正三角形、正十二边形吗?OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… ABCDMN1、正多边形的各边相等2、正多边形的各角相等二、正多边形的计算:一、正多边形的性质:三、画正多边形的方法1.用量角器等分圆
2.尺规作图等分圆
正n 边形:如果一个正多边形有n 条边,
那么这个正多边形叫做正n 边形.三条边相等,三个角相等(60°)四条边相等,四个角相等(90°)正多边形定义3.7正多边形和圆 观察下列图形,从这些图形中找出相应的正多边形.菱形是正多边形吗?矩形是正多边形吗?为什么?你知道正多边形与圆的关系吗?正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.如图,把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.∴ AB=BC=CD=DE=EA,∴ ∠A=∠B.同理∠B=∠C=∠D=∠E.又∵五边形ABCDE的顶点都在⊙O上,∴ 五边形ABCDE是⊙O的内接正五边形,
⊙O是五边形ABCDE的外接圆.我们以圆内接正五边形为例证明.你能作出正五边形的内切圆吗?③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB )①我们把一个正多边形的外接圆(内切圆)的圆心叫做这个正多边形的中心(即点O)②外接圆的半径叫做正多边形的半径(即OA)④中心到正多边形的一边的距离叫做正多边形的边心距(内切圆的半径、即OM)正n边形的每一个内角的度数都是____________;
中心角是___________;
正多边形的中心角与外角的大小关系
是________.相等1、正方形ABCD的外接圆圆心O叫做
正方形ABCD的2、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的ABCD.OE中心边心距3、图中正六边形ABCDEF的中心角是
它的度数是4、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么? BA∠AOB60度M连接OC,由垂径定理(运用圆的有关知识)得.O中心角ABG边心距OG把△AOB分成
2个全等的直角三角形设正多边形的边长为a,半径为R,它的周长为L=na.Ra例. 有一个亭子,它的地基半径为4 m的正六边形,求地基的周长和面积(精确到0.1 m2).解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.因此,亭子地基的周长l =4×6=24(m).OABCDEFRPr利用勾股定理,可得边心距亭子地基的面积在Rt△OPC中,OC=4, PC=OABCDEFRPr1.正八边形的每个内角是______度.135°2.如图,正六边形ABCDEF内接于⊙O,则∠CFD的度数是( )
A. 60° B. 45° C. 30° D. 22.5°C 3.如果一个正多边形绕它的中心旋转90°就与原来的图形重合,那么这个正多边形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形B 4.已知正六边形的边心距为 ,则它的周长是_____. 125.如图,正六边形ABCDEF的半径为2,以它的中心O为坐标原点,顶点B、E在x轴上,求正六边形ABCDEF的各顶点的坐标.A(-1, )B(-2,0 )C(-1, )D(1, )E(2,0 )F( 1, )6.如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为( )
A. 40 B .50 C. 60 D. 80 A7.边长为6的正三角形的半径是________.8.如图,⊙O的周长为 cm,求以它的半径为边长的正六边形ABCDEF的面积. 分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.解:作等边△ABC的BC边上的高AD,垂足为D连接OB,则OB=R,BC=a在Rt△OBD中 ∠OBD=30°,·ABCDO边心距=OD= BD=R即正三角形的边长为 边心距为 面积为 解:连接OB,OC 作OE⊥BC垂足为E,
∠OEB=90° ∠OBE= ∠ BOE=45°在Rt△OBE中为等腰直角三角形·ABCDOE1.课本P107第1题正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心。边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。怎样画一个正多边形呢?
问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.120 °①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
AOCB你能用以上方法画出正四边形、正五边形、正六边形吗?·ABCDOOABCDEF·90°72°60°你能尺规作出正六边形、正三角形、正十二边形吗?OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… ABCDMN1、正多边形的各边相等2、正多边形的各角相等二、正多边形的计算:一、正多边形的性质:三、画正多边形的方法1.用量角器等分圆
2.尺规作图等分圆
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
