数学九年级上青岛版3对圆的进一步认识复习课件3
文档属性
| 名称 | 数学九年级上青岛版3对圆的进一步认识复习课件3 |  | |
| 格式 | zip | ||
| 文件大小 | 659.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 07:27:03 | ||
图片预览





文档简介
课件39张PPT。第3章 对圆的进一步认识(复习课)新青岛版数学九年级上册1、了解圆的有关概念,探索并理解垂径定理,探索并认识圆心角、弧、弦之间的相等关系的定理,探索并理解圆周角和圆心角的关系定理.
2、探索并理解点和圆、直线与圆以及圆与圆的位置关系:了解切线的概念,探索切线与过切点的直径之间的关系,能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.
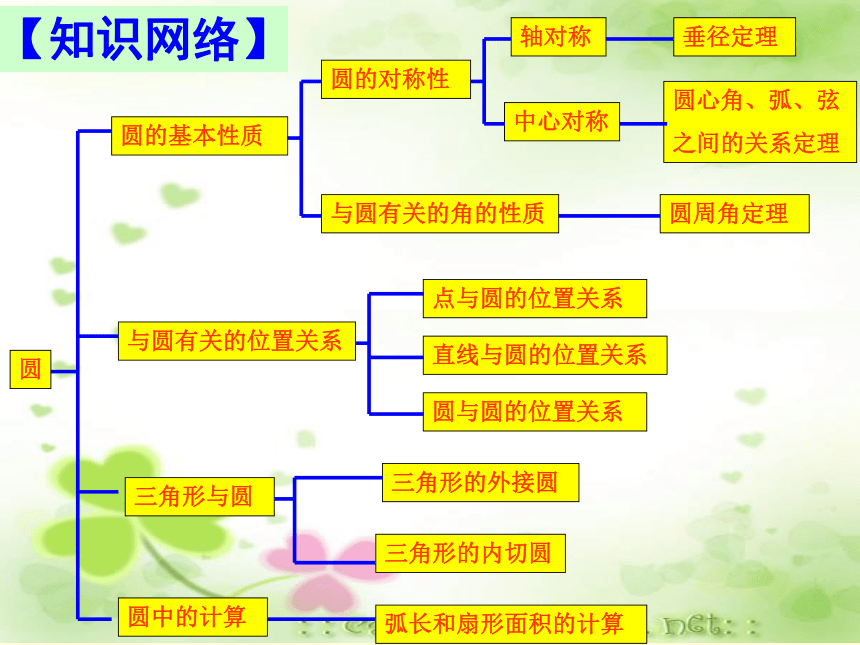
3、熟练掌握弧长和扇形面积公式及其它们的应用;理解圆锥的侧面展开图并熟练掌握圆锥的侧面积和全面积的计算.【学习目标】【重难点】1、垂径定理; 2、与圆有关的位置关系;3、弧长公式和扇形面积公式的应用.1、垂径定理; 2、切线的性质与判定.重点 难点 【知识网络】【教学内容】知识点一:圆的有关概念1、圆的定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,
另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径.
2、弦、直径、弧的概念
(1)弦:连接圆上任意两点的线段叫做弦.
(2)直径:经过圆心的弦叫做直径。直径等于半径的2倍.
(3)弧:圆上任意两点间的部分叫做圆弧,简称弧.
大于半圆的弧叫做优弧(多用三个字母表示);
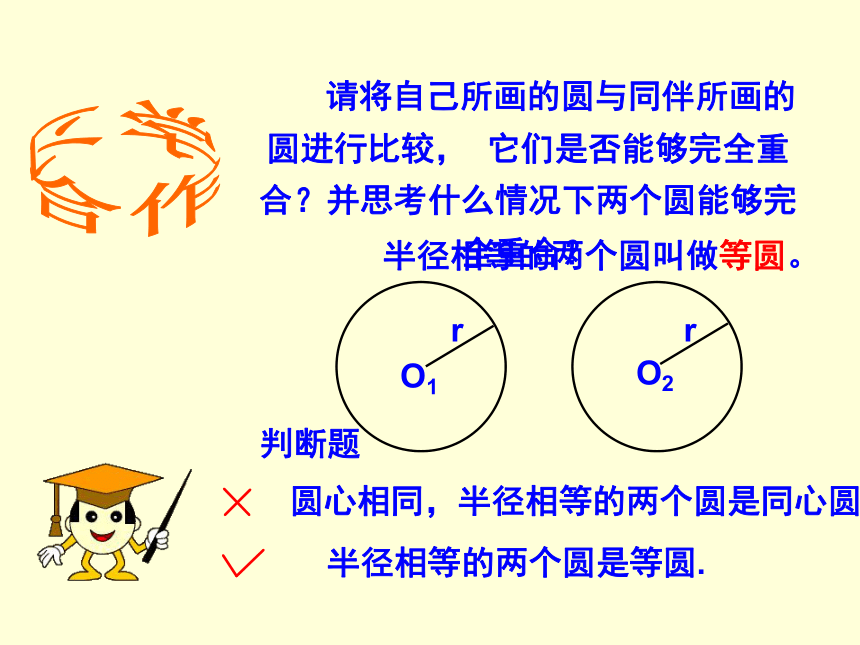
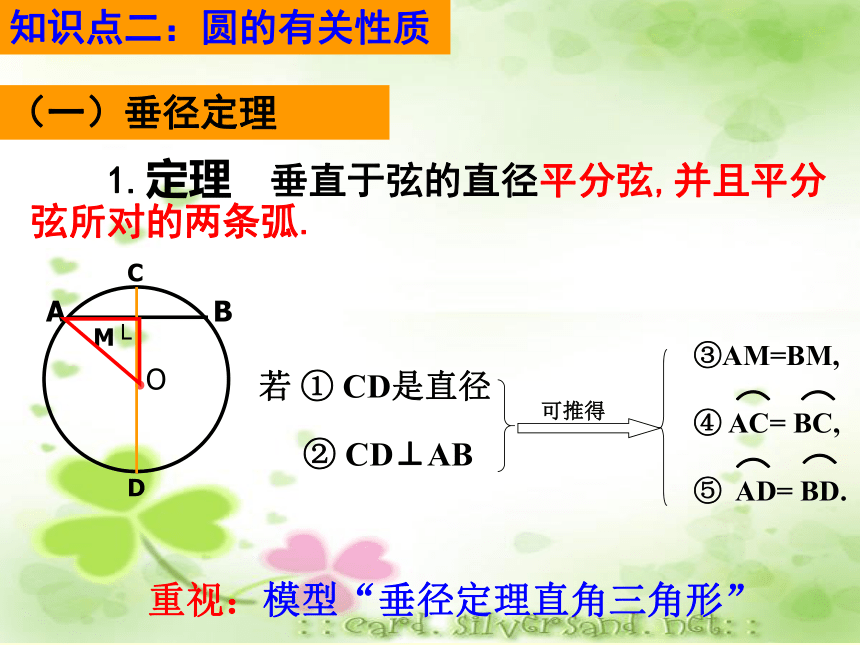
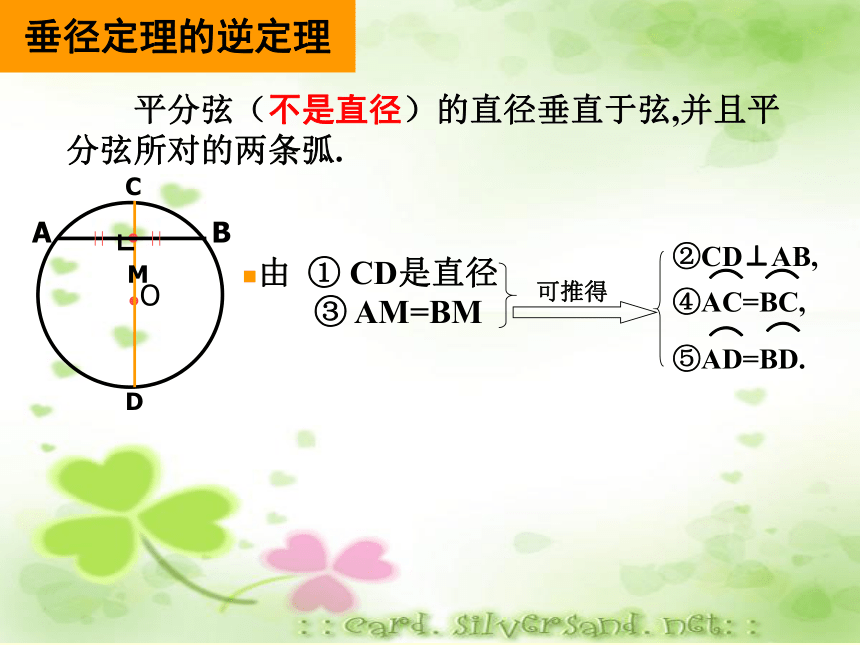
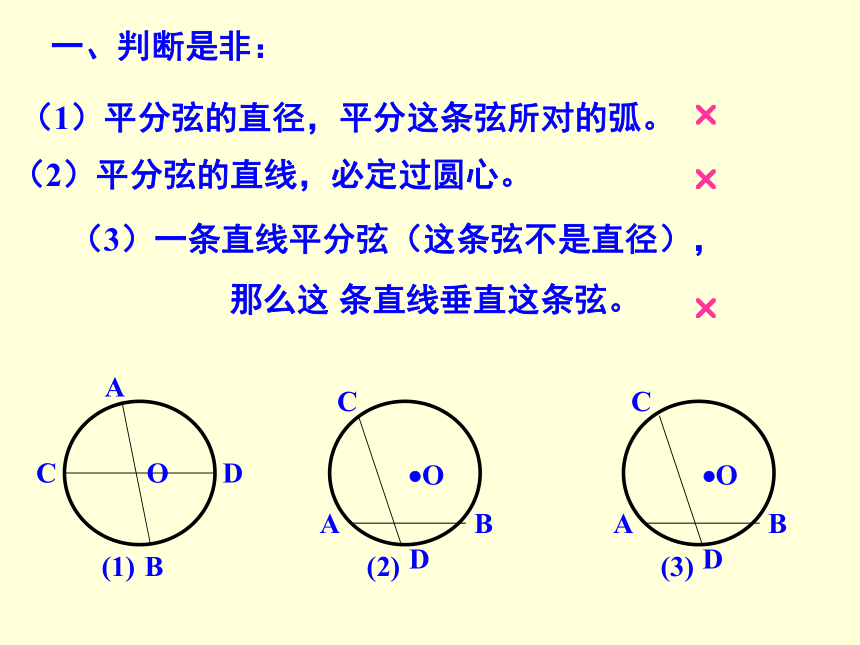
小于半圆的弧叫做劣弧(多用两个字母表示).想一想判断下列说法的正误:(1)弦是直径;(2)半圆是弧;(3)过圆心的线段是直径;(4)过圆心的直线是直径;(5)半圆是最长的弧;(6)直径是最长的弦;(7)等弧就是拉直以后长度相等的弧 合作学习 请将自己所画的圆与同伴所画的圆进行比较, 它们是否能够完全重合?并思考什么情况下两个圆能够完全重合?半径相等的两个圆叫做等圆。 圆心相同,半径相等的两个圆是同心圆; 半径相等的两个圆是等圆.判断题(一)垂径定理③AM=BM,重视:模型“垂径定理直角三角形” 若 ① CD是直径② CD⊥AB 1.定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.知识点二:圆的有关性质垂径定理的逆定理 平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.一、判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),
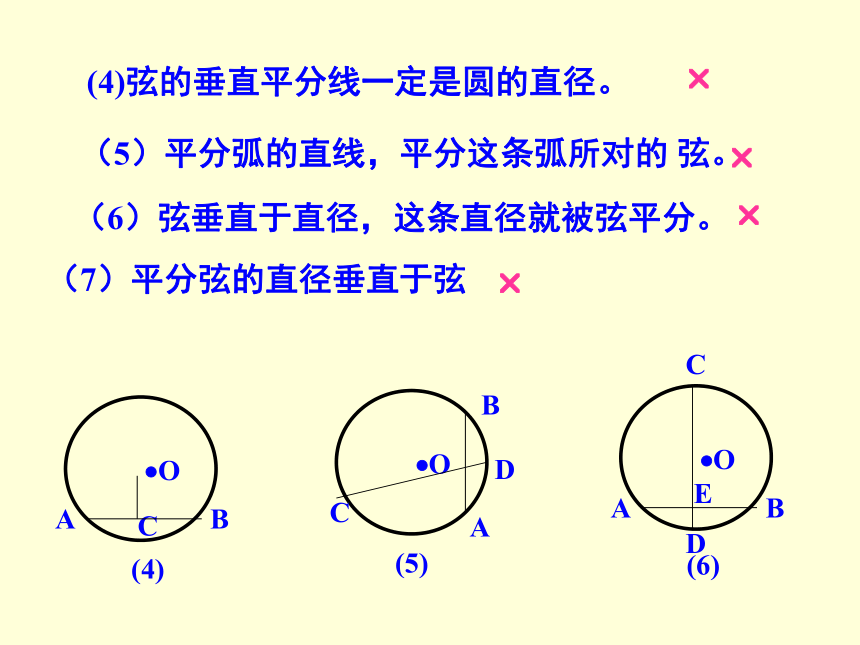
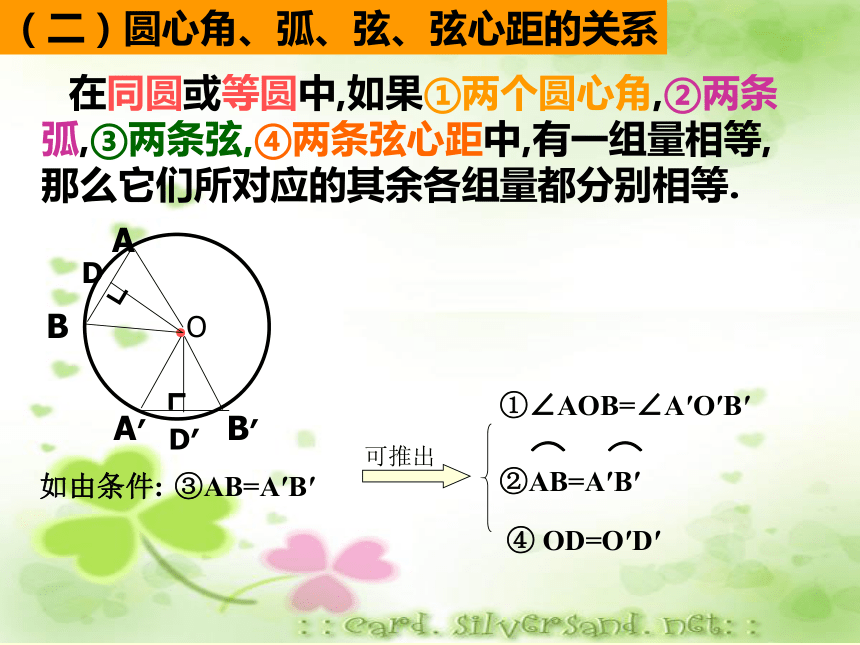
那么这 条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。???(7)平分弦的直径垂直于弦? 在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′(二)圆心角、弧、弦、弦心距的关系(三)圆周角定理及推论 90°的圆周角所对的弦是 . 定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半. 推论:直径所对的圆周角是 .直角直径知识点三:与圆有关的位置关系 (一)点与圆的位置关系 设⊙O的半径为r,点P到圆心的距离为d,
则有:点P在圆外d>r
点P在圆上d=r
点P在圆内dr切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.CD●OA 如图
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线. 经过圆外一点的切线,这点和切点之间的线段的长,叫做这个点到圆的切线长 从圆一点外可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。切线长定理:从一块三角形材料中,能否剪下一个圆,使其与各边都相切?老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.三角形与圆的位置关系I●I●切线的性质定理圆的切线垂直于过切点的半径.
∵CD切⊙O于A, OA是⊙O的半径CD●OA ∴CD⊥OA.知识点四:圆中的计算问题弧长公式扇形面积公式知识精华:2.半径:正多边形外接圆的半径叫做这个正多边形的半径.1.中心:一个正多边形外接圆的圆心叫做这个正多边形的中心.O3.中心角:正多边形每以边所对的外接圆的圆心角叫做这个正多边形的中心角.4.边心距:中心到正多边形一边的距离叫做这个正多边形的边心距.一、知识要点概述 1、弧长公式和扇形面积公式 n°的圆心角所对的弧长l和含n°圆心角的扇形的面积公式不要死记硬背,可依比例关系很快地随手推来: 这样就不至于因死记硬背而出错. 将弧长公式代入扇形面积公式中,立即得到用弧长和半径表示的扇形面积公式: 这一公式与三角形面积公式酷似.为了便于记忆,只要把扇形看成一个曲边三角形,把弧长l看成底、R看成底边上的高即可.2、弓形面积 弓形面积可以看作是扇形面积和三角形面积的分解与组合,实际应用时,可根据图形直观选用下列公式: ①当弓形所含的弧是劣弧时,如图(甲), S弓形=S扇形OAB-S△AOB; ②当弓形所含的弧是优弧时,如图(乙), ③当弓形所含的弧是半圆时,如图(丙),三、典型例题赏析 例1、如图,△ABC是正三角形.曲线CDEF…叫做正三角形的渐开线,其中 …的圆心依次按A、B、C循环,它们依次相连结.如果AB=1,那么曲线CDEF的长是多少? 例1、如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若BC=3cm,
sinP=0.6,求⊙O的直径.3方法总结:由AB为⊙O的直径,AB⊥CD得弧BC等于弧BD,从而得∠P=∠A,并连接AC构造Rt△ABC是解题的关键.
【典例解析】例2、如图,AB为⊙O的直径,BC与⊙O相切于B,AC交⊙O于E,点D是BC边的中点,连结DE.
(1)求证:DE与⊙O相切;
(2)若⊙O的半径为 , ,求AE.
6方法总结:
1、如果已知直线与圆有交点,常连接圆心与交点,再证明连线垂直于半径即可;
2、如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.方法总结:充分利用“垂径定理”与“等弧或同弧所对的圆周角相等”得出结论.1、如图,AB是⊙O的直径,AB⊥CD于点E,则在不添加辅助线的情况下,求出图中与∠CDB相等的角.【巩固练习】∠CAB∠BAD∠BCD2、如图所示,草地上一根长5米的绳子,一端拴在墙角的木桩上,另一端拴着一只小羊,那么,小羊在草地上的最大活动区域的面积是多少?1米1米 方法总结:正确画出小羊的最大活动区域是解决问题的关键.
3、已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.求证:DE是⊙O的切线.解题关键:
证明OD∥AC.
方法一:利用等边对等角证∠C=∠BDO;
方法二:利用三线合一证明OD为△ABC的中位线.【点击中考】 1、(2013年泰安中考)如图,点A、B、C在⊙O上,∠ABO=32°,∠ACO=38°,
则∠BOC等于( ).
(A)60 (B)70 (C)120°(D)140°D方法总结:连结OA,求出与∠BOC同弧的圆周角.2、(2013年泰安中考)如图,已知AB是⊙O的直径,AD切⊙O于点A,点E是 的中点,则下列结论不成立的是( ).
(A)OC∥AE (B)EC=BC
(C)∠DAE=∠ABE (D)AC⊥OED提示:注意垂径定理与切线的性质应用.1、如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( ).
8 B. 5 C. 10 D. 2
2、如图,∠AOB=100°,点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为( ).
A.50° B.50°或80° C.130° D.50°或130°BD【布置作业】4、如图,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是 .
50°5、如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点。若两圆的半径分别为3cm和5cm,则AB的长为______cm.86、如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若,求弦MN的长.E3X2X5教师寄语:努力就有收获!祝你们成功!
2、探索并理解点和圆、直线与圆以及圆与圆的位置关系:了解切线的概念,探索切线与过切点的直径之间的关系,能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.
3、熟练掌握弧长和扇形面积公式及其它们的应用;理解圆锥的侧面展开图并熟练掌握圆锥的侧面积和全面积的计算.【学习目标】【重难点】1、垂径定理; 2、与圆有关的位置关系;3、弧长公式和扇形面积公式的应用.1、垂径定理; 2、切线的性质与判定.重点 难点 【知识网络】【教学内容】知识点一:圆的有关概念1、圆的定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,
另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径.
2、弦、直径、弧的概念
(1)弦:连接圆上任意两点的线段叫做弦.
(2)直径:经过圆心的弦叫做直径。直径等于半径的2倍.
(3)弧:圆上任意两点间的部分叫做圆弧,简称弧.
大于半圆的弧叫做优弧(多用三个字母表示);
小于半圆的弧叫做劣弧(多用两个字母表示).想一想判断下列说法的正误:(1)弦是直径;(2)半圆是弧;(3)过圆心的线段是直径;(4)过圆心的直线是直径;(5)半圆是最长的弧;(6)直径是最长的弦;(7)等弧就是拉直以后长度相等的弧 合作学习 请将自己所画的圆与同伴所画的圆进行比较, 它们是否能够完全重合?并思考什么情况下两个圆能够完全重合?半径相等的两个圆叫做等圆。 圆心相同,半径相等的两个圆是同心圆; 半径相等的两个圆是等圆.判断题(一)垂径定理③AM=BM,重视:模型“垂径定理直角三角形” 若 ① CD是直径② CD⊥AB 1.定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.知识点二:圆的有关性质垂径定理的逆定理 平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.一、判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。???(7)平分弦的直径垂直于弦? 在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′(二)圆心角、弧、弦、弦心距的关系(三)圆周角定理及推论 90°的圆周角所对的弦是 . 定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半. 推论:直径所对的圆周角是 .直角直径知识点三:与圆有关的位置关系 (一)点与圆的位置关系 设⊙O的半径为r,点P到圆心的距离为d,
则有:点P在圆外d>r
点P在圆上d=r
点P在圆内d
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线. 经过圆外一点的切线,这点和切点之间的线段的长,叫做这个点到圆的切线长 从圆一点外可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。切线长定理:从一块三角形材料中,能否剪下一个圆,使其与各边都相切?老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.三角形与圆的位置关系I●I●切线的性质定理圆的切线垂直于过切点的半径.
∵CD切⊙O于A, OA是⊙O的半径CD●OA ∴CD⊥OA.知识点四:圆中的计算问题弧长公式扇形面积公式知识精华:2.半径:正多边形外接圆的半径叫做这个正多边形的半径.1.中心:一个正多边形外接圆的圆心叫做这个正多边形的中心.O3.中心角:正多边形每以边所对的外接圆的圆心角叫做这个正多边形的中心角.4.边心距:中心到正多边形一边的距离叫做这个正多边形的边心距.一、知识要点概述 1、弧长公式和扇形面积公式 n°的圆心角所对的弧长l和含n°圆心角的扇形的面积公式不要死记硬背,可依比例关系很快地随手推来: 这样就不至于因死记硬背而出错. 将弧长公式代入扇形面积公式中,立即得到用弧长和半径表示的扇形面积公式: 这一公式与三角形面积公式酷似.为了便于记忆,只要把扇形看成一个曲边三角形,把弧长l看成底、R看成底边上的高即可.2、弓形面积 弓形面积可以看作是扇形面积和三角形面积的分解与组合,实际应用时,可根据图形直观选用下列公式: ①当弓形所含的弧是劣弧时,如图(甲), S弓形=S扇形OAB-S△AOB; ②当弓形所含的弧是优弧时,如图(乙), ③当弓形所含的弧是半圆时,如图(丙),三、典型例题赏析 例1、如图,△ABC是正三角形.曲线CDEF…叫做正三角形的渐开线,其中 …的圆心依次按A、B、C循环,它们依次相连结.如果AB=1,那么曲线CDEF的长是多少? 例1、如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若BC=3cm,
sinP=0.6,求⊙O的直径.3方法总结:由AB为⊙O的直径,AB⊥CD得弧BC等于弧BD,从而得∠P=∠A,并连接AC构造Rt△ABC是解题的关键.
【典例解析】例2、如图,AB为⊙O的直径,BC与⊙O相切于B,AC交⊙O于E,点D是BC边的中点,连结DE.
(1)求证:DE与⊙O相切;
(2)若⊙O的半径为 , ,求AE.
6方法总结:
1、如果已知直线与圆有交点,常连接圆心与交点,再证明连线垂直于半径即可;
2、如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.方法总结:充分利用“垂径定理”与“等弧或同弧所对的圆周角相等”得出结论.1、如图,AB是⊙O的直径,AB⊥CD于点E,则在不添加辅助线的情况下,求出图中与∠CDB相等的角.【巩固练习】∠CAB∠BAD∠BCD2、如图所示,草地上一根长5米的绳子,一端拴在墙角的木桩上,另一端拴着一只小羊,那么,小羊在草地上的最大活动区域的面积是多少?1米1米 方法总结:正确画出小羊的最大活动区域是解决问题的关键.
3、已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.求证:DE是⊙O的切线.解题关键:
证明OD∥AC.
方法一:利用等边对等角证∠C=∠BDO;
方法二:利用三线合一证明OD为△ABC的中位线.【点击中考】 1、(2013年泰安中考)如图,点A、B、C在⊙O上,∠ABO=32°,∠ACO=38°,
则∠BOC等于( ).
(A)60 (B)70 (C)120°(D)140°D方法总结:连结OA,求出与∠BOC同弧的圆周角.2、(2013年泰安中考)如图,已知AB是⊙O的直径,AD切⊙O于点A,点E是 的中点,则下列结论不成立的是( ).
(A)OC∥AE (B)EC=BC
(C)∠DAE=∠ABE (D)AC⊥OED提示:注意垂径定理与切线的性质应用.1、如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( ).
8 B. 5 C. 10 D. 2
2、如图,∠AOB=100°,点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为( ).
A.50° B.50°或80° C.130° D.50°或130°BD【布置作业】4、如图,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是 .
50°5、如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,C为切点。若两圆的半径分别为3cm和5cm,则AB的长为______cm.86、如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若,求弦MN的长.E3X2X5教师寄语:努力就有收获!祝你们成功!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
