数学九年级上青岛版4.5一元二次方程的应用课件7
文档属性
| 名称 | 数学九年级上青岛版4.5一元二次方程的应用课件7 |

|
|
| 格式 | zip | ||
| 文件大小 | 591.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 00:00:00 | ||
图片预览










文档简介
课件45张PPT。4.5一元二次方程的应用 (1)审:是指读懂题目,弄清题意,明确哪些是已知量,哪些是未知量以及题目要求什么;(3)设:是指设元,也就是设未知数;(4)列:就是列方程,根据等量关系式列代数式表示相等关系中的各个量,就得到含有未知数的等式,即方程;列方程解应用题的步骤?(2)找:找等量关系式,即题目中给出的能够表达应用题全部含义的一个相等关系;(5)解:就是解方程,求出未知数的值;
(6)检验:列方程解应用题时,要对所求出的未知数进行检验,检验的目的有两个:其一,检验求出来的未知数的值是否满足方程;其二,检验求出的未知数的值是不是满足实际问题的要求,对于适合方程而不适合实际问题的未知数的值应舍去;
(7)答:就是写出答案,其中在书写时还要注意不要漏写单位名称.当x=10时, =12.5; 当x=25时, =5.均合题意 例1、如图,有一矩形空地,一边靠墙,这堵墙的长为30m,另三
边由一段长为35m的铁丝网围成.已知矩形空地的面积是125m2,
求矩形空地的长和宽.分析:根据长方形面积公式,运用长×宽=125列出方程,即可求
得答案.在方程中墙壁的长度30m没有直接用到,但在检验结果
的时候,要注意矩形的平行于墙壁的一边长不能超过30m,否则,
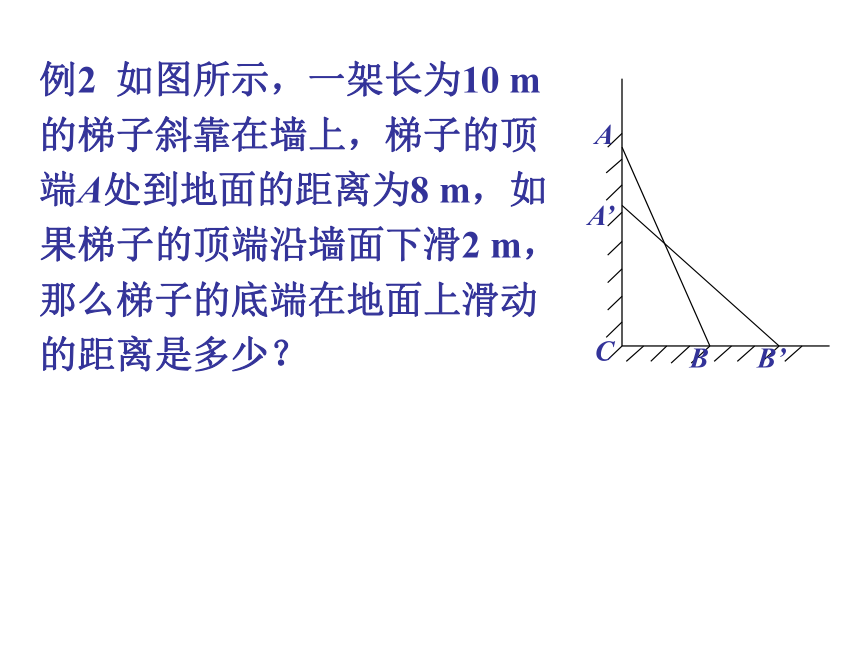
这堵墙就没有作为养鸡场的利用价值。根据题意,得 解:设矩形与墙平行的一边长为xm,则矩形的另一条边长为 m.整理,得x2-35x+250=O.答:矩形空地的长和宽分别是12.5m和10m或25m和5m解这个方程,得x1=10,x2=25. (一)几何中面积、长度问题例2 如图所示,一架长为10 m的梯子斜靠在墙上,梯子的顶端A处到地面的距离为8 m,如果梯子的顶端沿墙面下滑2 m,那么梯子的底端在地面上滑动的距离是多少? 分析:如图所示,此题的相等关系是矩形面积减去道路面积等于540m2.小结
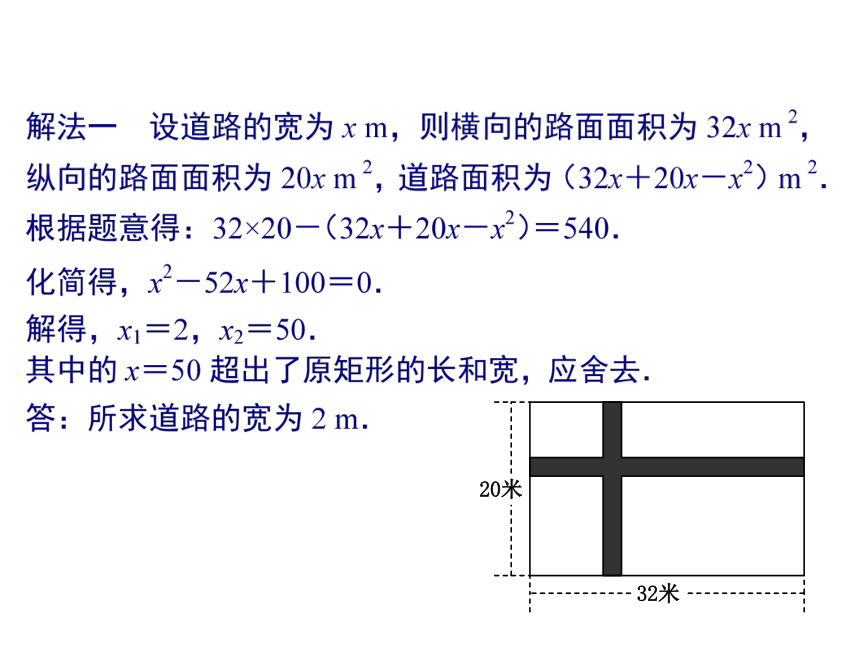
1.解法二和解法一相比更简单,它利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,可以使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路).2.有些同学在列方程解应用题时,往往看到正解就保留,看到负解就舍去.其实,即使是正解也要根据题设条件进行检验,该舍就舍.此题一定要注意原矩形“宽为20 m、长为32 m”这个条件,从而进行正确取舍.总结解决此类问题 必须具备良好的几何概念知识,熟悉长度,面积,体积等公式。
有时需要通过平移的方法来解决问题。
常见问题:挖沟的宽度,制作盒子。1、用20cm长的铁丝能否折成面积为30cm2的矩形,若能够,求它的长与宽;若不能,请说明理由.练习:解:设这个矩形的长为xcm,则宽为 cm,即x2-10x+30=0这里a=1,b=-10,c=30,∴此方程无解.∴用20cm长的铁丝不能折成面积为30cm2的矩形.练习:1.如图,用长为18m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.要围成苗圃的面积为81m2,应该怎么设计?解:设苗圃的一边长为xm,则化简得,答:应围成一个边长为9米的正方形.(二)数字与方程1. 一个两位数,它的十位数字比个位数字小3,而它的个位数字的平方恰好等于这个两位数.求这个两位数.2.有一个两位数,它的十位数字与个位数字的和是5.把这个两位数的十位数字与个位数字互换后得到另一个两位数,两个两位数的积为736.求原来的两位数.例1:平阳按“九五”国民经济发展规划要求,2003年的社会总产值要比2001年增长21%,求平均每年增长的百分率.(提示:基数为2001年的社会总产值,可视为a)设每年增长率为x,2001年的总产值为a,则2001年
a2002年
a(1+x)2003年
a(1+x) 2a(1+x) 2 =a+21%a分析:(三)增长率问题a (1+x) 2 =1.21 a
(1+x) 2 =1.21
1+x =1.1
x =0.1解:设每年增长率为x,2001年的总产值为a,则a(1+x) 2 =a+21%a答:平均每年增长的百分率为10% .例2 . 某市为了解决市民看病难的问题,决定下调药品的价格.某种药品经过连续两次降价后,由每盒200元下调至128元,求这种药品平均每次降价的百分率是多少?总结1.平均增长率问题中的基本数量关系为
A(1+X)n=B(A为始量,B为终止量,n为增长的次数,x为平均增长率)
类似的还有平均降低率问题中的基本数量关系为A(1-X)n=B(A为始量,B为终止量,n为降低的次数,x为平均降低率)
2.对于“增长率”问题,如人口的减少、利率的降低、汽车的折旧等等,都是在原来基数上减少,不能与一般性的增加和减少相混淆.练习:1.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程
为 .B4(四)储蓄问题例1.王老师把500元钱按一年定期存入银行,到期后,取出了300元捐给了灾区,剩下的200元和应得的利息又全部按一年定期存入,由于利息下调,第二次存款的年利率是第一次存款年利率的 ,这样到期后可得利息15元,求第一次存款的年利率 解:第一次存款的年利率为x,根据题意,可得方程: 整理,得20x2+8x-1=0. 解得x1=0.1=10%,x2=-0.5(舍去).因此第一次存款的年利率是10%例1. 某商场销售一批名牌衬衫,平均每天可销售出20件,每件盈利40元,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.若商场平均每天要盈利1200元,每件衬衫应降价多少元?(五)销售问题分析:这类销售问题,涉及的数量关系比较多,我们可以通过列表的方式来分析其中的数量关系.204080020+2x 40-x 1200例2 (2010南京)某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一性清仓,清仓时单价为40元.设第二个月单价降低x元.(1)填表(不需化简):(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?分析:800-200-(200+10x) 80-x 200+10x1. 某汽车在公路上行驶,它的路程s(m)和时间t(s)之间的关系为:s=10t+3t2,那么行驶 200m需要多长时间?(六)运动与方程例1 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发,几秒后⊿ PBQ的面积等于8cm2?解:设x秒后⊿ PBQ的面积等于8cm2
根据题意,得
整理,得
解这个方程,得所以2秒或4秒后⊿ PBQ的面积等于8cm2例2:等腰直角⊿ ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2?例1 有一根长为120 cm的绳子.
(1)能否围成一个面积是500 cm2的矩形?
(2)能否围成一个面积是1000 cm2的矩形?(八)假设存在问题分析:在解决这一类存在问题时,一般先假设
面积是500 cm2和1000 cm2的矩形存在,再根据题意列出方程求解.如果方程有解,就说明符合条件的矩形存在;如果方程无解,则说明符合条件的矩形不存在.小结例: 在一次聚会中,每两个参加聚会的人都相互握了一次手,一共握了45次手,问参加这次聚会的人数是多少?(九)统计问题分析:对这个问题,我们可以作这样的假设:如果有x个人参加聚会,那么第1个人需要与除他自己以外的其他(x-1)个人握手,要握(x-1)次手;第2个人也分别与其他(x-1)个人握手,可握(x-1)次手;……;依此类推,第x个人同样要与其他(x-1)个人握手,可握(x-1)次手,如此共有x(x-1)次握手,显然此时每两人之间都按握了两次手进行计算的.所以,按照题意,可得2(1)x(x-1)=45次手.
练习
某旅行团结束旅行,其中建议大家互相告别,细心的小明发现,每两个参加旅行的人相互握手一次,共握手66次,问这次旅行的人有多少?1.列方程解实际问题,一般分为审题、找等量关系式、设未知数、列方程、解方程、检验、写出答案这六步进行,其中审题过程虽在草稿纸上进行,但这一步非常重要,只有经过认真审题,分清已知条件和所求量,明确量与量之间的数量关系,才能准确找出相等关系,列出方程.?【方法总结】2.在列一元二次方程解实际问题时还要注意一些关键的词语,如“多”、“倍”、“差”、“提前”、“同时”、“早到”、“迟到”、“增加几倍”等. 3.在解决复杂问题时,我们可以借助于列表格等辅助方式弄清题目中的数量关系,列出方程.4.一元二次方程是我们日常生活中解决许多问题的有效模型,我们要善于利用列一元二次方程求解这个数学模型解决实际生活中的各种问题,并注意要根据实际意义进行解释和检验,从中体会数学建模的思想方法.
(6)检验:列方程解应用题时,要对所求出的未知数进行检验,检验的目的有两个:其一,检验求出来的未知数的值是否满足方程;其二,检验求出的未知数的值是不是满足实际问题的要求,对于适合方程而不适合实际问题的未知数的值应舍去;
(7)答:就是写出答案,其中在书写时还要注意不要漏写单位名称.当x=10时, =12.5; 当x=25时, =5.均合题意 例1、如图,有一矩形空地,一边靠墙,这堵墙的长为30m,另三
边由一段长为35m的铁丝网围成.已知矩形空地的面积是125m2,
求矩形空地的长和宽.分析:根据长方形面积公式,运用长×宽=125列出方程,即可求
得答案.在方程中墙壁的长度30m没有直接用到,但在检验结果
的时候,要注意矩形的平行于墙壁的一边长不能超过30m,否则,
这堵墙就没有作为养鸡场的利用价值。根据题意,得 解:设矩形与墙平行的一边长为xm,则矩形的另一条边长为 m.整理,得x2-35x+250=O.答:矩形空地的长和宽分别是12.5m和10m或25m和5m解这个方程,得x1=10,x2=25. (一)几何中面积、长度问题例2 如图所示,一架长为10 m的梯子斜靠在墙上,梯子的顶端A处到地面的距离为8 m,如果梯子的顶端沿墙面下滑2 m,那么梯子的底端在地面上滑动的距离是多少? 分析:如图所示,此题的相等关系是矩形面积减去道路面积等于540m2.小结
1.解法二和解法一相比更简单,它利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,可以使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路).2.有些同学在列方程解应用题时,往往看到正解就保留,看到负解就舍去.其实,即使是正解也要根据题设条件进行检验,该舍就舍.此题一定要注意原矩形“宽为20 m、长为32 m”这个条件,从而进行正确取舍.总结解决此类问题 必须具备良好的几何概念知识,熟悉长度,面积,体积等公式。
有时需要通过平移的方法来解决问题。
常见问题:挖沟的宽度,制作盒子。1、用20cm长的铁丝能否折成面积为30cm2的矩形,若能够,求它的长与宽;若不能,请说明理由.练习:解:设这个矩形的长为xcm,则宽为 cm,即x2-10x+30=0这里a=1,b=-10,c=30,∴此方程无解.∴用20cm长的铁丝不能折成面积为30cm2的矩形.练习:1.如图,用长为18m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.要围成苗圃的面积为81m2,应该怎么设计?解:设苗圃的一边长为xm,则化简得,答:应围成一个边长为9米的正方形.(二)数字与方程1. 一个两位数,它的十位数字比个位数字小3,而它的个位数字的平方恰好等于这个两位数.求这个两位数.2.有一个两位数,它的十位数字与个位数字的和是5.把这个两位数的十位数字与个位数字互换后得到另一个两位数,两个两位数的积为736.求原来的两位数.例1:平阳按“九五”国民经济发展规划要求,2003年的社会总产值要比2001年增长21%,求平均每年增长的百分率.(提示:基数为2001年的社会总产值,可视为a)设每年增长率为x,2001年的总产值为a,则2001年
a2002年
a(1+x)2003年
a(1+x) 2a(1+x) 2 =a+21%a分析:(三)增长率问题a (1+x) 2 =1.21 a
(1+x) 2 =1.21
1+x =1.1
x =0.1解:设每年增长率为x,2001年的总产值为a,则a(1+x) 2 =a+21%a答:平均每年增长的百分率为10% .例2 . 某市为了解决市民看病难的问题,决定下调药品的价格.某种药品经过连续两次降价后,由每盒200元下调至128元,求这种药品平均每次降价的百分率是多少?总结1.平均增长率问题中的基本数量关系为
A(1+X)n=B(A为始量,B为终止量,n为增长的次数,x为平均增长率)
类似的还有平均降低率问题中的基本数量关系为A(1-X)n=B(A为始量,B为终止量,n为降低的次数,x为平均降低率)
2.对于“增长率”问题,如人口的减少、利率的降低、汽车的折旧等等,都是在原来基数上减少,不能与一般性的增加和减少相混淆.练习:1.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程
为 .B4(四)储蓄问题例1.王老师把500元钱按一年定期存入银行,到期后,取出了300元捐给了灾区,剩下的200元和应得的利息又全部按一年定期存入,由于利息下调,第二次存款的年利率是第一次存款年利率的 ,这样到期后可得利息15元,求第一次存款的年利率 解:第一次存款的年利率为x,根据题意,可得方程: 整理,得20x2+8x-1=0. 解得x1=0.1=10%,x2=-0.5(舍去).因此第一次存款的年利率是10%例1. 某商场销售一批名牌衬衫,平均每天可销售出20件,每件盈利40元,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.若商场平均每天要盈利1200元,每件衬衫应降价多少元?(五)销售问题分析:这类销售问题,涉及的数量关系比较多,我们可以通过列表的方式来分析其中的数量关系.204080020+2x 40-x 1200例2 (2010南京)某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一性清仓,清仓时单价为40元.设第二个月单价降低x元.(1)填表(不需化简):(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?分析:800-200-(200+10x) 80-x 200+10x1. 某汽车在公路上行驶,它的路程s(m)和时间t(s)之间的关系为:s=10t+3t2,那么行驶 200m需要多长时间?(六)运动与方程例1 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发,几秒后⊿ PBQ的面积等于8cm2?解:设x秒后⊿ PBQ的面积等于8cm2
根据题意,得
整理,得
解这个方程,得所以2秒或4秒后⊿ PBQ的面积等于8cm2例2:等腰直角⊿ ABC中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,通过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2?例1 有一根长为120 cm的绳子.
(1)能否围成一个面积是500 cm2的矩形?
(2)能否围成一个面积是1000 cm2的矩形?(八)假设存在问题分析:在解决这一类存在问题时,一般先假设
面积是500 cm2和1000 cm2的矩形存在,再根据题意列出方程求解.如果方程有解,就说明符合条件的矩形存在;如果方程无解,则说明符合条件的矩形不存在.小结例: 在一次聚会中,每两个参加聚会的人都相互握了一次手,一共握了45次手,问参加这次聚会的人数是多少?(九)统计问题分析:对这个问题,我们可以作这样的假设:如果有x个人参加聚会,那么第1个人需要与除他自己以外的其他(x-1)个人握手,要握(x-1)次手;第2个人也分别与其他(x-1)个人握手,可握(x-1)次手;……;依此类推,第x个人同样要与其他(x-1)个人握手,可握(x-1)次手,如此共有x(x-1)次握手,显然此时每两人之间都按握了两次手进行计算的.所以,按照题意,可得2(1)x(x-1)=45次手.
练习
某旅行团结束旅行,其中建议大家互相告别,细心的小明发现,每两个参加旅行的人相互握手一次,共握手66次,问这次旅行的人有多少?1.列方程解实际问题,一般分为审题、找等量关系式、设未知数、列方程、解方程、检验、写出答案这六步进行,其中审题过程虽在草稿纸上进行,但这一步非常重要,只有经过认真审题,分清已知条件和所求量,明确量与量之间的数量关系,才能准确找出相等关系,列出方程.?【方法总结】2.在列一元二次方程解实际问题时还要注意一些关键的词语,如“多”、“倍”、“差”、“提前”、“同时”、“早到”、“迟到”、“增加几倍”等. 3.在解决复杂问题时,我们可以借助于列表格等辅助方式弄清题目中的数量关系,列出方程.4.一元二次方程是我们日常生活中解决许多问题的有效模型,我们要善于利用列一元二次方程求解这个数学模型解决实际生活中的各种问题,并注意要根据实际意义进行解释和检验,从中体会数学建模的思想方法.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
