数学九年级下青岛版5.1函数与它的表示法课件2
文档属性
| 名称 | 数学九年级下青岛版5.1函数与它的表示法课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 586.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 00:00:00 | ||
图片预览








文档简介
课件25张PPT。§5.1 函数与它的表示法(1)第5章 对函数的再探索复习1:常量与变量什么叫常量?在一个过程中,固定不变的量称为常量.什么叫变量?在一个过程中,可以取不同数值的量称为变量.⒉圆周长C与圆的半径r之间的关系式是 C=2πr,其中常量是 ________,
变量是 _______ 。⒈某水果店橘子的单价为2.5元/千克,买K千 克橘子的总价为S元,其中常量是________,变量是 ___________。⒊声音在空气中传播的速度v(m/s)与温度t(0C)之间的关系式是v=331+0.6t,其中常量是————————————,变量是—————。2.5元/千克K,S2,πC, r331,0.6V,t练习指出下列事件过程中的常量与变量下图是某城市的海滨浴场波浪的浪高与时间的变化曲线图,你能找出其中的变量吗? 小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬16元/时计算,设小明的哥哥这个月工作的时间为 t 时,应得报酬为 m 元.怎样用关于 t 的代数式来表示m? 填写下表:
表7-1 在以下问题中,哪些是变量?哪些是常量?16t8032024016016 m = 16 t 上面各问题中两个变量 (t 与 m, s 与 v) 之间关系的有什么共同点吗? m = 16 ts = 0.085v2概念: 一般地,在某个变化过程中,设有两个变量 x, y,如果对于 x 的每一个确定的值, y 都有唯一确定的值, 那么就说 y 是 x 的函数, x 叫做自变量.m是t的函数,t是自变量。s是v的函数,v是自变量。函数解析式复习2:函数对于函数m=7.8t,当t=5时,能求得m的值吗?怎么求?函数值:在这里,我们把m=39叫做当自变量t=5 时的函数值。把它代入函数解析式,得
m=7.8t=7.8×5=39
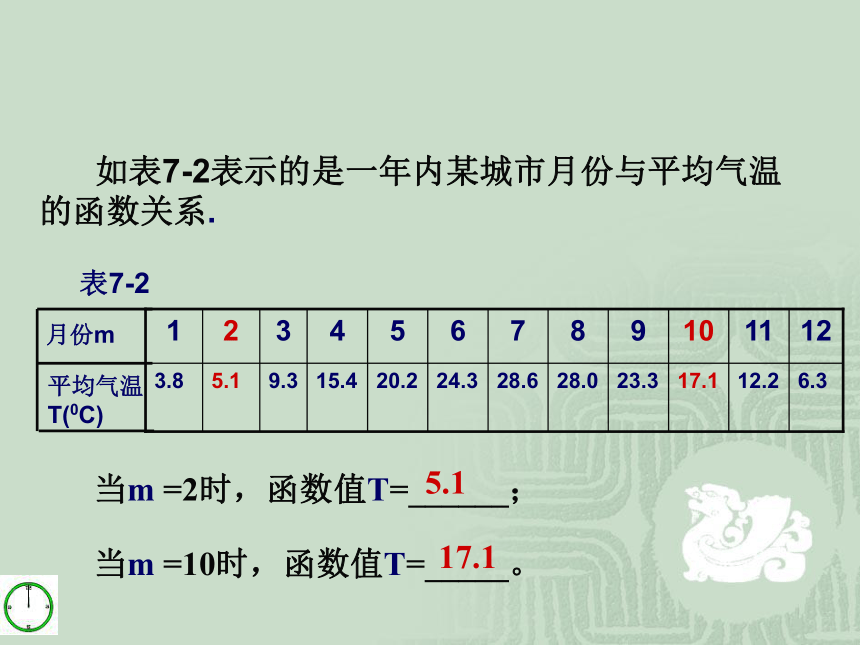
请你思考函数值概念 如表7-2表示的是一年内某城市月份与平均气温的函数关系. 当m =2时,函数值T=______;
当m =10时,函数值T=_____。5.117.1x轴或横轴y轴或纵轴原点平面直角坐标系第一象限第二象限第三象限第四象限注 意:坐标轴上的点不属于任何象限。复习3:平面直角坐标系1.由点找坐标:如何表示点A的位置?A(4,3)
如何表示点A的位置:
过点A作x轴的垂线,垂足在x轴上对
应的数是4,就是点A的横坐标.
过点A作y轴的垂线,垂足在y轴上对
应的数是3,就是点A的纵坐标.
有序数对(4,3)就是点A的坐标.
xy在平面直角坐标系中找到表示A(3,-2)的点.2.由坐标找点由坐标找点的方法:
先找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。A我们来探究函数y=x-1的图像.
(1)给定自变量的x的一些值,求出对应y的值,并填表;
(2)以x与y的对应职位点的坐标描出这些点;
(3)按照自变量由小到大的顺序把描出的点顺次连接起来.
如图,可得函数y=x-1的图像.
用描点法画函数图像的步骤:①列表 ②描点 ③连线复习4:在平面直角坐标系内画函数图像 1、若y=kx+b (k、b是常数,且k ),则y叫做x 的_____
函数;当b=0时,一次函数就是_______函数。 2、一次函数y=2x-1的图
象是一条经过点(0,____)和
(____ ,0)且平行于直线
__________的直线。Y=2xY=2x-1一次正比例-1y=2x 3、一次函数y=kx+b的
图象是一条经过点(0,___)
和(____,0)且平行于直线
_______的直线。by=kx复习4:一次函数与它的图像一般地,一次函数y=kx+b有下列性质:
(1)当k>0时,y随x的增大而增大,图象是向右上升的直线;
(2)当k<0时,y随x的增大而减小,图象是向右下降的直线。
Y=kx+b(k>0)Y=kx+b(k<0)(1)函数y=3x+2的图象是一条向右 ______
的直线,且y随x的增大而________;图像过第几象限?
(2)函数y=-x-1的图象是一条向右 _______
的直线,且y随x的增大而 ________。图像过第几象限?
一次函数图像升降变化和它所在的象限与什么有关?
上升增大下降减小表示函数关系的方法(1)用数学式子表示函数的方法叫做解析法(2)用表格表示函数关系的方法叫做列表法(3)用图象表示函数关系的方法叫做图像法用来表达函数关系的数学式子叫做函数解析式或
函数关系式思考列表法解析法图像法用描点法画函数图像时用到了函数关系的
哪几种表示方法?
(1)在这个问题中,速度y与
时间t之间的函数关系是用
哪种方法表示的?(2)时间t的取值范围是
什么?图像法0≤t≤71.一辆汽车在行驶中,速度v随时
间t变化的情况如图所示.
t=4v=30t=0或t=7(3)当时间t为何值时,汽车行
驶的速度最大?最大速度是多少?
当时间t取何值时,速度为0?(4)在哪一时间段汽车的
行驶速度逐渐增加?在哪
一时间段汽车的行驶速度
逐渐减少?在那一时间段
按匀速运动行驶?
0≤t≤4
1≤t≤2
4≤t≤7
根据图像,填写下表:0202025301550S=解析法2.如图,正三角形ABC内接与
圆O,设圆的半径为r。试写
出图 中阴影部分的面积S与
r的函数 关系,它们之间的
函数关系是用哪种方法表示的?
1.表示函数关系的方法共有三种:
课堂小结分别是 (1)解析法
(2)列表法
(3)图像法2.三种方法都有优点和不足,用哪种方法,
视具体情况而定1、画出函数y=- 3x-1的图像
2.下列各点在函数y=-3x-1的图像上的是( )
A.(1,4) B.(-1,-3) C.(-1,-2) D.(1,-4)
3.当点(2,m)在函数S=x2 的图像上,则m=——. 课堂检测4.某天早晨,小明离家跑步到公园锻炼一会后又
回到家里.下面图像中,能反映小明离家的距离
y和时间x的函数关系的是( ).5.下列各点哪些在函数y=2x-1的图像上?
A(1,- 2) B(-2.5,-6) C(0,-1)
D(101,199)E(-100,-103)F(1.5,2)
变量是 _______ 。⒈某水果店橘子的单价为2.5元/千克,买K千 克橘子的总价为S元,其中常量是________,变量是 ___________。⒊声音在空气中传播的速度v(m/s)与温度t(0C)之间的关系式是v=331+0.6t,其中常量是————————————,变量是—————。2.5元/千克K,S2,πC, r331,0.6V,t练习指出下列事件过程中的常量与变量下图是某城市的海滨浴场波浪的浪高与时间的变化曲线图,你能找出其中的变量吗? 小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬16元/时计算,设小明的哥哥这个月工作的时间为 t 时,应得报酬为 m 元.怎样用关于 t 的代数式来表示m? 填写下表:
表7-1 在以下问题中,哪些是变量?哪些是常量?16t8032024016016 m = 16 t 上面各问题中两个变量 (t 与 m, s 与 v) 之间关系的有什么共同点吗? m = 16 ts = 0.085v2概念: 一般地,在某个变化过程中,设有两个变量 x, y,如果对于 x 的每一个确定的值, y 都有唯一确定的值, 那么就说 y 是 x 的函数, x 叫做自变量.m是t的函数,t是自变量。s是v的函数,v是自变量。函数解析式复习2:函数对于函数m=7.8t,当t=5时,能求得m的值吗?怎么求?函数值:在这里,我们把m=39叫做当自变量t=5 时的函数值。把它代入函数解析式,得
m=7.8t=7.8×5=39
请你思考函数值概念 如表7-2表示的是一年内某城市月份与平均气温的函数关系. 当m =2时,函数值T=______;
当m =10时,函数值T=_____。5.117.1x轴或横轴y轴或纵轴原点平面直角坐标系第一象限第二象限第三象限第四象限注 意:坐标轴上的点不属于任何象限。复习3:平面直角坐标系1.由点找坐标:如何表示点A的位置?A(4,3)
如何表示点A的位置:
过点A作x轴的垂线,垂足在x轴上对
应的数是4,就是点A的横坐标.
过点A作y轴的垂线,垂足在y轴上对
应的数是3,就是点A的纵坐标.
有序数对(4,3)就是点A的坐标.
xy在平面直角坐标系中找到表示A(3,-2)的点.2.由坐标找点由坐标找点的方法:
先找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。A我们来探究函数y=x-1的图像.
(1)给定自变量的x的一些值,求出对应y的值,并填表;
(2)以x与y的对应职位点的坐标描出这些点;
(3)按照自变量由小到大的顺序把描出的点顺次连接起来.
如图,可得函数y=x-1的图像.
用描点法画函数图像的步骤:①列表 ②描点 ③连线复习4:在平面直角坐标系内画函数图像 1、若y=kx+b (k、b是常数,且k ),则y叫做x 的_____
函数;当b=0时,一次函数就是_______函数。 2、一次函数y=2x-1的图
象是一条经过点(0,____)和
(____ ,0)且平行于直线
__________的直线。Y=2xY=2x-1一次正比例-1y=2x 3、一次函数y=kx+b的
图象是一条经过点(0,___)
和(____,0)且平行于直线
_______的直线。by=kx复习4:一次函数与它的图像一般地,一次函数y=kx+b有下列性质:
(1)当k>0时,y随x的增大而增大,图象是向右上升的直线;
(2)当k<0时,y随x的增大而减小,图象是向右下降的直线。
Y=kx+b(k>0)Y=kx+b(k<0)(1)函数y=3x+2的图象是一条向右 ______
的直线,且y随x的增大而________;图像过第几象限?
(2)函数y=-x-1的图象是一条向右 _______
的直线,且y随x的增大而 ________。图像过第几象限?
一次函数图像升降变化和它所在的象限与什么有关?
上升增大下降减小表示函数关系的方法(1)用数学式子表示函数的方法叫做解析法(2)用表格表示函数关系的方法叫做列表法(3)用图象表示函数关系的方法叫做图像法用来表达函数关系的数学式子叫做函数解析式或
函数关系式思考列表法解析法图像法用描点法画函数图像时用到了函数关系的
哪几种表示方法?
(1)在这个问题中,速度y与
时间t之间的函数关系是用
哪种方法表示的?(2)时间t的取值范围是
什么?图像法0≤t≤71.一辆汽车在行驶中,速度v随时
间t变化的情况如图所示.
t=4v=30t=0或t=7(3)当时间t为何值时,汽车行
驶的速度最大?最大速度是多少?
当时间t取何值时,速度为0?(4)在哪一时间段汽车的
行驶速度逐渐增加?在哪
一时间段汽车的行驶速度
逐渐减少?在那一时间段
按匀速运动行驶?
0≤t≤4
1≤t≤2
4≤t≤7
根据图像,填写下表:0202025301550S=解析法2.如图,正三角形ABC内接与
圆O,设圆的半径为r。试写
出图 中阴影部分的面积S与
r的函数 关系,它们之间的
函数关系是用哪种方法表示的?
1.表示函数关系的方法共有三种:
课堂小结分别是 (1)解析法
(2)列表法
(3)图像法2.三种方法都有优点和不足,用哪种方法,
视具体情况而定1、画出函数y=- 3x-1的图像
2.下列各点在函数y=-3x-1的图像上的是( )
A.(1,4) B.(-1,-3) C.(-1,-2) D.(1,-4)
3.当点(2,m)在函数S=x2 的图像上,则m=——. 课堂检测4.某天早晨,小明离家跑步到公园锻炼一会后又
回到家里.下面图像中,能反映小明离家的距离
y和时间x的函数关系的是( ).5.下列各点哪些在函数y=2x-1的图像上?
A(1,- 2) B(-2.5,-6) C(0,-1)
D(101,199)E(-100,-103)F(1.5,2)
