数学九年级下青岛版5.1函数与它的表示法课件4
文档属性
| 名称 | 数学九年级下青岛版5.1函数与它的表示法课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 978.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 08:40:50 | ||
图片预览








文档简介
课件26张PPT。§5.1 函数与它的表示法(1)第5章 对函数的再探索观察与思考 你还记得什么是函数吗?在现实生活中,函数关系是处处存在的。
你知道表示函数关系的方法通常有哪几种吗?
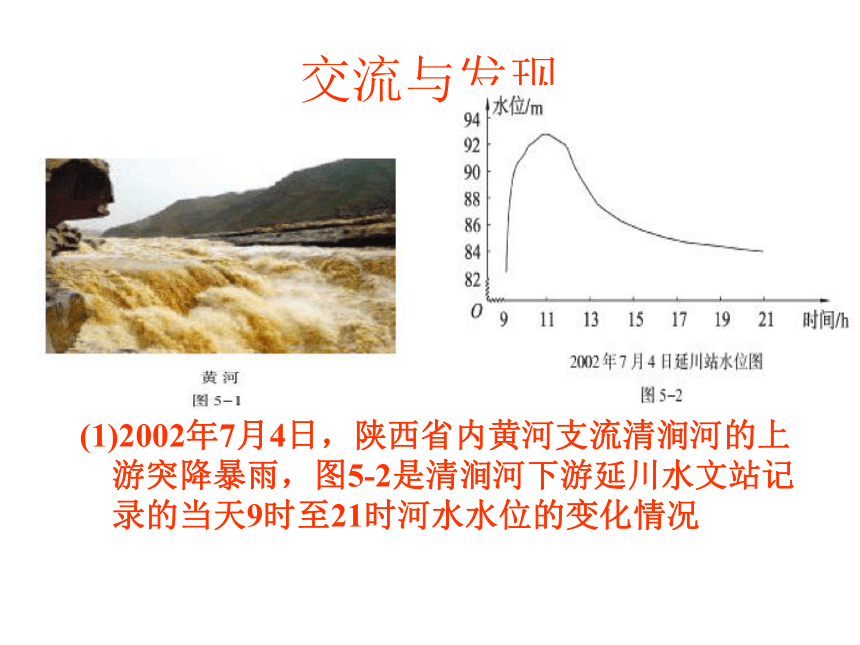
交流与发现(1)2002年7月4日,陕西省内黄河支流清涧河的上游突降暴雨,图5-2是清涧河下游延川水文站记录的当天9时至21时河水水位的变化情况交流与发现 在图5-2中,河水水位与时间的函数关系是用什么
方法表示的?你能看出那一时刻河水的水位最高吗?最高水位是多少?当天17时的河水水位是多少?11时93m85m交流与发现y与x之间的函数关系是用什么方法表示的?(2)一根弹簧原长15cm,在弹性限度内,每增加10N的拉力,弹簧就伸长2cm,请你填写下表:01719212325交流与发现h与t之间的函数关系是用什么方法表示的?当t=0(s)和t=1(s)时,对应的h值分别是多少?04.9(3)物体自由下落的高度h(m)与时间t(s)
之间的函数关系是h=4.9t2
表示函数关系的方法(1)用数学式子表示函数的方法叫做解析法(2)用表格表示函数关系的方法叫做列表法(3)用图象表示函数关系的方法叫做图像法用来表达函数关系的数学式子叫做函数解析式或
函数关系式交流与探究上述的例子中,(1)(2)(3)分别是哪种表示
函数的方法呢?(1)是 图像法(2)是列表法(3)是解析法你能试着举出用这三种方法表示函数的例子吗?两个变量间的函数关系,可有
不同的表示方法,上面的三方
法在解决具体问题时,都有广
泛的应用.思考列表法解析法图像法用描点法画函数图像时用到了函数关系的
哪几种表示方法?
进一步研究以上三个例子,思考下列问题:(1)在这些问题中,自变量可以取值的范围
分别是什么? (2)对于自变量在它可以取值的范围内每取
一个值,另一个变量是否都有惟一确定的
值与它对应?(3)由此你对函数有了哪些进一步的认识?
与同学交流.结论:
函数定义
在同一个变化过程中,有两个变量x,y. 如果对于变量x在可以取值的范围内每取 一个确定值,变量y都有一个惟一确定的值与它对应,那么就说y是x的函数.例1 求下列函数中自变量x可以取值的范围:(1) y=3x-2(2) y=(3)y=(4) y=x取任意实数x≥1x<(2) y=例2 一根蜡烛长20cm,每小时燃掉5cm.(1)写出蜡烛剩余的长度y(cm)与燃烧时间x(h)
之间的函数解析式.(2)求自变量x可以取值的范围;(3)蜡烛点燃2h后还剩多长?y=20-5x0≤x ≤410cm练习1: 求下列函数中自变量x可以取值的范围:(1) y=(2) y= (3) y=(4) y=(2) y=x为任意实数x≠x≤3x>练习2: 等腰三角形ABC的周长为10cm,底边BC长为y(cm),
腰AB长为x(cm)
(1)写出y与x之间的函数解析式;(2)指出自变量x可以取值的范围.y=10-2x2.5<x<5xyx练习3: 油箱中有油300L,油从管道中匀速流出,1小时流完.
写出油箱中剩余的油量Q(L)与油流出时间t(s)之间
的函数解析式,并指出自变量t 可以取值的范围.函数解析式:Q=300-5tt的取值范围: 0≤t≤60(1)在这个问题中,速度y与
时间t之间的函数关系是用
哪种方法表示的?(2)时间t的取值范围是
什么?图像法0≤t≤71.一辆汽车在行驶中,速度v随时
间t变化的情况如图所示.
t=4v=30t=0或t=7(3)当时间t为何值时,汽车行
驶的速度最大?最大速度是多少?
当时间t取何值时,速度为0?(4)在哪一时间段汽车的
行驶速度逐渐增加?在哪
一时间段汽车的行驶速度
逐渐减少?在那一时间段
按匀速运动行驶?
0≤t≤4
1≤t≤2
4≤t≤7
根据图像,填写下表:0202025301550S=∏解析法2.如图,正三角形ABC内接与
圆O,设圆的半径为r。试写
出图 中阴影部分的面积S与
r的函数 关系,它们之间的
函数关系是用哪种方法表示的?
1.表示函数关系的方法共有三种:
课堂小结分别是 (1)解析法
(2)列表法
(3)图像法2.三种方法都有优点和不足,用哪种方法,
视具体情况而定课堂小结 确定函数自变量可以取值的范围时,
必须使函数解析式有意义.在解决实际
问题时,还要使实际问题有意义.作业课本P8 A组 1、2题
同学们再见
你知道表示函数关系的方法通常有哪几种吗?
交流与发现(1)2002年7月4日,陕西省内黄河支流清涧河的上游突降暴雨,图5-2是清涧河下游延川水文站记录的当天9时至21时河水水位的变化情况交流与发现 在图5-2中,河水水位与时间的函数关系是用什么
方法表示的?你能看出那一时刻河水的水位最高吗?最高水位是多少?当天17时的河水水位是多少?11时93m85m交流与发现y与x之间的函数关系是用什么方法表示的?(2)一根弹簧原长15cm,在弹性限度内,每增加10N的拉力,弹簧就伸长2cm,请你填写下表:01719212325交流与发现h与t之间的函数关系是用什么方法表示的?当t=0(s)和t=1(s)时,对应的h值分别是多少?04.9(3)物体自由下落的高度h(m)与时间t(s)
之间的函数关系是h=4.9t2
表示函数关系的方法(1)用数学式子表示函数的方法叫做解析法(2)用表格表示函数关系的方法叫做列表法(3)用图象表示函数关系的方法叫做图像法用来表达函数关系的数学式子叫做函数解析式或
函数关系式交流与探究上述的例子中,(1)(2)(3)分别是哪种表示
函数的方法呢?(1)是 图像法(2)是列表法(3)是解析法你能试着举出用这三种方法表示函数的例子吗?两个变量间的函数关系,可有
不同的表示方法,上面的三方
法在解决具体问题时,都有广
泛的应用.思考列表法解析法图像法用描点法画函数图像时用到了函数关系的
哪几种表示方法?
进一步研究以上三个例子,思考下列问题:(1)在这些问题中,自变量可以取值的范围
分别是什么? (2)对于自变量在它可以取值的范围内每取
一个值,另一个变量是否都有惟一确定的
值与它对应?(3)由此你对函数有了哪些进一步的认识?
与同学交流.结论:
函数定义
在同一个变化过程中,有两个变量x,y. 如果对于变量x在可以取值的范围内每取 一个确定值,变量y都有一个惟一确定的值与它对应,那么就说y是x的函数.例1 求下列函数中自变量x可以取值的范围:(1) y=3x-2(2) y=(3)y=(4) y=x取任意实数x≥1x<(2) y=例2 一根蜡烛长20cm,每小时燃掉5cm.(1)写出蜡烛剩余的长度y(cm)与燃烧时间x(h)
之间的函数解析式.(2)求自变量x可以取值的范围;(3)蜡烛点燃2h后还剩多长?y=20-5x0≤x ≤410cm练习1: 求下列函数中自变量x可以取值的范围:(1) y=(2) y= (3) y=(4) y=(2) y=x为任意实数x≠x≤3x>练习2: 等腰三角形ABC的周长为10cm,底边BC长为y(cm),
腰AB长为x(cm)
(1)写出y与x之间的函数解析式;(2)指出自变量x可以取值的范围.y=10-2x2.5<x<5xyx练习3: 油箱中有油300L,油从管道中匀速流出,1小时流完.
写出油箱中剩余的油量Q(L)与油流出时间t(s)之间
的函数解析式,并指出自变量t 可以取值的范围.函数解析式:Q=300-5tt的取值范围: 0≤t≤60(1)在这个问题中,速度y与
时间t之间的函数关系是用
哪种方法表示的?(2)时间t的取值范围是
什么?图像法0≤t≤71.一辆汽车在行驶中,速度v随时
间t变化的情况如图所示.
t=4v=30t=0或t=7(3)当时间t为何值时,汽车行
驶的速度最大?最大速度是多少?
当时间t取何值时,速度为0?(4)在哪一时间段汽车的
行驶速度逐渐增加?在哪
一时间段汽车的行驶速度
逐渐减少?在那一时间段
按匀速运动行驶?
0≤t≤4
1≤t≤2
4≤t≤7
根据图像,填写下表:0202025301550S=∏解析法2.如图,正三角形ABC内接与
圆O,设圆的半径为r。试写
出图 中阴影部分的面积S与
r的函数 关系,它们之间的
函数关系是用哪种方法表示的?
1.表示函数关系的方法共有三种:
课堂小结分别是 (1)解析法
(2)列表法
(3)图像法2.三种方法都有优点和不足,用哪种方法,
视具体情况而定课堂小结 确定函数自变量可以取值的范围时,
必须使函数解析式有意义.在解决实际
问题时,还要使实际问题有意义.作业课本P8 A组 1、2题
同学们再见
