数学九年级下青岛版5.7二次函数的应用课件3
文档属性
| 名称 | 数学九年级下青岛版5.7二次函数的应用课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 351.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 08:45:18 | ||
图片预览










文档简介
课件30张PPT。二次函数的应用学习目标:
1、能分析和表示不同实际背景下的二次函数关系,并利用二次函数的知识解决实际问题。
2、理解如何运用二次函数的性质求实际问题中的最大值或最小值目标导航二次函数解析式的一般形式是______________
化成y=a(x-h)2+k的形式为___________________
当横坐标为____时,纵坐标有最大(小)值_______
y=ax2+bx+c(a≠0)y=(x+ )+y=a(x+ )2+y=a(x+ )2+教师引领例1.修建有一条边靠墙的矩形菜园,不靠墙的的三边的长度之
和为60m.应怎样设计才使菜园面积最大?最大面积是多少?解:如图,设菜园的宽为x(m),矩形菜园的面积为y(m2)则菜园的长为(60-2 x )(m)依题意y与x之间的函数解析式为
y=x(60-2x)
二次函数与最大菜园面积x60-2xy =- 2x2+60x
=-2(x2-30x+225-225)
=-2(x2-30x+225)-225×(-2)
=-2(x-15) 2 +450
∵a=-2﹤0 ∴当x=15时,y有最大值,最大值是450
所以,当菜园的宽为15 m时菜园面积最大。最大面积是450m2 交流与思考: 如何运用二次函数求实际问题中的最大值或最小值?如何运用二次函数求实际问题中的最大值或最小值? 交流思考 首先应当求出函数解析式和自变量的取值范围,
然后通过配方变形,或利用公式求它的最大值或最小值。 注意:由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。例2:如图,ABCD是一块边长为2 m的正方形铁板,在边AB上选取一点M,分别以AM和MB为边截取两块相邻的正方形板料。当AM的长为何值时,截取的板料面积最小?D小组展示二次函数与最小板料面积解:设AM的长为x(m),则BM的长为(2-x)m,以AM和MB为边的两块正方形面积之和为y.依题意得y与x之间的函数解析式为
y=x2+(2-x)2 =2x2-4x+4
=2(x2-2x)+4
=2(x2-2x+1-1)+4
=2(x-1)2+2
∵a=2>0∴当x=1时,y有最小值,最小值为2.
所以,当AM的长为1m时,截取的板料面积最小,最小面积为2m2.
当x=____________时,
二次函数y=ax2+bx+c有最大(小)值
_____________
教师点拨1、已知二次函数y=2(x-2)2+1,当x=__时,y取最___值,是___.
2、二次函数y=-2(x-4)2+1的图像开口____,当x=__时,y取最___值,是___.达标检测2小1下4大13、某广告公司要设计一个周长为20m的矩形广告牌,当矩形的一边为何值时,广告牌的面积最大?解设矩形的一边为x(m),则另一边为(10-x)m,矩形的面积为ym2,根据题意,y与x之间的函数解析式为y=x(10-x) y=-x2+10x
=-(x-5)2+25
∵a=-1<0 ∴当x=5时,y有最大值,最大值为25.
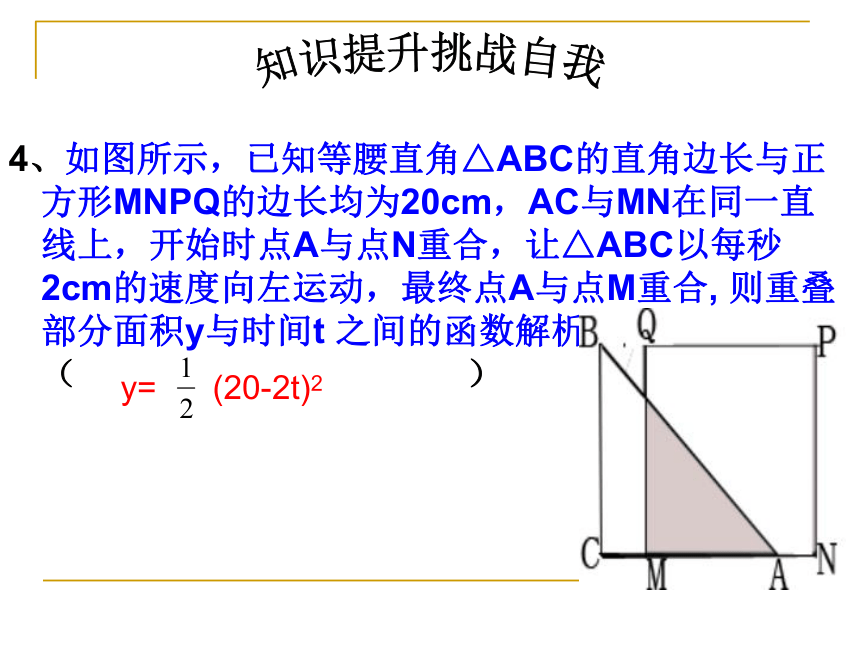
所以,当矩形的一边长为5m时,广告牌面积最大,最大面积为25m24、如图所示,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合, 则重叠部分面积y与时间t 之间的函数解析式为( )y= (20-2t)2知识提升挑战自我如图所示,阳光中学教学楼前喷
水池喷出的抛物线形水柱,
其解析式为 y=-x2+4x+2 ,
则水柱的最大高度是( )。
A、2 B、4 C、6 D、7
拓展延伸C实际问题 数学问题求解数学问题小结1、如图所示,阳光中学教学楼前喷
水池喷出的抛物线形水柱,其解析
式为 ,则水柱的最大高
度是()。
A、2 B、4 C、6 D、2+
2、已知二次函数y=ax2+bx+c 的图像如图所示,有下列4个结论:
①abc>0; ②b0;
④2c<3b; 其中正确的结论有:
A、2个 B、3个 C、4个 D、1个
知 识 提 升 挑 战 自 我我 收 获 我 满 意总结规律 事半功倍我学习,我快乐探究一y-2x=1y=2x+1(1,3)探究二在同一个直角坐标系中,画出
函数y=-2x+6与y=3x+1的图像
1、找出它们的交点P,写出点P的坐标。2、点P的坐标适合方程2x+y=6吗?
适合方程3x-y=-1吗?为什么?4、用画函数图象的方法, 解二元一次方程组的主要步骤是什么?xyo-123456789-2-3112345-1-2-367y=-2x+6y=3x+1P(1,4) 用画函数图象的方法 解二元一次方程组的主要步骤:
题后反思规律在现 1、变成函数式 2、画图像
3、找交点 4、写出解解:由x+y=5,得y=-x+5.
由5x-2y=4,得y= x-2.
在同一直角坐标系中,画出一次函数y=-x+5与y= x-2的图像。
因为两条直线相交于点(2,3),
所以原方程组的解是例题解答探究三尝试即成x/(元/件)
y/件o120100120140例2、某商店试销一种运动服,经市场调查,发现平均日销量y(件)是销售单价x(元/件)的一次函数,其图像如图所示。
1、根据图像,求y与x
之间的函数关系式;
2、当销售单价为多少元
时,平均日销量是150件? 如图,已知函数y=ax+b和y=kx的图像交于点P,则根据图像可得关于x、 y的二元一次方
程组 的解是试一试-4-2oy=kxy=ax+bxy图像的妙用
不解方程组,根据图像判断方程
组 的解的符号情况?
图像真妙开动脑筋延伸训练师生小结作业课后作业:教科书83页练习3题。
二元一次方程组 的解可以看做
是哪两个一次函数的交点坐标?
议一议看谁最仔细(y= x+1和y=2x-2)xyo-123456789-2-3112345-1-2-367y=-2x+6y=3x+1P(1,4)xyo-123456789-2-3-4-5-6-7-8-9112345-1-2-3-4-567yxo2-4-242466-212.3图像的妙用莘县国棉中学 樊启彦作业布置:1、课本第48页作业题:
1、 2。
谢谢大家!
祝您愉快!
1、能分析和表示不同实际背景下的二次函数关系,并利用二次函数的知识解决实际问题。
2、理解如何运用二次函数的性质求实际问题中的最大值或最小值目标导航二次函数解析式的一般形式是______________
化成y=a(x-h)2+k的形式为___________________
当横坐标为____时,纵坐标有最大(小)值_______
y=ax2+bx+c(a≠0)y=(x+ )+y=a(x+ )2+y=a(x+ )2+教师引领例1.修建有一条边靠墙的矩形菜园,不靠墙的的三边的长度之
和为60m.应怎样设计才使菜园面积最大?最大面积是多少?解:如图,设菜园的宽为x(m),矩形菜园的面积为y(m2)则菜园的长为(60-2 x )(m)依题意y与x之间的函数解析式为
y=x(60-2x)
二次函数与最大菜园面积x60-2xy =- 2x2+60x
=-2(x2-30x+225-225)
=-2(x2-30x+225)-225×(-2)
=-2(x-15) 2 +450
∵a=-2﹤0 ∴当x=15时,y有最大值,最大值是450
所以,当菜园的宽为15 m时菜园面积最大。最大面积是450m2 交流与思考: 如何运用二次函数求实际问题中的最大值或最小值?如何运用二次函数求实际问题中的最大值或最小值? 交流思考 首先应当求出函数解析式和自变量的取值范围,
然后通过配方变形,或利用公式求它的最大值或最小值。 注意:由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。例2:如图,ABCD是一块边长为2 m的正方形铁板,在边AB上选取一点M,分别以AM和MB为边截取两块相邻的正方形板料。当AM的长为何值时,截取的板料面积最小?D小组展示二次函数与最小板料面积解:设AM的长为x(m),则BM的长为(2-x)m,以AM和MB为边的两块正方形面积之和为y.依题意得y与x之间的函数解析式为
y=x2+(2-x)2 =2x2-4x+4
=2(x2-2x)+4
=2(x2-2x+1-1)+4
=2(x-1)2+2
∵a=2>0∴当x=1时,y有最小值,最小值为2.
所以,当AM的长为1m时,截取的板料面积最小,最小面积为2m2.
当x=____________时,
二次函数y=ax2+bx+c有最大(小)值
_____________
教师点拨1、已知二次函数y=2(x-2)2+1,当x=__时,y取最___值,是___.
2、二次函数y=-2(x-4)2+1的图像开口____,当x=__时,y取最___值,是___.达标检测2小1下4大13、某广告公司要设计一个周长为20m的矩形广告牌,当矩形的一边为何值时,广告牌的面积最大?解设矩形的一边为x(m),则另一边为(10-x)m,矩形的面积为ym2,根据题意,y与x之间的函数解析式为y=x(10-x) y=-x2+10x
=-(x-5)2+25
∵a=-1<0 ∴当x=5时,y有最大值,最大值为25.
所以,当矩形的一边长为5m时,广告牌面积最大,最大面积为25m24、如图所示,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2cm的速度向左运动,最终点A与点M重合, 则重叠部分面积y与时间t 之间的函数解析式为( )y= (20-2t)2知识提升挑战自我如图所示,阳光中学教学楼前喷
水池喷出的抛物线形水柱,
其解析式为 y=-x2+4x+2 ,
则水柱的最大高度是( )。
A、2 B、4 C、6 D、7
拓展延伸C实际问题 数学问题求解数学问题小结1、如图所示,阳光中学教学楼前喷
水池喷出的抛物线形水柱,其解析
式为 ,则水柱的最大高
度是()。
A、2 B、4 C、6 D、2+
2、已知二次函数y=ax2+bx+c 的图像如图所示,有下列4个结论:
①abc>0; ②b
④2c<3b; 其中正确的结论有:
A、2个 B、3个 C、4个 D、1个
知 识 提 升 挑 战 自 我我 收 获 我 满 意总结规律 事半功倍我学习,我快乐探究一y-2x=1y=2x+1(1,3)探究二在同一个直角坐标系中,画出
函数y=-2x+6与y=3x+1的图像
1、找出它们的交点P,写出点P的坐标。2、点P的坐标适合方程2x+y=6吗?
适合方程3x-y=-1吗?为什么?4、用画函数图象的方法, 解二元一次方程组的主要步骤是什么?xyo-123456789-2-3112345-1-2-367y=-2x+6y=3x+1P(1,4) 用画函数图象的方法 解二元一次方程组的主要步骤:
题后反思规律在现 1、变成函数式 2、画图像
3、找交点 4、写出解解:由x+y=5,得y=-x+5.
由5x-2y=4,得y= x-2.
在同一直角坐标系中,画出一次函数y=-x+5与y= x-2的图像。
因为两条直线相交于点(2,3),
所以原方程组的解是例题解答探究三尝试即成x/(元/件)
y/件o120100120140例2、某商店试销一种运动服,经市场调查,发现平均日销量y(件)是销售单价x(元/件)的一次函数,其图像如图所示。
1、根据图像,求y与x
之间的函数关系式;
2、当销售单价为多少元
时,平均日销量是150件? 如图,已知函数y=ax+b和y=kx的图像交于点P,则根据图像可得关于x、 y的二元一次方
程组 的解是试一试-4-2oy=kxy=ax+bxy图像的妙用
不解方程组,根据图像判断方程
组 的解的符号情况?
图像真妙开动脑筋延伸训练师生小结作业课后作业:教科书83页练习3题。
二元一次方程组 的解可以看做
是哪两个一次函数的交点坐标?
议一议看谁最仔细(y= x+1和y=2x-2)xyo-123456789-2-3112345-1-2-367y=-2x+6y=3x+1P(1,4)xyo-123456789-2-3-4-5-6-7-8-9112345-1-2-3-4-567yxo2-4-242466-212.3图像的妙用莘县国棉中学 樊启彦作业布置:1、课本第48页作业题:
1、 2。
谢谢大家!
祝您愉快!
