数学七年级上青岛版1.2几何图形课件6

(共47张PPT)
点
线
面
体
1.2几何图形
观察下面运动的图片,分别可以看成什么几何图形在运动 它们的运动又形成了什么几何图形呢
探究
点动成线
谜语 ：千条线万条线
落到水中看不见
（雨点）
你能用数学语言来描述这一现象吗？
点动成线
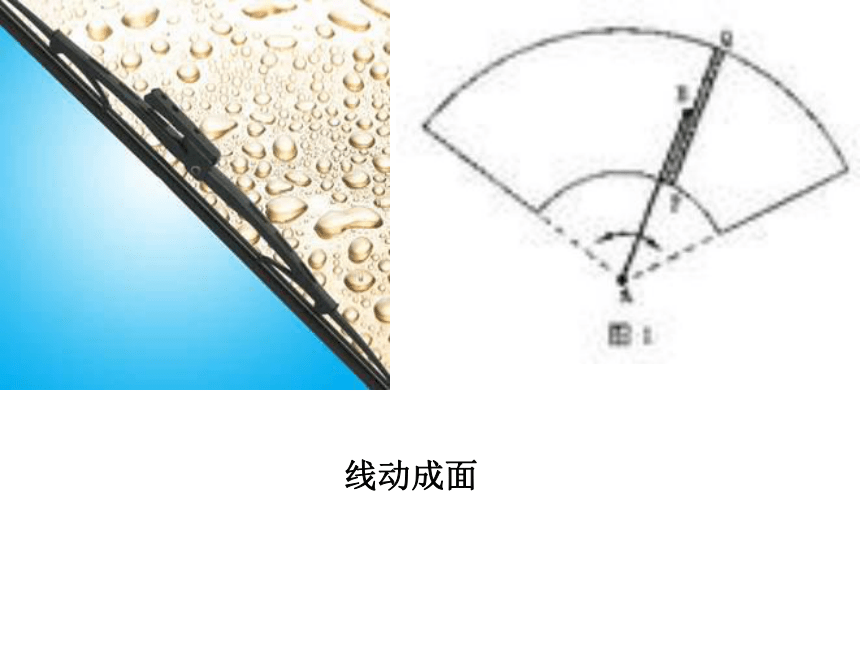
线动成面
线动成面
观察下面运动的图片,分别可以看成什么几何图形在运动 它们的运动又形成了什么几何图形呢
直角三角形绕一条直角边旋转成圆锥体
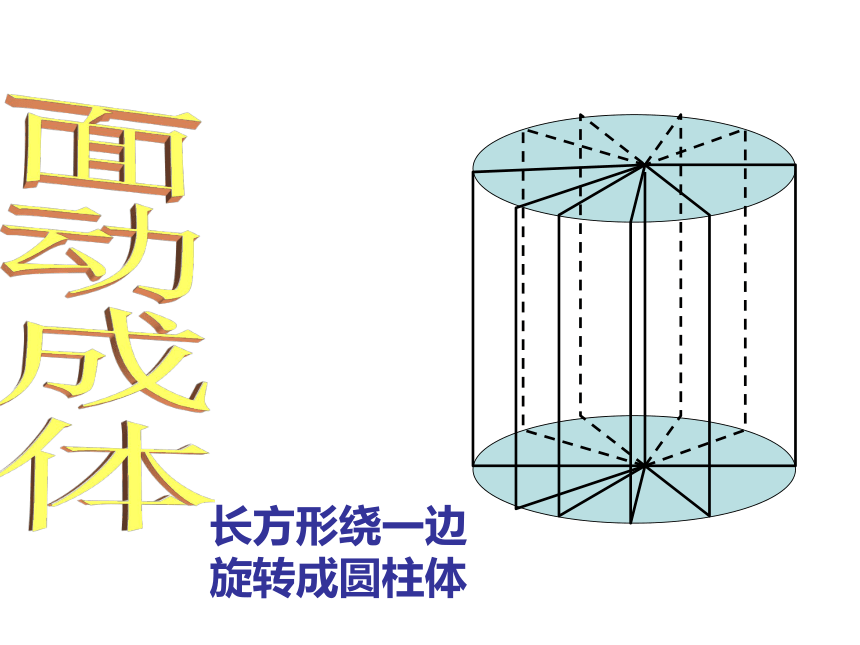
长方形绕一边旋转成圆柱体
观察下面运动的图片,分别可以看成什么几何图形在运动 它们的运动又形成了什么几何图形呢
点动成——
线动成——
面动成——
线
面
体
体是由面组成
面与面相交成线
线与线相交成点
平面图形
立方体、长方体、圆柱、圆锥、球等都是几何体，下面图中的棱柱（图1—2）、棱锥（图1—3）等也是几何体。几何体简称体。
三棱锥
三棱柱
四棱柱
五棱柱
六棱柱
四棱锥
五棱锥
六棱锥
图1—2
图1—3
点
线
面
体
—— 线与线相交而成
—— 面与面相交而成
—— 包围着体的部分
—— 物体的图形
平面几何图形
立
体
图
形
三角形
点
线段
圆
棱柱

圆柱
棱锥
圆锥
几
何
图
形
知识小结
（几何中的点无大小）
（几何中的线无粗细）
（几何中的面无厚薄）
(1)观察立体形状的包装盒，它是由哪些面组的？这些面的大小和形状都相同吗？
(2)两个面的相接处是什么图形？
(3)棱与棱的相接处是什么图形？
(4)数一数立方体有几条棱 几个顶点？
实验与探究
（5）将包装盒沿它的某些棱剪开，并铺在平面上。得到一个怎样的平面图形？如果展开的方法不同，得到的图形相同吗？动手做一做，然后画一画。你能得到多少种平面图形？与同学交流。
第一类，中间四连方，两侧各一个，共六种。
第二类，中间三连方，两侧各有一、二个，共三种。
第三类，中间二连方，两侧各有二个，只有一种。
第四类，两排各三个，只有一种。
（1）.一个正方体要剪开多少条棱才能展开成
平面图形？
正方体的展开图
（2）.一个正方体能展开成多少种平面图形？
正方体表面展开图
正方体 展开图 各类型 记清楚
1 4 1 六变形 1 3 2 共三种
2 2 2 3 连 3 都一个 记心间
找对面 要变形 1 4 1 最清楚
（6）下列哪个图形是立方体包装盒的展开图？
（1）
（2）
（3）
（7）你能制作一个立方体纸盒吗？与同学交流。
（6）下列哪个图形是立方体包装盒的展开图？
（1）
（2）
练一练
用手势判断下面的平面图形是不是正方体的展开图？
练一练
用手势判断下面的平面图形是不是正方体的展开图？
练一练
用手势判断下面的平面图形是不是正方体的展开图？
排成“凹”字形的不行
练一练
用手势判断下面的平面图形是不是正方体的展开图？
练一练
用手势判断下面的平面图形是不是正方体的展开图？
排成“田”字形的不行
练一练
用手势判断下面的平面图形是不是正方体的展开图？
排成“T”字形的不行
练一练
用手势判断下面的平面图形是不是正方体的展开图？
排成“7”字形的不行
（1）用剪刀将一张正方形的纸片剪去一个角，还剩几个
角？剪一刀后，能使纸上剩六个角吗？试一试。
五个角
四个角
三个角
不可能使纸上剩六个角。
（2）一个立方体共有6个面，如果将这个立方体用刀切成两块，被分成的两个几何体共有几个面？如果切成10个面，怎样切？用萝卜、马铃薯或橡皮泥做一个立方体，试一试。
切断2个面，增加4个面。
切断3个面，增加5个面。
切断4个面，增加6个面。
切断5个面呢？
切断6个面呢？
1.观察右边的图形，并填空：
（1）棱是由____和_____相交而成的；
（2）顶点是由_____和_____相交而成的。
顶点
面
棱
面
面
面
棱
棱
2. 圆柱是由几个面组成的？它们分别是什么面？圆柱的
侧面和底面相交成什么线？
3.将下列第一行中的各个平面图形分别绕图中的虚线
（轴线）旋转一周，就得到第二行的立体图形。你能
把各个平面图形与旋转得到的立体图形连接起来吗？
4.一个立方体的每个面上都标了字母，右图是这个立
方体的一个展开图。请回答下列问题：
（1）如果面A是立方体朝下的面，那么哪个面朝上？
（2）如果面F朝前，面B朝左，那么哪个面朝上？
（3）如果面C朝右，面D朝后，那么哪个面朝上？
E
B
C
D
A
F