数学七年级上青岛版1.4线段的比较与作法课件1
文档属性
| 名称 | 数学七年级上青岛版1.4线段的比较与作法课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 392.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 10:56:51 | ||
图片预览









文档简介
课件33张PPT。 1、准备好课本、导学案、
练习本、双色笔
2、分析错因,自纠学案
3、标记疑难,以备讨论课前准备 第1章 基本的几何图形
1.4线段的比较与做法三案导学·初中数学七年级上(青岛版)有志者自有千计万计,无志者只感千难万难合作探究内容:
1. 学习中遇到的疑问
2.导学案“质疑探究”部分的问题
要求:
(1)人人参与,热烈讨论,大声表达自己的思想。
(2)组长控制好讨论节奏,先一对一分层讨论,再小组内集中讨论。
(3)没解决的问题组长记录好,准备质疑。
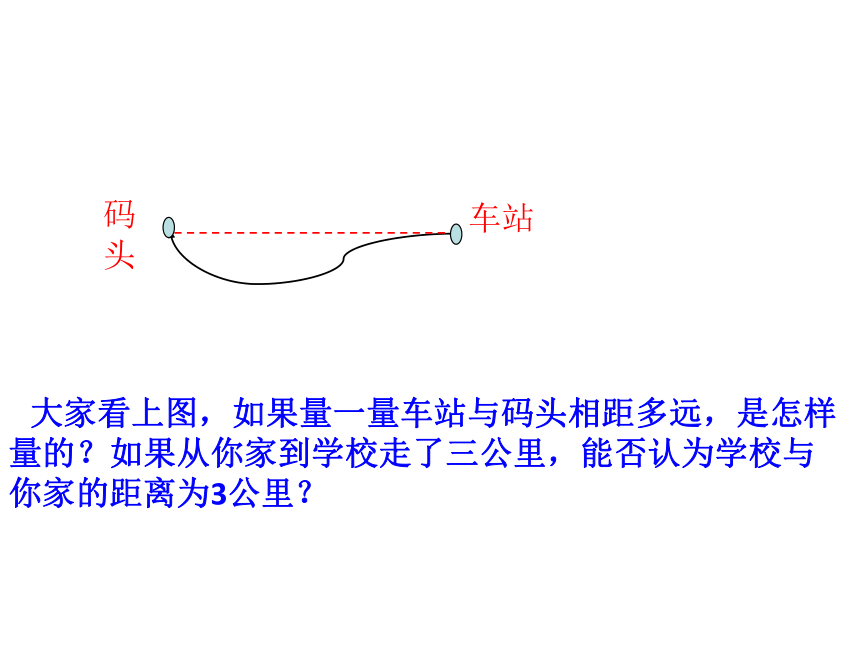
大家看上图,如果量一量车站与码头相距多远,是怎样量的?如果从你家到学校走了三公里,能否认为学校与你家的距离为3公里?
学习目标1、扎实掌握比较线段长短的方法,理解线段中点的概念,培养熟练利用数量关系表示中点的能力,会进行线段的和差及有关线段中点的计算问题,能用尺规进行作图;
2、通过学生自学、小组合作探究,掌握符号语言描述几何图形的方法;
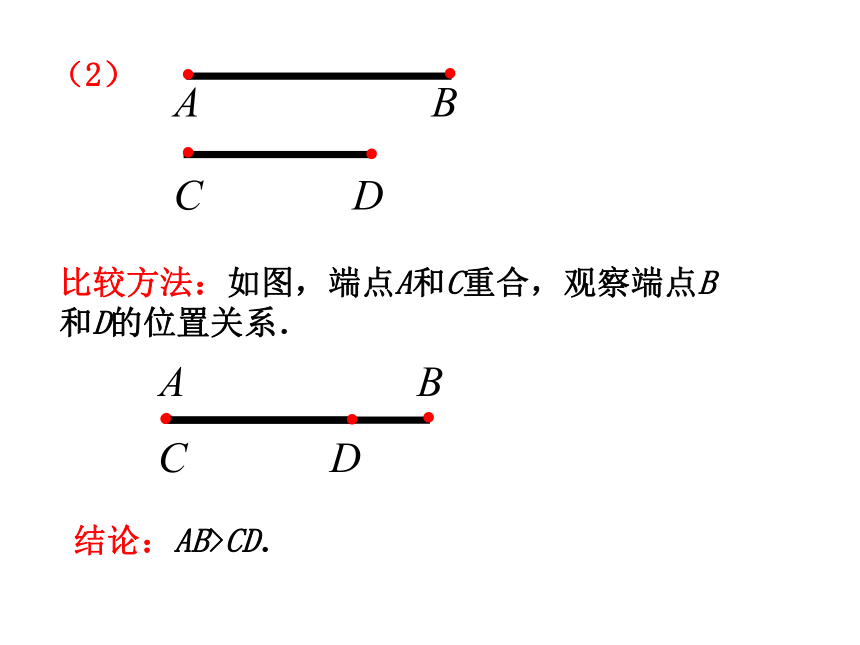
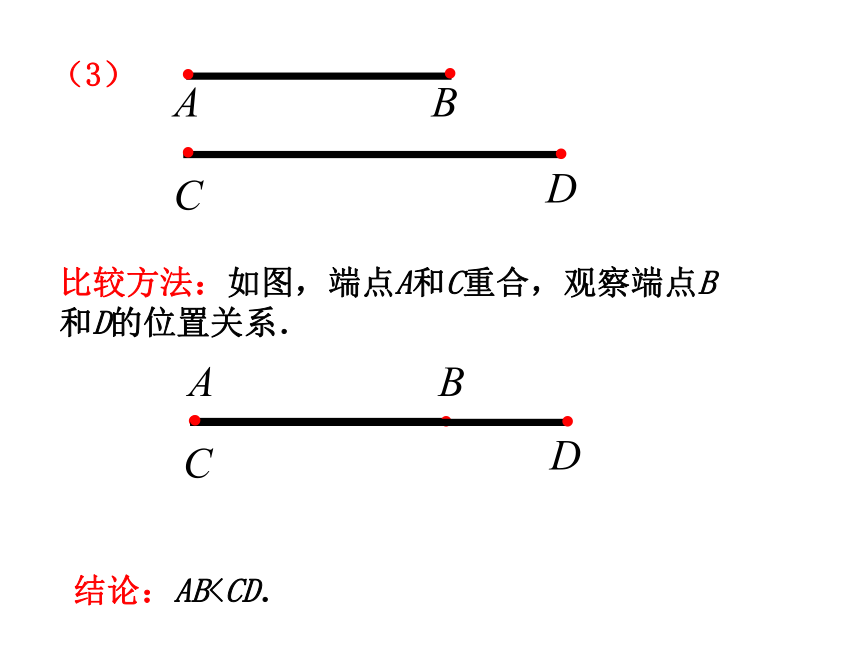
3、激情投入,全力以赴,享受学习的快乐。线段的比较1.如图,分别比较线段AB、CD的长短.比较方法:如图,端点A和C重合,观察端点B和D的位置关系.结论:AB=CD.(1)比较方法:如图,端点A和C重合,观察端点B和D的位置关系.结论:AB>CD.(2)比较方法:如图,端点A和C重合,观察端点B和D的位置关系.结论:AB于是他们决定利用今天中午休息时间见面,但两个学校之间
有四条路可走,你说他们该选择在哪条路上能较快见面?小明小聪甲乙丁丙走哪条路?两点间所有连线中,线段最短。
也可以简单说成:
两点之间线段最短。 线段的性质: 实践出真知 两点之间线段的长度,叫做这两点间的距离. 线段中点的定义: 如果点M把线段AB分成相等的两条线段AM 和BM,那么点M叫做线段AB的中点。ABMAB=2AM=2BM任意画一条线段,你能画出它的中点吗?AC=BC= AB合作探究内容:
1. 学习中遇到的疑问
2.导学案“质疑探究”部分的问题
要求:
(1)人人参与,热烈讨论,大声表达自己的思想。
(2)组长控制好讨论节奏,先一对一分层讨论,再小组内集中讨论。
(3)没解决的问题组长记录好,准备质疑。 展示点评、个个精彩展示要求:
1.展示同学积极到位,不参加展示的同学认真改正自己的错题,并写好错因,开始整理典型题目本。
2.不仅要展示题目规范的解答过程,还要用彩色笔做好总结。 展示点评、个个精彩展示要求:
1.展示同学积极到位,不参加展示的同学认真改正自己的错题,并写好错因,开始整理典型题目本。
2.不仅要展示题目规范的解答过程,还要用彩色笔做好总结。课内探究 (一)基础知识探究:探究点1.线段的基本性质
问题1.如图,从甲地到乙地有三条路。小明骑自行车从甲地到乙地走哪条路最近?
【答案】走B这条路最近
问题2.由问题1可知在两点之间的所有连线中, 最短.
【答案】线段探究点2. 两点间的距离
问题3.两点之间线段的 叫做两点间的距离.用 可以测量线段的长度.
【答案】长度. 有刻度的直尺.
【归纳总结】距离是指线段长度,是一个数值,而不是线段本身.
探究点3.线段的比较
问题4. 比较两条线段的长短的方法:
(1)“形”的叠合比较;
(2)用刻度尺度量后的比较,
【答案】叠合法、度量法【归纳总结】
叠合法 将两条线段的各一个端点对齐,看另一个端点的位置.步骤有三:
(1)将线段AB的端点A与线段CD的端点C重合.
(2)线段AB沿着线段CD的方向落下.
(3)若端点B与端点D重合,则得到线段AB等于线段CD,可以记AB=CD.
若端点B落在线段CD上,则得到线段AB小于线段CD,可以记作AB<CD.
若端点B落在线段CD外,则得到线段AB大于线段CD,可以记作AB>CD.度量法:用刻度尺分别量出线段AB和线段CD的长度,将长度进行比较.可以用推理的写法,培养推理能力.写法如下:
因为 量得AB=××cm,CD=××cm,
所以 AB=CD(或AB<CD或AB>CD).
探究点4. 线段的中点
问题4.如果点M把线段AB分成 的两条线段AM与BM,那么点M叫做线段AB的中点。
这时AM BM= AB
【答案】相等 = 【归纳总结】
线段中点的概念非常重要,应学会用符号语言表述,并会应用线段中点的性质进行有关线段的计算.(二)知识综合应用探究 探究点1. 两点间的距离
例1.如图,量得线段AB的长度为3厘米,因而A,B两点间的距离为 ,记作:
【答案】3厘米; 线段AB=3 厘米
【规律方法总结】
两点之间线段的长度叫做两点间的距离。
距离是长度,是数,不是线段,线段是一个几何图形.不能说“ A,B两点间的距离为线段AB”.探究点2. 比较两条线段的长短
例2.(1)怎样比较两个人的身高?
方法:
(2)怎样比较两条线段的长短? A_________________B
C _______________________D
方法1:
方法2:
【答案】
(1)两个人要站在一起,脚底要在一个平面上,看谁的头顶在上面,谁的身高就高。
(2)方法1:叠合法: 将两条线段的各一个端点对齐,看另一个端点的位置.步骤有三:
(1)将线段AB的端点A与线段CD的端点C重合.
(2)线段AB沿着线段CD的方向落下.
(3) 端点B落在线段CD上,则得到线段AB小于线段CD,可以记作AB<CD.
方法2:度量法: 用刻度尺分别量出线段AB和线段CD的长度,将长度进行比较.可以用推理的写法,培养推理能力.写法如下:
因为 量得AB=5cm,CD=7cm,
所以 AB<CD探究点3. 线段的有关计算
例3. 如图1,已知AC=8cm,BC=4cm,D是BC的中点,E是AB的中点,求AD和EC的长。
【解题指导】利用线段中点的概念可求出BD和AE的长,结合图形,利用AD=AB-DB,EC=AC-AE即可求出结果。【拓展提升】如图2,已知线段AB=16cm,C是AB上一点,
D是AC的中点,E是BC的中点,求线段DE的长。
【规律方法总结】本题运用了数形结合和整体代换的思想
方法,解题中注意线段中点性质的应用,总结升华 本节主要学习了比较线段长短的两种方法,线段中点的概念、线段的基本性质和两点间距离;同学们应掌握线段的和差及有关线段中点的计算,培养逻辑推理能力,掌握数形结合,整体代换,分类讨论的数学思想方法. 整理巩固要求:整理巩固探究问题
落实基础知识
完成知识结构图当堂检测 【答案】BC CD,AB BC,AC .2. 己知AB=6cm,P点是到A、B两点等距离的点,则AP长为( )
A、3cm B、4cm C、5cm D、不能确定
【答案】A3、如图,在直线AB上找出一点C,使AC=2CB,则C点应在( )
A、点A、B之间 B、点A的左边
C、点B的左边 D、点A、B之间或点B的右边
【答案】D课堂评价学科班长:1.回扣目标 总结收获
2.评出优秀小组和个人
课后完成训练学案并整理巩固thanks
练习本、双色笔
2、分析错因,自纠学案
3、标记疑难,以备讨论课前准备 第1章 基本的几何图形
1.4线段的比较与做法三案导学·初中数学七年级上(青岛版)有志者自有千计万计,无志者只感千难万难合作探究内容:
1. 学习中遇到的疑问
2.导学案“质疑探究”部分的问题
要求:
(1)人人参与,热烈讨论,大声表达自己的思想。
(2)组长控制好讨论节奏,先一对一分层讨论,再小组内集中讨论。
(3)没解决的问题组长记录好,准备质疑。
大家看上图,如果量一量车站与码头相距多远,是怎样量的?如果从你家到学校走了三公里,能否认为学校与你家的距离为3公里?
学习目标1、扎实掌握比较线段长短的方法,理解线段中点的概念,培养熟练利用数量关系表示中点的能力,会进行线段的和差及有关线段中点的计算问题,能用尺规进行作图;
2、通过学生自学、小组合作探究,掌握符号语言描述几何图形的方法;
3、激情投入,全力以赴,享受学习的快乐。线段的比较1.如图,分别比较线段AB、CD的长短.比较方法:如图,端点A和C重合,观察端点B和D的位置关系.结论:AB=CD.(1)比较方法:如图,端点A和C重合,观察端点B和D的位置关系.结论:AB>CD.(2)比较方法:如图,端点A和C重合,观察端点B和D的位置关系.结论:AB
有四条路可走,你说他们该选择在哪条路上能较快见面?小明小聪甲乙丁丙走哪条路?两点间所有连线中,线段最短。
也可以简单说成:
两点之间线段最短。 线段的性质: 实践出真知 两点之间线段的长度,叫做这两点间的距离. 线段中点的定义: 如果点M把线段AB分成相等的两条线段AM 和BM,那么点M叫做线段AB的中点。ABMAB=2AM=2BM任意画一条线段,你能画出它的中点吗?AC=BC= AB合作探究内容:
1. 学习中遇到的疑问
2.导学案“质疑探究”部分的问题
要求:
(1)人人参与,热烈讨论,大声表达自己的思想。
(2)组长控制好讨论节奏,先一对一分层讨论,再小组内集中讨论。
(3)没解决的问题组长记录好,准备质疑。 展示点评、个个精彩展示要求:
1.展示同学积极到位,不参加展示的同学认真改正自己的错题,并写好错因,开始整理典型题目本。
2.不仅要展示题目规范的解答过程,还要用彩色笔做好总结。 展示点评、个个精彩展示要求:
1.展示同学积极到位,不参加展示的同学认真改正自己的错题,并写好错因,开始整理典型题目本。
2.不仅要展示题目规范的解答过程,还要用彩色笔做好总结。课内探究 (一)基础知识探究:探究点1.线段的基本性质
问题1.如图,从甲地到乙地有三条路。小明骑自行车从甲地到乙地走哪条路最近?
【答案】走B这条路最近
问题2.由问题1可知在两点之间的所有连线中, 最短.
【答案】线段探究点2. 两点间的距离
问题3.两点之间线段的 叫做两点间的距离.用 可以测量线段的长度.
【答案】长度. 有刻度的直尺.
【归纳总结】距离是指线段长度,是一个数值,而不是线段本身.
探究点3.线段的比较
问题4. 比较两条线段的长短的方法:
(1)“形”的叠合比较;
(2)用刻度尺度量后的比较,
【答案】叠合法、度量法【归纳总结】
叠合法 将两条线段的各一个端点对齐,看另一个端点的位置.步骤有三:
(1)将线段AB的端点A与线段CD的端点C重合.
(2)线段AB沿着线段CD的方向落下.
(3)若端点B与端点D重合,则得到线段AB等于线段CD,可以记AB=CD.
若端点B落在线段CD上,则得到线段AB小于线段CD,可以记作AB<CD.
若端点B落在线段CD外,则得到线段AB大于线段CD,可以记作AB>CD.度量法:用刻度尺分别量出线段AB和线段CD的长度,将长度进行比较.可以用推理的写法,培养推理能力.写法如下:
因为 量得AB=××cm,CD=××cm,
所以 AB=CD(或AB<CD或AB>CD).
探究点4. 线段的中点
问题4.如果点M把线段AB分成 的两条线段AM与BM,那么点M叫做线段AB的中点。
这时AM BM= AB
【答案】相等 = 【归纳总结】
线段中点的概念非常重要,应学会用符号语言表述,并会应用线段中点的性质进行有关线段的计算.(二)知识综合应用探究 探究点1. 两点间的距离
例1.如图,量得线段AB的长度为3厘米,因而A,B两点间的距离为 ,记作:
【答案】3厘米; 线段AB=3 厘米
【规律方法总结】
两点之间线段的长度叫做两点间的距离。
距离是长度,是数,不是线段,线段是一个几何图形.不能说“ A,B两点间的距离为线段AB”.探究点2. 比较两条线段的长短
例2.(1)怎样比较两个人的身高?
方法:
(2)怎样比较两条线段的长短? A_________________B
C _______________________D
方法1:
方法2:
【答案】
(1)两个人要站在一起,脚底要在一个平面上,看谁的头顶在上面,谁的身高就高。
(2)方法1:叠合法: 将两条线段的各一个端点对齐,看另一个端点的位置.步骤有三:
(1)将线段AB的端点A与线段CD的端点C重合.
(2)线段AB沿着线段CD的方向落下.
(3) 端点B落在线段CD上,则得到线段AB小于线段CD,可以记作AB<CD.
方法2:度量法: 用刻度尺分别量出线段AB和线段CD的长度,将长度进行比较.可以用推理的写法,培养推理能力.写法如下:
因为 量得AB=5cm,CD=7cm,
所以 AB<CD探究点3. 线段的有关计算
例3. 如图1,已知AC=8cm,BC=4cm,D是BC的中点,E是AB的中点,求AD和EC的长。
【解题指导】利用线段中点的概念可求出BD和AE的长,结合图形,利用AD=AB-DB,EC=AC-AE即可求出结果。【拓展提升】如图2,已知线段AB=16cm,C是AB上一点,
D是AC的中点,E是BC的中点,求线段DE的长。
【规律方法总结】本题运用了数形结合和整体代换的思想
方法,解题中注意线段中点性质的应用,总结升华 本节主要学习了比较线段长短的两种方法,线段中点的概念、线段的基本性质和两点间距离;同学们应掌握线段的和差及有关线段中点的计算,培养逻辑推理能力,掌握数形结合,整体代换,分类讨论的数学思想方法. 整理巩固要求:整理巩固探究问题
落实基础知识
完成知识结构图当堂检测 【答案】BC CD,AB BC,AC .2. 己知AB=6cm,P点是到A、B两点等距离的点,则AP长为( )
A、3cm B、4cm C、5cm D、不能确定
【答案】A3、如图,在直线AB上找出一点C,使AC=2CB,则C点应在( )
A、点A、B之间 B、点A的左边
C、点B的左边 D、点A、B之间或点B的右边
【答案】D课堂评价学科班长:1.回扣目标 总结收获
2.评出优秀小组和个人
课后完成训练学案并整理巩固thanks
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
