数学七年级上青岛版2.3相反数与绝对值课件4
文档属性
| 名称 | 数学七年级上青岛版2.3相反数与绝对值课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-01 00:00:00 | ||
图片预览




文档简介
课件26张PPT。2.3 绝对值与相反数
复习:1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
2、数轴的三要素原点、正方向、单位长度3、画出数轴、并用数轴上的点表示下列各数:
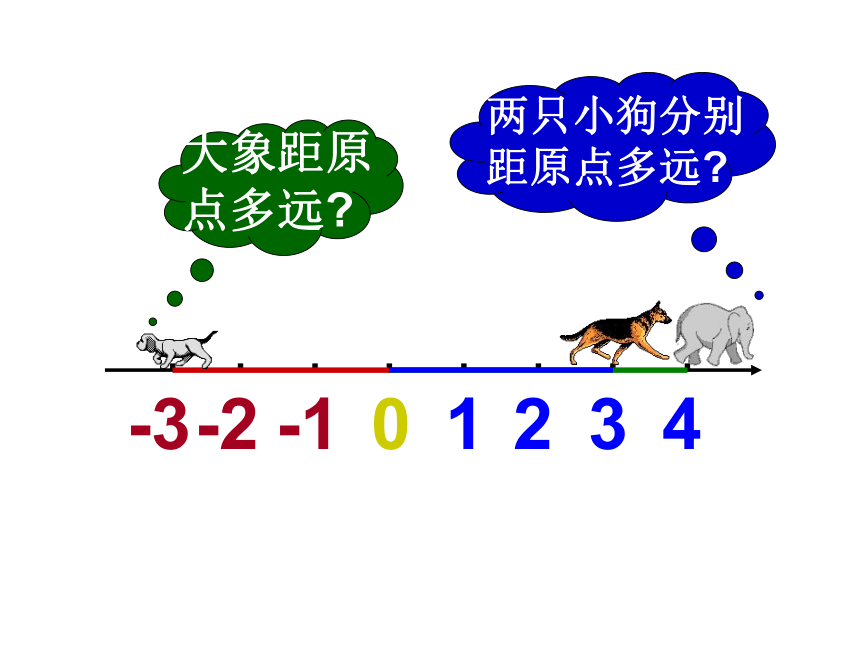
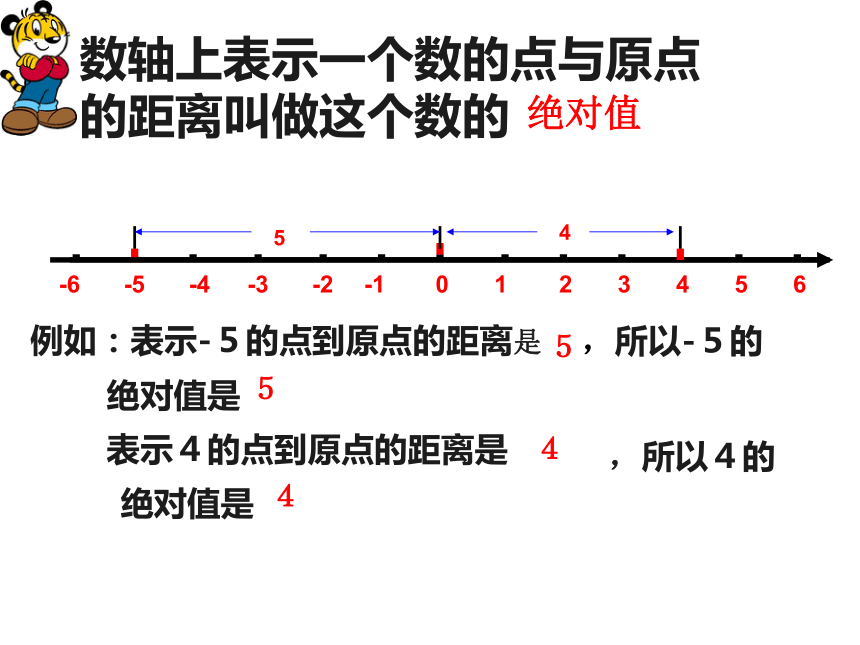
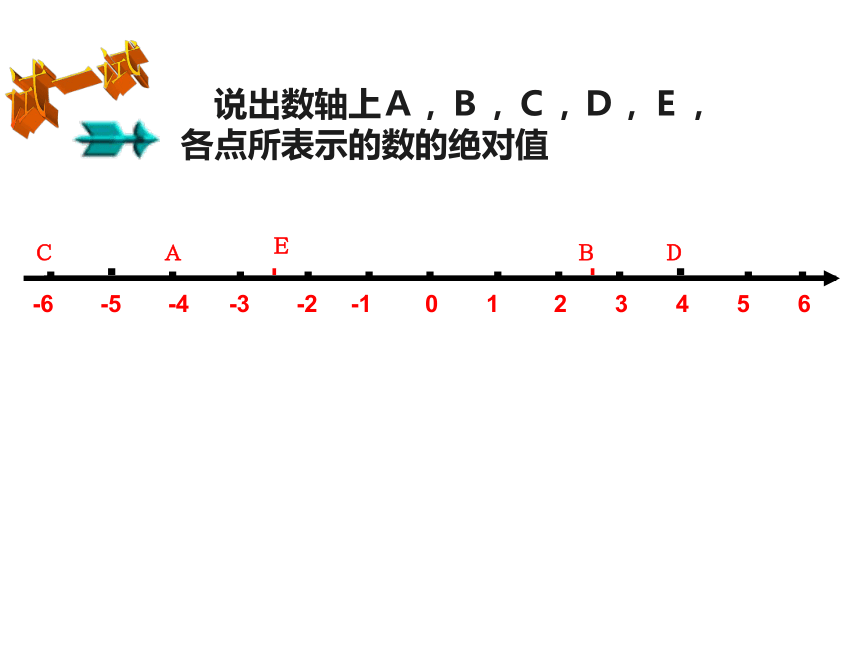
-1.5 , 0 , -6 ,2 , +6 ,-3 ,3做一做解:01234-1-2-3引入绝对值数轴上表示一个数的点与原点的距离叫做这个数的例如:表示-5的点到原点的距离是,所以-5的5绝对值是5,所以4的4绝对值是4表示4的点到原点的距离是绝对值试一试 说出数轴上A,B,C,D,E,各点所表示的数的绝对值绝对值符号的表示方法绝对值用“ ”表示,如4的绝对值记作-3.5的绝对值记作 练习:
1.表示+7的点与原点的距离是 ,即+7的绝值是 ,记作 ;
2.表示2.8的点与原点的距离是 ,即2.8的绝对值是 ,记作 ;
3.表示0的点与原点的距离是 ,即0的绝对值是 ,记作 ;
4. 表示-5的点与原点的距离是 ,即-5的绝对值是 ,记作 ;
你能求出它们的值吗?=3=6=0=1.5=0.4=2 试一试例题例1 求下列各数的绝对值:
-21, , 0 , -7.8 解:一个数的绝对值与这个数有什么关系?例如:|3|=3,|+7|=7正数的绝对值是它本身例如:|-3|=3,|-2.3|=2.3 负数的绝对值是它的相反数0的绝对值是0议一议 因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0 议一议 (1)绝对值是7的数有几个?各是什么?有没有绝对值是-2的数
(2)绝对值是0的数有几个?各是什么
(3)绝对值小于5的整数一共有多少个?请写 出,并在数轴上表示出来。 例题填空1、绝对值是10的数有( )
+10和-10|+15|=
|–4|=
| 0 |=
| 4 |=+15+4042.判断: (1)绝对值都是正数。 ( ) (2)互为相反数的绝对值相等 ×√正数或零(3.)一个数的绝对值是它本身,那么这个数一定是__________.4.绝对值小于5的整数有___个,分别是_______________.
(2)已知 ,那么 拓展和延伸2、绝对值小于5的整数有 个,它们分别是 . 1、大于-3而小于5的整数有 个,它们分别是 . 3、绝对值不大于3的整数有 个,它们分别是 . 你发现了什么?求下列各组数的绝对值:(1)4,-4; (2) 0.8,-0.8;(3)想一想互为相反数的两个数的绝对值有什么关系? 解:(1)|4|=4 |-4|=4(2)|0.8|=0.8 |-0.8|=0.8相等挑战自我01做一做 ( 1 )在数轴上表示下列各数,并比较它们的大小:
- 1.5 , - 3 , - 1 , - 5
( 2 ) 求出(1)中各数的绝对值,并比较它们的大小
( 3 )你发现了什么?解:(1) - 5 < - 3 <- 1.5 < - 1(2)| -1.5 | = 1.5 ; | - 3 | = 3;
| -1 | = 1 ; | - 5 | = 5.
(3)由以上知:两个负数比较大小,绝对值大的反而小1 < 1.5 <3 <5解法一(利用绝对值比较两个负数的大小)解: (1)| -1| = 1,| -5 | = 5 ,1﹤5,
所以 - 1> - 5例题例2. 比较下列每组数的大小
(1) -1和 – 5; (2)- 和- 2.7(2)因为| - | = ,|- 2.7| =2.7,
﹤2.7,所以 - ﹥-2.7解法二 (利用数轴比较两个负数的大小)
(2)解:(1)因为- 2.7在 - 的左边,所以- 2.7﹤-因为- 5在 –1左边,所以 - 5﹤ - 12、(1)有没有最小的正数和最大的正数?(2)有没有最小的负数和最大的负数?(5)有没有绝对值最小的数和绝对值最大的数?(3)有没有最小的正整数和最大的正整数?(4)有没有最小的负整数和最大的负整数?最小的正整数是1,最大的负整数是-1,
绝对值最小的数是0.●●●没有没有没有没有有1没有没有有-1有0没有3、(1)-1与0之间还有负数吗? 与0之间呢?
如有,请举例.
(2)-3与-1之间有负整数吗?-2与2之间有哪些整数?
(3)有比-1大的整数吗?
(4)写出3个小于-100并且大于-103的数.有 例:-0.1 有 例: -2有 例:0,3例:-101 -101.5 -1021,0,-1
复习:1、什么是数轴?
数轴是规定了原点、正方向、单位长度的直线
2、数轴的三要素原点、正方向、单位长度3、画出数轴、并用数轴上的点表示下列各数:
-1.5 , 0 , -6 ,2 , +6 ,-3 ,3做一做解:01234-1-2-3引入绝对值数轴上表示一个数的点与原点的距离叫做这个数的例如:表示-5的点到原点的距离是,所以-5的5绝对值是5,所以4的4绝对值是4表示4的点到原点的距离是绝对值试一试 说出数轴上A,B,C,D,E,各点所表示的数的绝对值绝对值符号的表示方法绝对值用“ ”表示,如4的绝对值记作-3.5的绝对值记作 练习:
1.表示+7的点与原点的距离是 ,即+7的绝值是 ,记作 ;
2.表示2.8的点与原点的距离是 ,即2.8的绝对值是 ,记作 ;
3.表示0的点与原点的距离是 ,即0的绝对值是 ,记作 ;
4. 表示-5的点与原点的距离是 ,即-5的绝对值是 ,记作 ;
你能求出它们的值吗?=3=6=0=1.5=0.4=2 试一试例题例1 求下列各数的绝对值:
-21, , 0 , -7.8 解:一个数的绝对值与这个数有什么关系?例如:|3|=3,|+7|=7正数的绝对值是它本身例如:|-3|=3,|-2.3|=2.3 负数的绝对值是它的相反数0的绝对值是0议一议 因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0 议一议 (1)绝对值是7的数有几个?各是什么?有没有绝对值是-2的数
(2)绝对值是0的数有几个?各是什么
(3)绝对值小于5的整数一共有多少个?请写 出,并在数轴上表示出来。 例题填空1、绝对值是10的数有( )
+10和-10|+15|=
|–4|=
| 0 |=
| 4 |=+15+4042.判断: (1)绝对值都是正数。 ( ) (2)互为相反数的绝对值相等 ×√正数或零(3.)一个数的绝对值是它本身,那么这个数一定是__________.4.绝对值小于5的整数有___个,分别是_______________.
(2)已知 ,那么 拓展和延伸2、绝对值小于5的整数有 个,它们分别是 . 1、大于-3而小于5的整数有 个,它们分别是 . 3、绝对值不大于3的整数有 个,它们分别是 . 你发现了什么?求下列各组数的绝对值:(1)4,-4; (2) 0.8,-0.8;(3)想一想互为相反数的两个数的绝对值有什么关系? 解:(1)|4|=4 |-4|=4(2)|0.8|=0.8 |-0.8|=0.8相等挑战自我01做一做 ( 1 )在数轴上表示下列各数,并比较它们的大小:
- 1.5 , - 3 , - 1 , - 5
( 2 ) 求出(1)中各数的绝对值,并比较它们的大小
( 3 )你发现了什么?解:(1) - 5 < - 3 <- 1.5 < - 1(2)| -1.5 | = 1.5 ; | - 3 | = 3;
| -1 | = 1 ; | - 5 | = 5.
(3)由以上知:两个负数比较大小,绝对值大的反而小1 < 1.5 <3 <5解法一(利用绝对值比较两个负数的大小)解: (1)| -1| = 1,| -5 | = 5 ,1﹤5,
所以 - 1> - 5例题例2. 比较下列每组数的大小
(1) -1和 – 5; (2)- 和- 2.7(2)因为| - | = ,|- 2.7| =2.7,
﹤2.7,所以 - ﹥-2.7解法二 (利用数轴比较两个负数的大小)
(2)解:(1)因为- 2.7在 - 的左边,所以- 2.7﹤-因为- 5在 –1左边,所以 - 5﹤ - 12、(1)有没有最小的正数和最大的正数?(2)有没有最小的负数和最大的负数?(5)有没有绝对值最小的数和绝对值最大的数?(3)有没有最小的正整数和最大的正整数?(4)有没有最小的负整数和最大的负整数?最小的正整数是1,最大的负整数是-1,
绝对值最小的数是0.●●●没有没有没有没有有1没有没有有-1有0没有3、(1)-1与0之间还有负数吗? 与0之间呢?
如有,请举例.
(2)-3与-1之间有负整数吗?-2与2之间有哪些整数?
(3)有比-1大的整数吗?
(4)写出3个小于-100并且大于-103的数.有 例:-0.1 有 例: -2有 例:0,3例:-101 -101.5 -1021,0,-1
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
