单项式乘多项式

课件28张PPT。单项式乘多项式1、同底数幂的乘法:2、幂的乘方： (m,n均为正整数）(m,n均为正整数）3、积的乘方：(n为正整数）?单项式与单项式相乘：你还记得吗？把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式快速抢答！1.判断正误（如果不对应如何改正?)
（1）4a3·2a2=8a6 （ ）
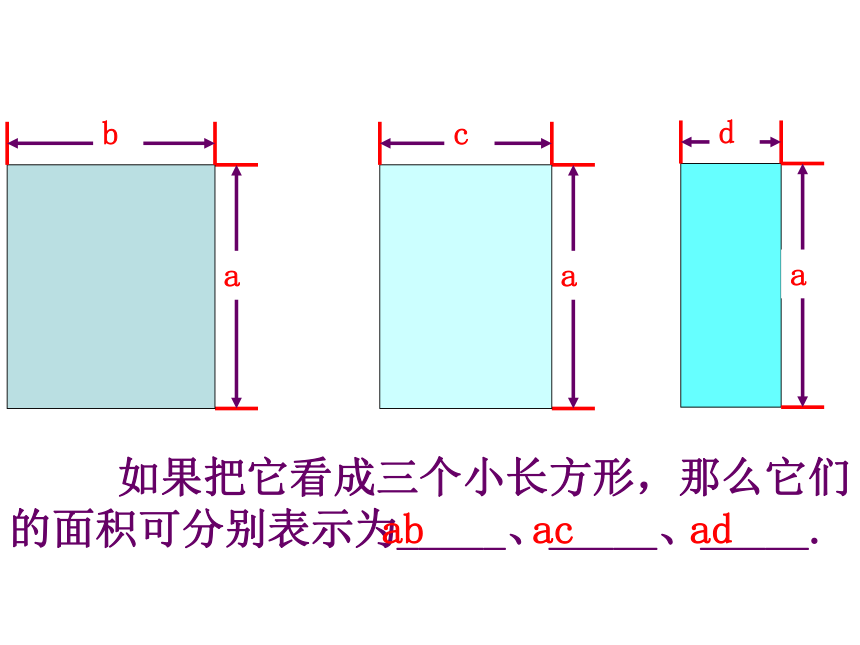
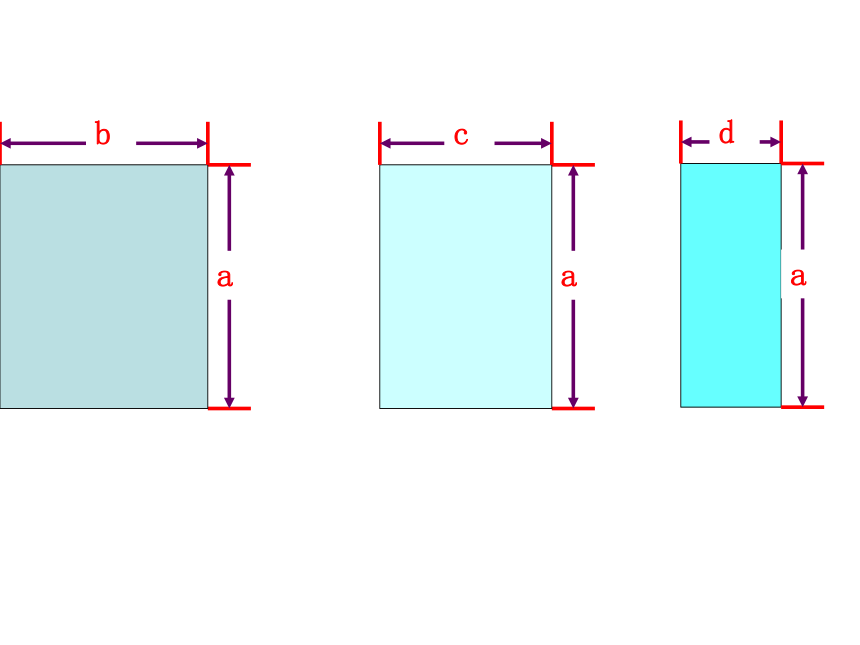
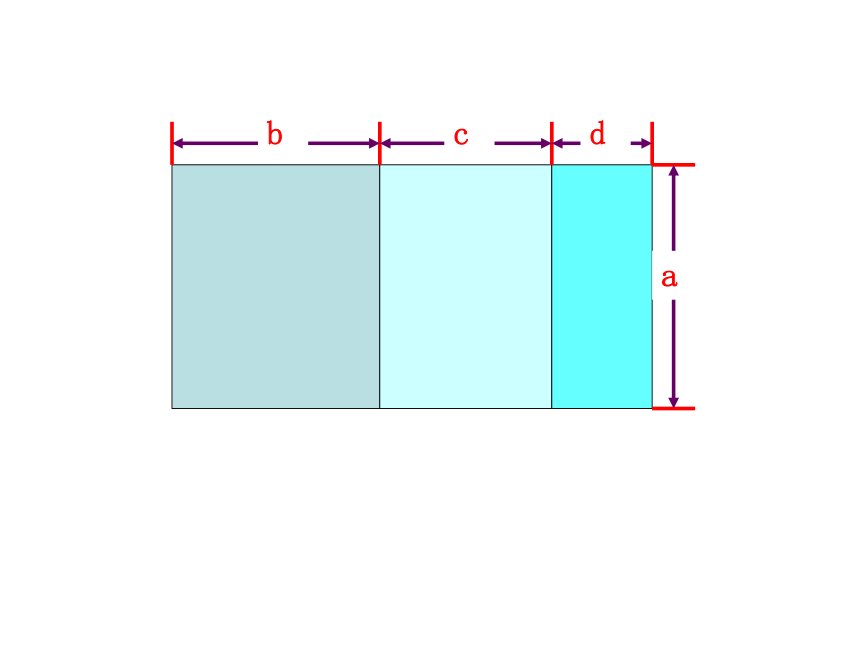
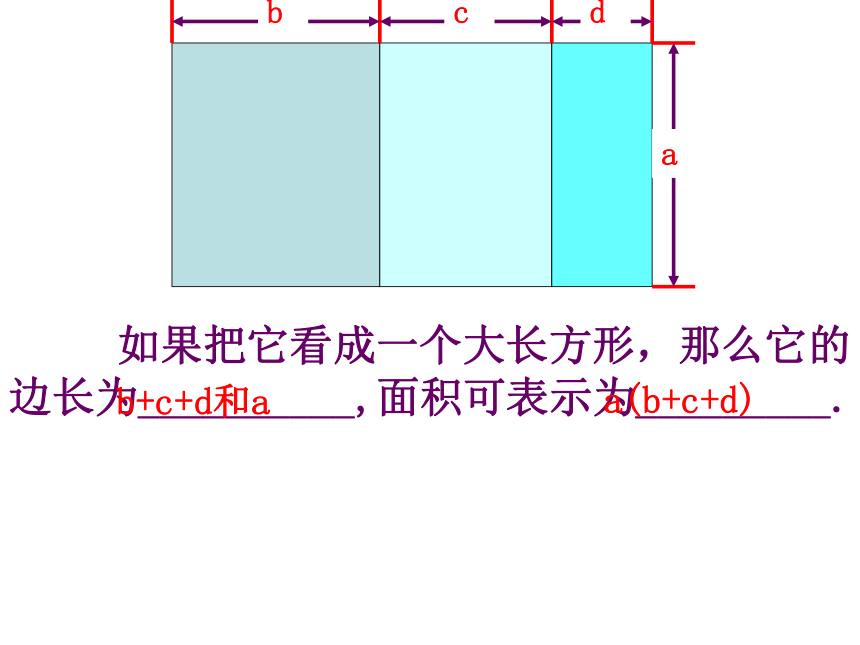
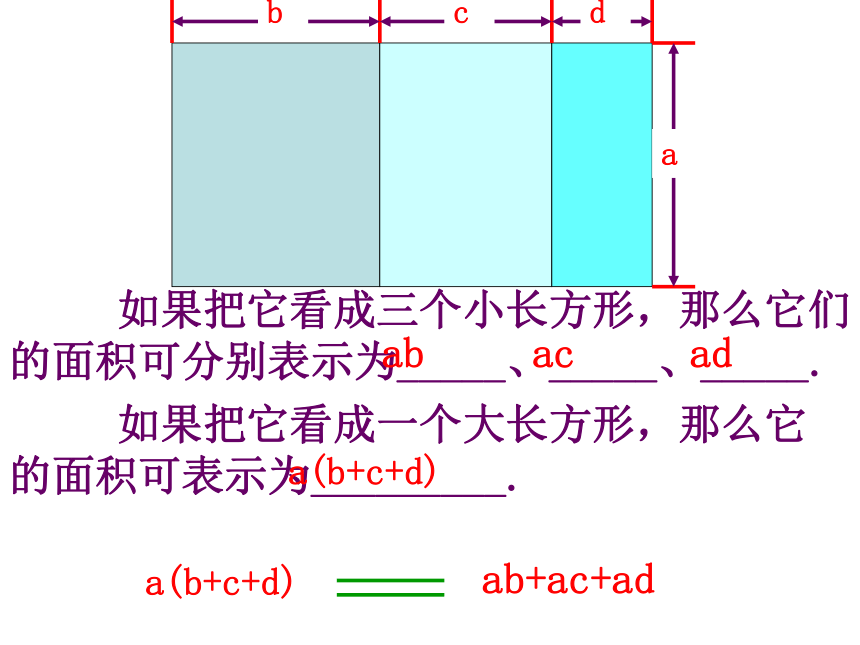
（2）（ ） （3） （ ） 如果把它看成三个小长方形，那么它们的面积可分别表示为_____、_____、_____. abadac 如果把它看成一个大长方形，那么它的边长为__________,面积可表示为_________. b+c+d和aa(b+c+d) 如果把它看成三个小长方形，那么它们的面积可分别表示为_____、_____、_____. 如果把它看成一个大长方形，那么它的面积可表示为_________. a(b+c+d)ab+ac+ada(b+c+d)a(b+c+d)ac+adab+根据乘法的分配律 单项式与多项式相乘，就是依据乘法分配律，用单项式乘多项式的每一项，再把所得的积相加.单项式乘多项式的运算法则 单项式与多项式相乘，就是依据乘法分配律，用单项式乘多项式的每一项，再把所得的积相加.例1 计算：
⑴ (-3a) ·(-2a2-3a-2)解：(-3a) ·(-2a2-3a-2)
＝(-3a) ·(-2a2)+(-3a) ·(-3a)+(-3a) ·(-2)
＝6a3+9a2+6a乘法分配率单项式乘单项式运算法则例2 计算：
( -2ab )3 ( 5a2b – 0.5ab2+0.25b3 )解：原式=(-8a 3 b 3) ( 5a2b – 0.5ab2+0.25b3 ) =(-8a 3 b 3) ·（5a2b） +(-8a 3 b 3) ·(- 0.5ab2 ） +(-8a 3 b 3) ·（0.25b3 ） = - 40a 5b4+4a4b 5– 2a3b6说明：先进行乘方运算，
再进行单项式与多项式的乘法运算。例3 计算：x [ x（x - 1）- 1]解法一： x [ x（x - 1）- 1] 解法二： x [ x（x - 1）- 1]= x [（x 2– x）- 1]= x （x 2– x – 1）说明：先去小括号，再去中括号。= x3 – x2 - x= x3 – x2 - x= x ? x（x - 1）- x= x2（x - 1）- x说明：先把x（x – 1）看成整体，按乘法对加法的分配律去掉中括号，再去掉小括号。例4 解方程
7x -（x – 3）x – 3x（2 – x）=（2x + 1）x + 6解：去括号，得
7x – x 2+ 3x – 6x + 3x 2 = 2x 2 + x + 6移项，得
7x – x 2+ 3x – 6x + 3x 2 - 2x 2 - x = 6合并同类项，得 3x = 6系数化为1，得 x = 2 例6 求值：
yn(yn + 9y - 12) – 3(3yn+1 - 4yn)，
其中y= - 3，n=2.解： yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3，n=2时，原式=（- 3）4=81求值问题，方法不是惟一的，可以直接把字母的值代入原式，但计算繁琐易出错，应先化简，再代入求值，就显得非常简捷。计算：
⑴ a (2a-3) ⑵ a2 (1-3a) ⑶ 3x(x2-2x-1) ⑷ -2x2y(3x2-2x-3) (5) (2x2-3xy+4y2)(-2xy)例2：如图：一块长方形地用来建造住宅、广场、商厦，求这块地的面积.解：长方形的长为(3a+2b)+(2a-b),宽为4a,这块地的面积为：4a[(3a+2b)+(2a-b)]
＝4a(5a+b)
＝4a·5a+4a·b
=20a2+4ab
答：这块地的面积为20a2+4ab.计算：
⑴ 3x(x2-2x-1)-2x2(x-3) ⑵ -6xy(x2-2xy-y2)+3xy(2x2-4xy+y2) ⑶ x2-2x[2x2-3(x2-2x-3)] ⑷ 2a(a2-3a-4)-a(2a2+6a-1)解方程：
⑴ 2x(x-1)-x(3x+2)=-x(x+2)-12 ⑵ x2(3x+5)＋5=x(-x2+4x2+5x)+x已知：xy2=-6,求-xy(x3y7-3x2y5-y)1.判断题：
（1）单项式乘以单项式，结果一定是单项式 （ ）
（2）两个单项式相乘，积的次数是两个单项式次数的积 （ ）
（3）单项式与多项式相乘的结果一定是一个多项式，其项数与因式中多项式的项数相同 （ ）计算：3x3x2x2x2x+5求图中物体的体积.若a=2,b=5,m=3,n=4,分别求下列各式的值：
(a+b)(m+n)
a(m+n)+b(m+n)
am+an+bm+bn
从上面的计算中你发现什么？再找一组看看你能从图中得到这个结论吗？课时小结： 1、单项式与多项式相乘的实质是利用分配律把单项式 乘以多项式转化为单项式乘法 2.单项式与多项式相乘时，分三个阶段：
①按分配律把乘积写成单项式与单项式乘积的代数和的形式；
②按照单项式的乘法法则运算。
③再把所得的积相加.1.计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时，同号相乘得正，异号相乘得负。 2.不要出现漏乘现象。3.运算要有顺序：先乘方，再乘除，最后加减。4.对于混合运算，注意最后应合并同类项。四点注意：这节课，我的收获是---小结与回顾