4.1.2函数的表示法课件

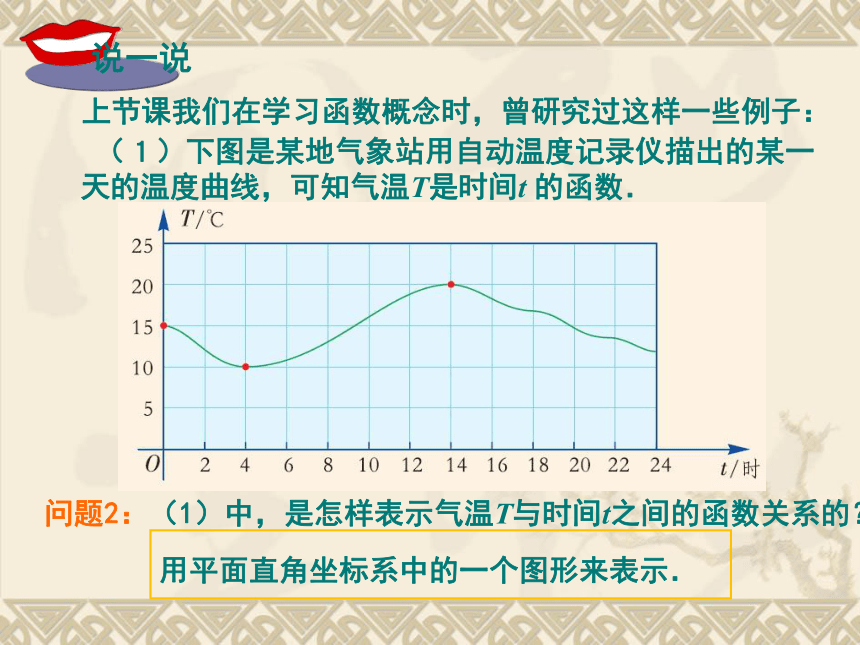
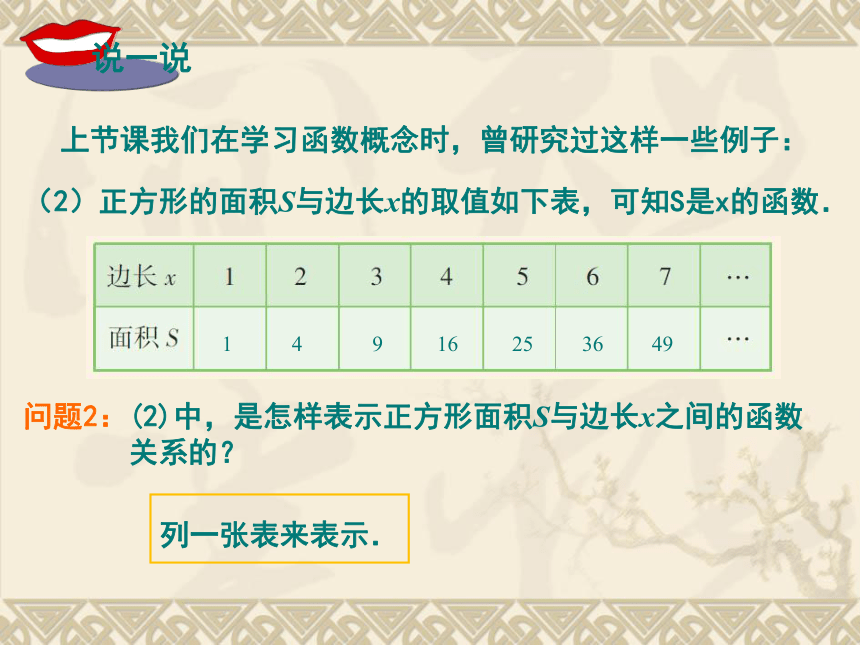
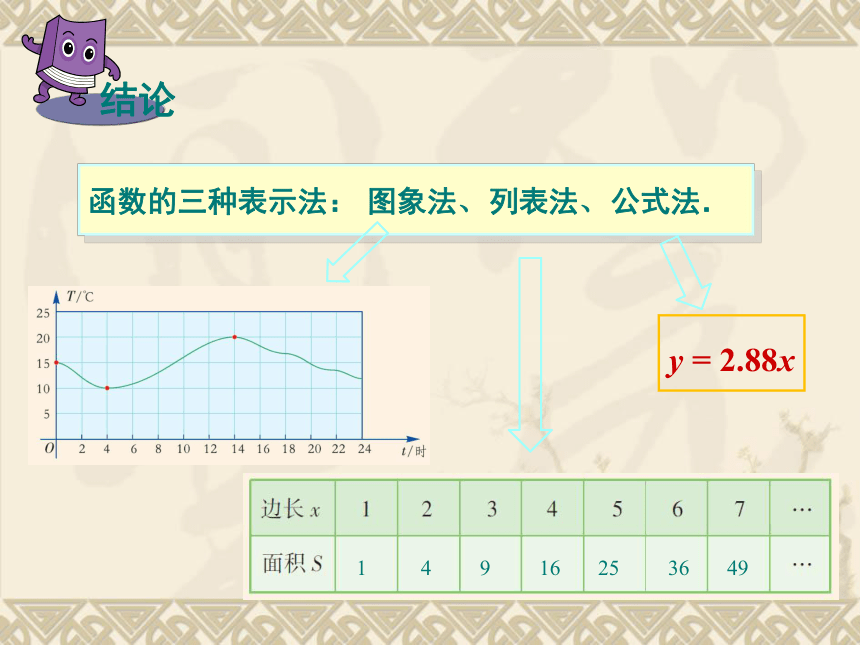
课件36张PPT。 函数和它的表示法4.14.1.2函数的表示法返回 问题1：上节课我们学习了函数的概念，你能说出什么叫做函数吗？一般地， 如果变量y随着变量x而变化， 并且对于x取的每一个值， y都有唯一的一个值与它对应， 那么称y是x的函数．问题2：（1）中，是怎样表示气温T与时间t之间的函数关系的？用平面直角坐标系中的一个图形来表示． （１）下图是某地气象站用自动温度记录仪描出的某一天的温度曲线，可知气温T是时间t 的函数． 上节课我们在学习函数概念时，曾研究过这样一些例子： （2）正方形的面积S与边长x的取值如下表，可知S是x的函数．问题2：(2)中，是怎样表示正方形面积S与边长x之间的函数
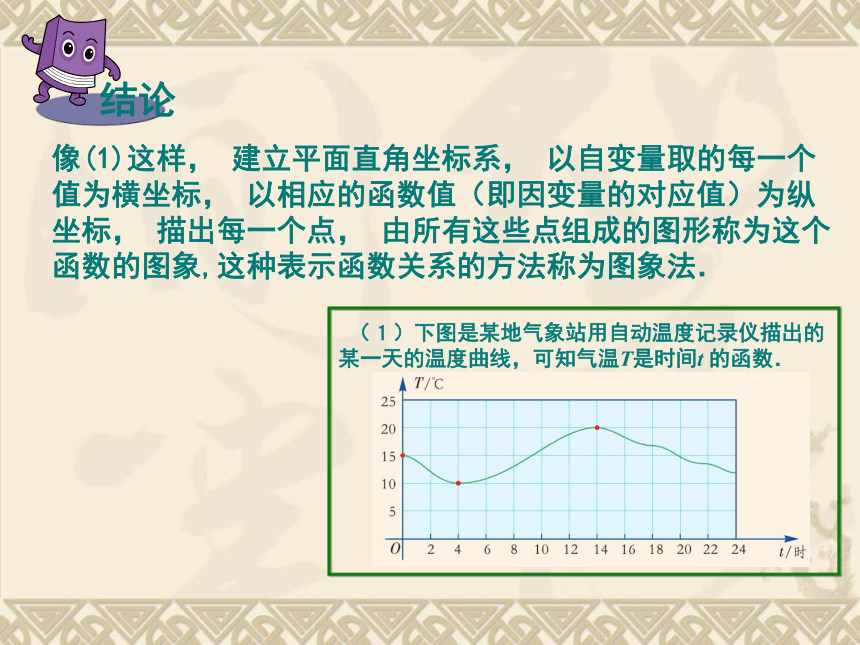
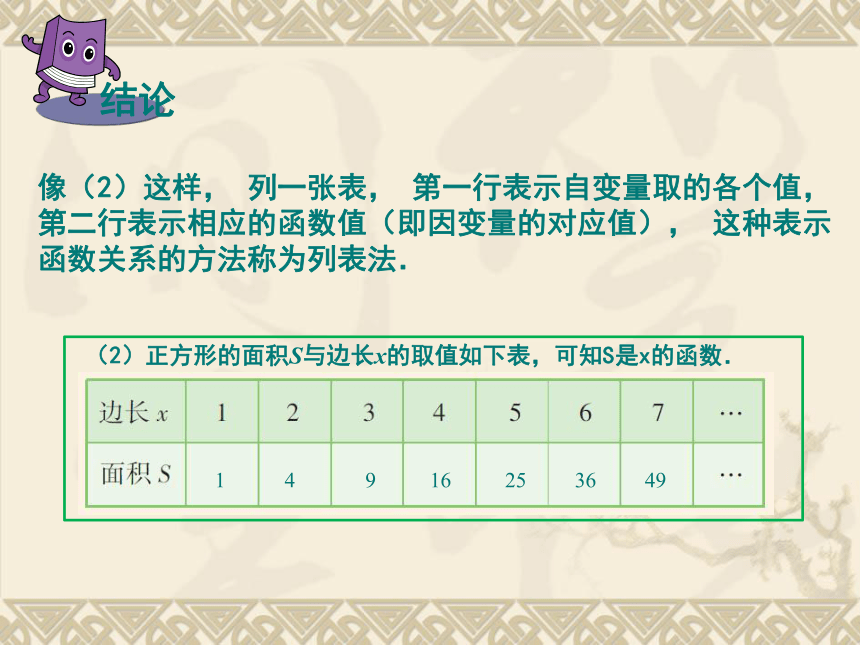
关系的？ 上节课我们在学习函数概念时，曾研究过这样一些例子：列一张表来表示． 1 4 9 16 25 36 49 （3）某城市居民用的天然气， １m3收费2.88元， 使用x （m3） 天然气应缴纳的费用y（元）为y = 2.88x．可知y是x 的函数．问题2：(3)中，是怎样表示缴纳的天然气费y与所用天然气的体积x的函数关系的？用一个式子y＝2.88x来表示． 上节课我们在学习函数概念时，曾研究过这样一些例子：像(1)这样， 建立平面直角坐标系， 以自变量取的每一个值为横坐标， 以相应的函数值（即因变量的对应值）为纵坐标， 描出每一个点， 由所有这些点组成的图形称为这个函数的图象,这种表示函数关系的方法称为图象法． （2）正方形的面积S与边长x的取值如下表，可知S是x的函数．像（2）这样， 列一张表， 第一行表示自变量取的各个值， 第二行表示相应的函数值（即因变量的对应值）， 这种表示函数关系的方法称为列表法．
像（3）这样，用式子表示函数关系的方法称为公式法， 这样的式子称为函数的表达式．（3）某城市居民用的天然气， １m3收费2.88元， 使用x （m3） 天然气应缴纳的费用y（元）为
y = 2.88x．可知y是x的函数．
函数的三种表示法：y = 2.88x图象法、列表法、公式法． 1 4 9 16 25 36 49 问题3：你能谈谈用图象法、列表法、公式法表示函数关系时各自的优点吗？用图象法表示函数关系，可以直观地看出因变量如何随着自变量而变化；用列表法表示函数关系，可以很清楚地看出自变量取的值与因变量的对应值；用公式法表示函数关系，可以方便地计算函数值．问题4：你能举出一些用图象法、列表法、表达式表示函数关系的例子吗？　举例：（1）某班8名学生的身高y（单位：厘米）与学号x的函数关系如下表：如下表：（2）一支铅笔2元，买x支铅笔所需的费用为y元，则y与x的函数关系可表示为：y=2x(x为正整数）.问题4：你能举出一些用图像法、列表法、表达式表示函数关系的例子吗？　举例：（3）下图是某市3月1日至14日的空气质量指数趋势图，空气质量指数y是日期x的函数.问题5：是不是所有的函数都可以用函数表达式的形式表示出来呢?　举例：S=x2这个函数可以用函数表达式的形式表示.问题5：是不是所有的函数都可以用函数表达式的形式表示出来呢?　举例：这些函数不能用函数表达式的形式表示请建立平面直角坐标系，任意画出一个函数图象
（1）请判断你周围的同学画的图象是不是函数图象？（2）下面的图象中，y是x的函数吗？（3）怎么判断一个图象是否是函数图象？ １．用边长为１ 的等边三角形拼成如图所示的图形， 用y 表示拼成的图形的周长， 用n表示其中等边三角形的数目， 显然拼成的图形的周长y是n的函数． 3 4 5 6 7 8 9 10 y=n+2(n为正整数)y=n+2(n为正整数)例1 某天7时， 小明从家骑自行车上学， 途中因自行车发生故障， 修车耽误了一段时间后继续骑行， 按时赶到了学校. 图反映了他骑车的整个过程， 结合图象， 回答下列问题：解（1）从横坐标看出， 自行车发生故障的时间是7:05； 从纵坐标看出， 此时离家1000 m.
举
例（1） 自行车发生故障是在什么时间？ 此时离家有多远？例1 某天7时， 小明从家骑自行车上学， 途中因自行车发生故障， 修车耽误了一段时间后继续骑行， 按时赶到了学校. 图反映了他骑车的整个过程， 结合图象， 回答下列问题：举
例（2） 修车花了多长时间？ 修好车后又花了多长时间到达学校？解（2）从横坐标看出， 小明修车花了15 min； 小明修好车后又花了10 min到达学校.例1 某天7时， 小明从家骑自行车上学， 途中因自行车发生故障， 修车耽误了一段时间后继续骑行， 按时赶到了学校. 图反映了他骑车的整个过程， 结合图象， 回答下列问题：举
例（3） 小明从家到学校的平均速度是多少？解（3）从纵坐标看出， 小明家离学校2100 m； 从横坐标看出， 他在路上共花了30 min， 因此， 他从家到学校的平均速度是2 100 ÷ 30 = 70 （m/min）.例2 王教授和孙子小强经常一起进行早锻炼，主要活动是爬山．有一天，小强让爷爷先上，然后追赶爷爷．图中两条线段分别表示小强和爷爷离开山脚的距离y （米）与爬山所用时间x （分）的关系（从小强开始爬山时计时）．⑴ 小强让爷爷先上多少米？
⑵ 山顶离山脚的距离有多少米？谁先爬上山顶？解：
⑴ 小强让爷爷先上60米；⑵ 山顶离山脚的距离有300米，小强先爬上山顶； 举
例(3)小强通过多少时间追上爷爷?解：
(3)小强经过8分钟追上爷爷.例2 王教授和孙子小强经常一起进行早锻炼，主要活动是爬山．有一天，小强让爷爷先上，然后追赶爷爷．图中两条线段分别表示小强和爷爷离开山脚的距离y （米）与爬山所用时间x （分）的关系（从小强开始爬山时计时）．举
例1. 如图， 将一个正方形的顶点分别标上号码1， 2， 3， 4，直线l经过第2， 4号顶点． 作这个正方形关于直线l 的轴对称图形， 那么正方形的各个顶点分别变成哪个顶点？ 填在下表中：这个表给出了y是x的函数． 画出它的图象， 它的图象由几个点组成？ 3 2 1 4 图象由4个点组成 3 2 1 4 2. 等腰三角形的底角的度数为x， 顶角的度数为y， 写出y 随x 而变化的函数表达式， 并指出自变量x 的取值范围.解3.如图是A 市某一天内的气温随时间而变化的函数图象， 结合图象回答下列问题：
（1） 这一天中的最高气温是多少？是上午时段， 还是下午时段？解（1） 最高气温是24°C, 是在14点，是下午时段;（2） 最高气温与最低气温相差多少？解（2） 最高气温是24°C, 最低气温是8°C，最高气温与最低气温相差24-8=16（°C）;3.如图是A 市某一天内的气温随时间而变化的函数图象， 结合图象回答下列问题：
（3） 什么时段， 气温在逐渐升高？什么时段， 气温在逐渐降低解（3） 在2点到14点，气温逐渐升高，在0点到2点，14点到24点气温逐渐降低.3.如图是A 市某一天内的气温随时间而变化的函数图象， 结合图象回答下列问题：
问题6：（1）函数的表示方法有哪些？（2）函数的三种表示方法各自的优点是什么？例1用固定的速度向如图所示形状的杯子里注水，则能表示杯子里水面的高度和注水时间的关系的大致图象是（ ）.C例2甲、乙两人在一次百米赛跑中，路程S（米）与赛跑时间t（秒）的关系如图所示，则下列说法正确的是（　　）
A．甲、乙两人的速度相同
B．甲先到达终点
C．乙用的时间短
D．乙比甲跑的路程多
B例3小芳的爷爷每天坚持体育锻炼，某天他慢步行走到离家较远的公园，打了一会儿太极拳，然后沿原路跑步到家里，下面能够反映当天小芳爷爷离家的距离y（米）与时间x（分钟）之间的关系的大致图象是（　　）
C有下列说法：
①“龟兔再次赛跑”的路为1000米；
②兔子和乌龟同时从起点出发；
③乌龟在途中休息了10分钟；
④兔子在途中750米处追上乌龟．
其中正确的说法是　 　．
(把你认为正确说法的序号都填上)例4“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了
“龟兔再次赛跑”的故事（x表示乌龟从起点出发所行的
时间，y1表示乌龟所行的路程，y2表示兔子所行的路程）．①③④（1）当用电量是180千瓦时时，电费
是 元；
（2）第二档的用电量范围是 ；
（3）“基本电价”是 元/千瓦时；
（4）小明家8月份的电费是328.5元，这个月他家用电多少千瓦时？例5为了响应国家节能减排的号召，鼓励市民节约用电，我市从2012年7月1日起，居民用电实行“一户一表”的“阶梯电价”，分三个档次收费，第一档是用电量不超过180千瓦时实行“基本电价”，第二、三档实行“提高电价”，具体收费情况如右折线图，请根据图像回答下列问题；108180单位：北京市第一六六中学
姓名：孙梅