2015春湘教版数学八下4.5《一次函数的应用》课件3(共45张PPT)
文档属性
| 名称 | 2015春湘教版数学八下4.5《一次函数的应用》课件3(共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-02 08:27:22 | ||
图片预览











文档简介
课件45张PPT。一次函数的应用4.5 某地为保护环境,鼓励节约用电,实行阶梯电价
制度. 规定每户居民每月用电量不超过160kW·h,则按
0.6元/(kW·h)收费;若超过160kW·h,则超出部分
每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与所用的
电量x(kW·h)之间的函数表达式;
(2)画出这个函数的图象;
(3)小王家3月份,4 月份分别用电150kW·h和200kW·h,
应缴纳电费各多少元?(2) 该函数的图象如图4-16. 该函数图象由两个
一次函数的图象拼接在
一起.图4-16由于小红比小明晚出发2 h,因此小红所用时间 为(x - 2)h. 从而 y2 = 40(x - 2),自变量x 的取值范围是2≤x≤3. (1)分别写出y1 ,y2与x之间的函数表达式; 过点M(0,40)作射线l 与x 轴平行,它先与射线
y2 = 40(x - 2)相交,这表明小红先到达乙地.
(2)在同一个直角坐标系中,画出这两个函数的图象,
并指出谁先到达乙地.
1. 某音像店对外出租光盘的收费标准是:每张光盘在出租后头两天的租金为0.8 元/ 天,以后每天收0.5 元. 求一张光盘在租出后第n天的租金y(元)与时间t(天)之间的函数表达式. 2. 某移动公司对于移动话费推出两种收费方式:
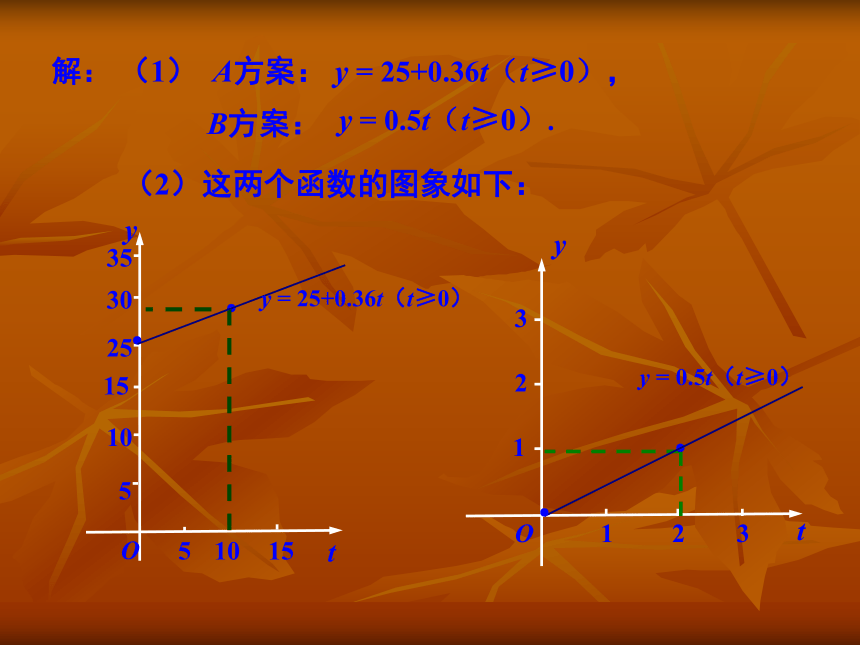
A方案:每月收取基本月租费25元,另收通话费
为0.36元/min;
B方案: 零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
(3)若林先生每月通话300 min,他选择哪种付费
方式比较合算?(2)这两个函数的图象如下:(3)当t=300时,A方案:
y = 25+0.36t=25+0.36×300=133(元);
B方案:
y = 0.5t=0.5×300=150(元).
所以此时采用A方案比较合算. 国际奥林匹克运动会早期,男子撑杆跳高的纪录近似值如下表所示: 观察这个表中第二行的数据,可以为奥运会的撑杆跳高纪录与时间的关系建立函数模型吗? 上表中每一届比上一届的纪录提高了0.2m,可以
试着建立一次函数的模型.解得 b = 3.3, k=0.05.公式①就是奥运会早期男子撑杆跳高纪录y与时间t
的函数关系式.当t = 8时, y = 3.73,这说明1908年的撑杆跳高
纪录也符合公式①. 能够利用上面得出的
公式①预测1912年奥运会
的男子撑杆跳高纪录吗? 实际上,1912 年奥运会男子撑杆跳高纪录约为3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.y=0.05×12+3.33=3.93. 能够利用公式①预测
20世纪80年代,譬如
1988年奥运会男子撑杆
跳高纪录吗?
然而,1988年奥运会的男子撑杆跳高纪录是5.90 m,
远低于7.73 m. 这表明用所建立的函数模型远离已知数据
做预测是不可靠的.y=0.05×88+3.33=7.73.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:例2(1) 求身高y与指距x之间的函数表达式;
(2) 当李华的指距为22cm时,你能预测他的身高吗?(1) 求身高y与指距x之间的函数表达式;解得k = 9, b = -20.
于是y = 9x -20. ①将x = 21,y = 169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.解 当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.(2) 当李华的指距为22cm时,你能预测他的身高吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3)能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的
次数吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3) 能用所求出的函数模型来预测蟋蟀在0 ℃时所
鸣叫次数吗?答:不能,因为此函数关系是近似的,与实际
生活中的情况有所不符,蟋蟀在0 ℃时可能
不会鸣叫.2. 某商店今年7月初销售纯净水的数量如下表所示:(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量. 解 销售纯净水的数量y(瓶)与时间t的
函数关系式是
y= 160+(t-1)×5= 5t+155.(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量.一次函数y = 5 - x的图象如图4-18所示.
(1) 方程x + y = 5 的解有多少个? 写出其中的几个.
(2) 在直角坐标系中分别描出以这些解为坐标的点,
它们在一次函数y = 5 - x的图象上吗?图4-18(3) 在一次函数y = 5 - x的图象上任取一点,它的
坐标满足方程x + y = 5吗?
(4) 以方程x + y = 5 的解为坐标的所有点组成的
图象与一次函数y = 5 - x的图象相同吗?图4-18 事实上, 以二元一次方程x + y = 5的解为坐标
的点所组成的图形与一次函数y = 5 - x的图象完全相同. 我们知道二元一次方程x + y = 5的解有无数组,
以这些解为坐标的点在一次函数y = 5 - x的图象上.
将方程x + y = 5化成一次函数的形式:y = 5 - x ,
易知该一次函数的图象上任意一点的坐标也满足
方程x + y = 5. 一般地, 一次函数y = kx + b 图象上任意一点
的坐标都是二元一次方程kx-y + b = 0 的一个解,
以二元一次方程kx- y + b = 0的解为坐标的点都在
一次函数y = kx + b的图象上.你能找到下面两个问题之间的联系吗?
(1) 解方程: 3x - 6 = 0.
(2) 已知一次函数y = 3x - 6,问x取何值时,y = 0?
从图中可以看出,一次函数y = 3x - 6的图象与
x 轴交于点(2,0), 这就是当y = 0 时,得x = 2, 而x = 2正是方程3x - 6 = 0的解.(1) 方程3x - 6 = 0的解为x = 2.(2) 画出函数y = 3x - 6的图象(如图4-19),图4-19 一般地,一次函数y = kx + b (k≠0) 的图象
与x 轴的交点的横坐标是一元一次方程kx + b = 0的解.
任何一个一元一次方程kx + b = 0 的解, 就是一次
函数y = kx + b 的图象与x 轴交点的横坐标.已知一次函数y = 2x + 6, 求这个函数的图象
与x轴交点的横坐标.直线y = 2x + 6与x 轴交于点(-3,0),所以该图象与x轴交点的横坐标为-3. 上面这两种解法分别从“数” 与“形” 的角
度出发来解决问题. 1. 把下列二元一次方程改写成y = kx + b的形式.
(1) 3x + y = 7; (2) 3x + 4y = 13. 解 (1) y = -3x+ 7;
(2) y =2. 已知函数y = 3x + 9,自变量满足什么条件时,y = 0?答:x= -3.3. 利用函数图象, 解方程3x - 9 = 0.所以方程3x - 9 = 0 的解为x= 3.直线 y = 3x + 9与 x轴交于点(3,0),
1. 举例说明什么是函数,指出其中的自变量和因变量.
2. 函数有哪些表示方法? 它们各有什么特点?
3. 什么是一次函数?什么是正比例函数?它们之间有
什么关系?4. 正比例函数y = kx 的图象与一次函数y = kx + b(k≠0) 的图象有何关系?它们各具有什么性质?
5. 举例说明如何用待定系数法求一次函数的表达式.
6. 一次函数与二元一次方程有何关系?
制度. 规定每户居民每月用电量不超过160kW·h,则按
0.6元/(kW·h)收费;若超过160kW·h,则超出部分
每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与所用的
电量x(kW·h)之间的函数表达式;
(2)画出这个函数的图象;
(3)小王家3月份,4 月份分别用电150kW·h和200kW·h,
应缴纳电费各多少元?(2) 该函数的图象如图4-16. 该函数图象由两个
一次函数的图象拼接在
一起.图4-16由于小红比小明晚出发2 h,因此小红所用时间 为(x - 2)h. 从而 y2 = 40(x - 2),自变量x 的取值范围是2≤x≤3. (1)分别写出y1 ,y2与x之间的函数表达式; 过点M(0,40)作射线l 与x 轴平行,它先与射线
y2 = 40(x - 2)相交,这表明小红先到达乙地.
(2)在同一个直角坐标系中,画出这两个函数的图象,
并指出谁先到达乙地.
1. 某音像店对外出租光盘的收费标准是:每张光盘在出租后头两天的租金为0.8 元/ 天,以后每天收0.5 元. 求一张光盘在租出后第n天的租金y(元)与时间t(天)之间的函数表达式. 2. 某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费25元,另收通话费
为0.36元/min;
B方案: 零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
(3)若林先生每月通话300 min,他选择哪种付费
方式比较合算?(2)这两个函数的图象如下:(3)当t=300时,A方案:
y = 25+0.36t=25+0.36×300=133(元);
B方案:
y = 0.5t=0.5×300=150(元).
所以此时采用A方案比较合算. 国际奥林匹克运动会早期,男子撑杆跳高的纪录近似值如下表所示: 观察这个表中第二行的数据,可以为奥运会的撑杆跳高纪录与时间的关系建立函数模型吗? 上表中每一届比上一届的纪录提高了0.2m,可以
试着建立一次函数的模型.解得 b = 3.3, k=0.05.公式①就是奥运会早期男子撑杆跳高纪录y与时间t
的函数关系式.当t = 8时, y = 3.73,这说明1908年的撑杆跳高
纪录也符合公式①. 能够利用上面得出的
公式①预测1912年奥运会
的男子撑杆跳高纪录吗? 实际上,1912 年奥运会男子撑杆跳高纪录约为3.93 m. 这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.y=0.05×12+3.33=3.93. 能够利用公式①预测
20世纪80年代,譬如
1988年奥运会男子撑杆
跳高纪录吗?
然而,1988年奥运会的男子撑杆跳高纪录是5.90 m,
远低于7.73 m. 这表明用所建立的函数模型远离已知数据
做预测是不可靠的.y=0.05×88+3.33=7.73.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:例2(1) 求身高y与指距x之间的函数表达式;
(2) 当李华的指距为22cm时,你能预测他的身高吗?(1) 求身高y与指距x之间的函数表达式;解得k = 9, b = -20.
于是y = 9x -20. ①将x = 21,y = 169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.解 当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.(2) 当李华的指距为22cm时,你能预测他的身高吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3)能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的
次数吗? (1)根据表中数据确定该一次函数的表达式;(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约
为多少摄氏度? (3) 能用所求出的函数模型来预测蟋蟀在0 ℃时所
鸣叫次数吗?答:不能,因为此函数关系是近似的,与实际
生活中的情况有所不符,蟋蟀在0 ℃时可能
不会鸣叫.2. 某商店今年7月初销售纯净水的数量如下表所示:(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量. 解 销售纯净水的数量y(瓶)与时间t的
函数关系式是
y= 160+(t-1)×5= 5t+155.(1)你能为销售纯净水的数量与时间之间的关系
建立函数模型吗?(2)用所求出的函数解析式预测今年7月5日该商店
销售纯净水的数量.一次函数y = 5 - x的图象如图4-18所示.
(1) 方程x + y = 5 的解有多少个? 写出其中的几个.
(2) 在直角坐标系中分别描出以这些解为坐标的点,
它们在一次函数y = 5 - x的图象上吗?图4-18(3) 在一次函数y = 5 - x的图象上任取一点,它的
坐标满足方程x + y = 5吗?
(4) 以方程x + y = 5 的解为坐标的所有点组成的
图象与一次函数y = 5 - x的图象相同吗?图4-18 事实上, 以二元一次方程x + y = 5的解为坐标
的点所组成的图形与一次函数y = 5 - x的图象完全相同. 我们知道二元一次方程x + y = 5的解有无数组,
以这些解为坐标的点在一次函数y = 5 - x的图象上.
将方程x + y = 5化成一次函数的形式:y = 5 - x ,
易知该一次函数的图象上任意一点的坐标也满足
方程x + y = 5. 一般地, 一次函数y = kx + b 图象上任意一点
的坐标都是二元一次方程kx-y + b = 0 的一个解,
以二元一次方程kx- y + b = 0的解为坐标的点都在
一次函数y = kx + b的图象上.你能找到下面两个问题之间的联系吗?
(1) 解方程: 3x - 6 = 0.
(2) 已知一次函数y = 3x - 6,问x取何值时,y = 0?
从图中可以看出,一次函数y = 3x - 6的图象与
x 轴交于点(2,0), 这就是当y = 0 时,得x = 2, 而x = 2正是方程3x - 6 = 0的解.(1) 方程3x - 6 = 0的解为x = 2.(2) 画出函数y = 3x - 6的图象(如图4-19),图4-19 一般地,一次函数y = kx + b (k≠0) 的图象
与x 轴的交点的横坐标是一元一次方程kx + b = 0的解.
任何一个一元一次方程kx + b = 0 的解, 就是一次
函数y = kx + b 的图象与x 轴交点的横坐标.已知一次函数y = 2x + 6, 求这个函数的图象
与x轴交点的横坐标.直线y = 2x + 6与x 轴交于点(-3,0),所以该图象与x轴交点的横坐标为-3. 上面这两种解法分别从“数” 与“形” 的角
度出发来解决问题. 1. 把下列二元一次方程改写成y = kx + b的形式.
(1) 3x + y = 7; (2) 3x + 4y = 13. 解 (1) y = -3x+ 7;
(2) y =2. 已知函数y = 3x + 9,自变量满足什么条件时,y = 0?答:x= -3.3. 利用函数图象, 解方程3x - 9 = 0.所以方程3x - 9 = 0 的解为x= 3.直线 y = 3x + 9与 x轴交于点(3,0),
1. 举例说明什么是函数,指出其中的自变量和因变量.
2. 函数有哪些表示方法? 它们各有什么特点?
3. 什么是一次函数?什么是正比例函数?它们之间有
什么关系?4. 正比例函数y = kx 的图象与一次函数y = kx + b(k≠0) 的图象有何关系?它们各具有什么性质?
5. 举例说明如何用待定系数法求一次函数的表达式.
6. 一次函数与二元一次方程有何关系?
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
