2015春湘教版数学八下4.3《一次函数的图象》课件2(共22张PPT)
文档属性
| 名称 | 2015春湘教版数学八下4.3《一次函数的图象》课件2(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 988.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-02 08:30:14 | ||
图片预览





文档简介
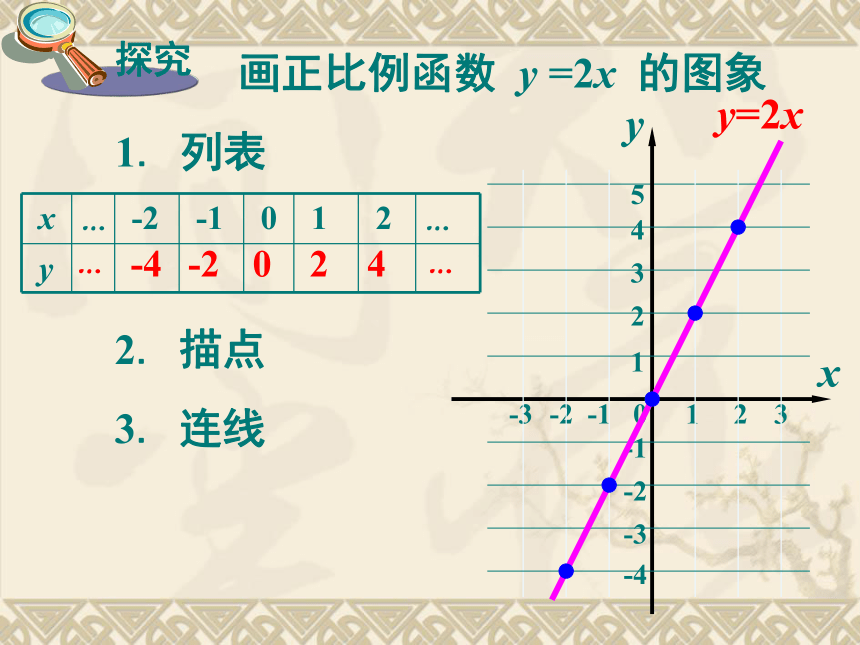
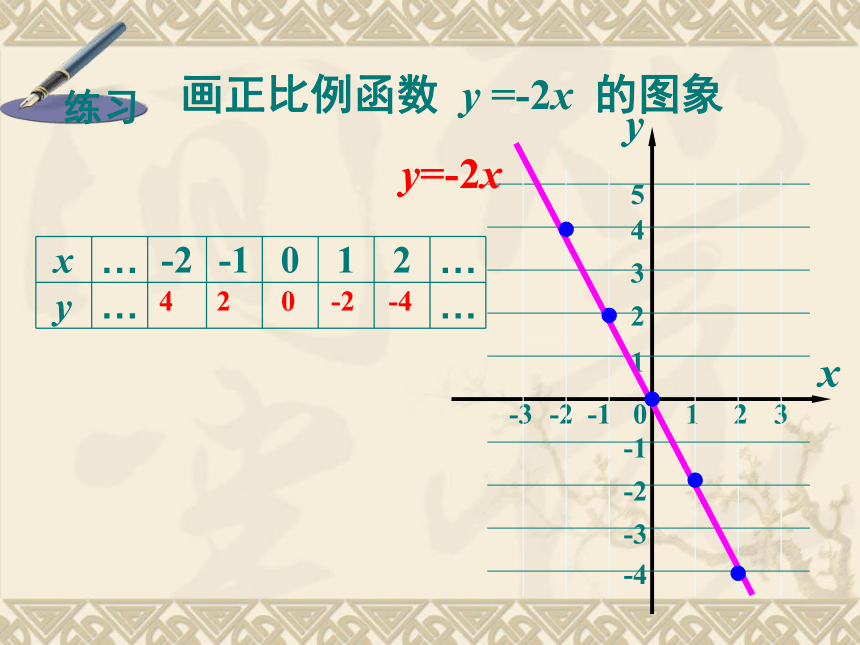
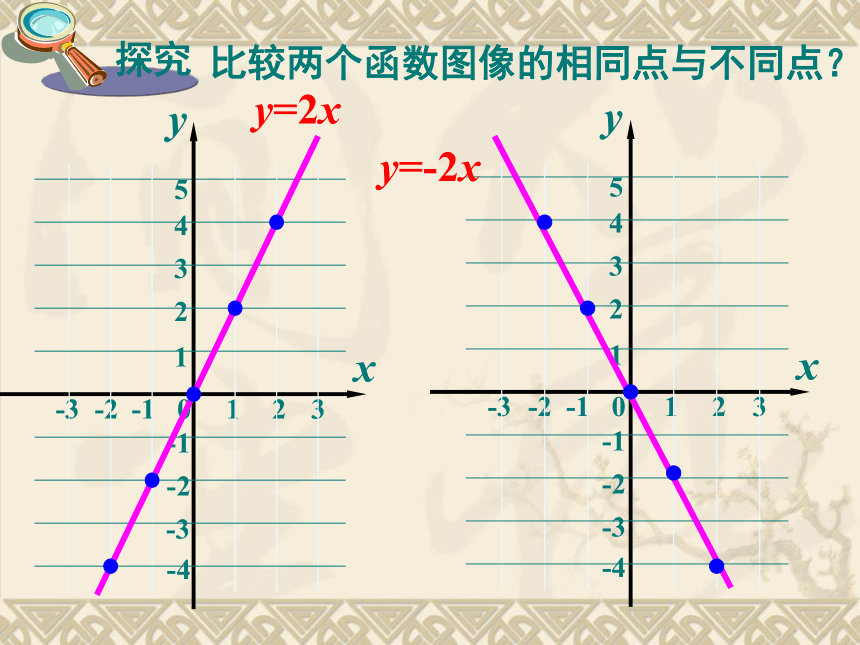
课件22张PPT。 一次函数的图象4.3-4-2024y=2x画正比例函数 y =2x 的图象1. 列表2. 描点3. 连线……y=-2x画正比例函数 y =-2x 的图象420-2-4比较两个函数图像的相同点与不同点?
1.两图象都是经过原点的 ,
2.函数y=2x的图象从左向右 ,经过
第 象限,y随x的增大而 ;
函数y=-2x的图象从左向右 ,经过
第 象限,y随x的增大而 。 直线上升一、三下降二、四增大减小 通过以上学习,画正比例函数y=kx图象有无简便的办法?
画正比例函数图象时,只需在原点外再确定一个点,
即找出一组满足函数关系式的对应数值即可,如(0,0)(1 ,k).因为两点可以确定一条直线.
函数y=kx的图象是经过原点(0,0)与点(1 ,k)的直线.
1.函数y =-4x的图象在第 象限,经过
点(0, )与点(1, ),y 随x的增大而 ;2.如果函数y =(m-2)x 的图象经过第一、三象限,那么m 的取值范围是 ;二、四0-4减小m>23.函数y=0.3x的图象经过点(0, )和(1, ), y随x的增大而 .00.3增大举
例举
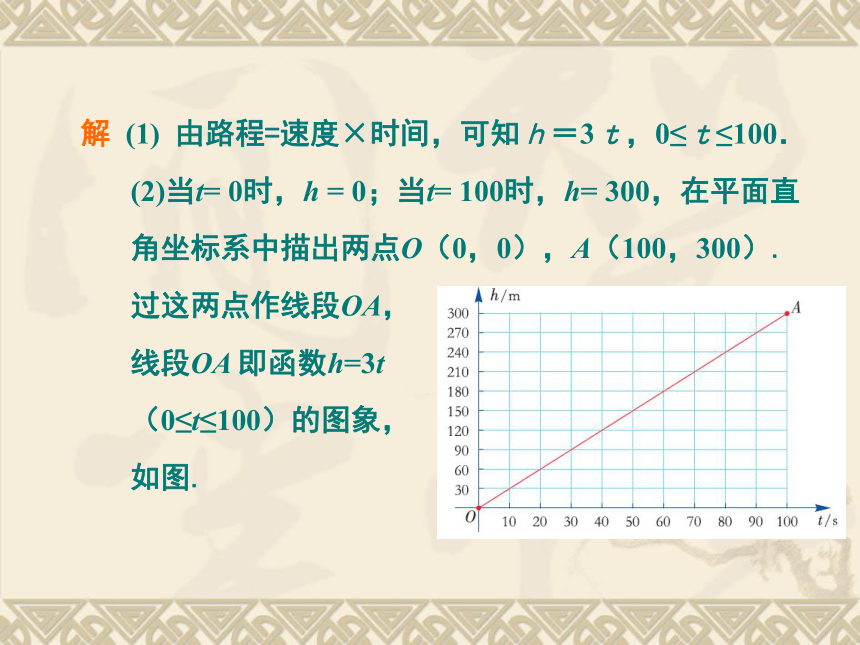
例例 某国家森林公园的一个旅游景点的电梯运行时,以
3m/s 的速度上升,运行总高度为300 m.
(1) 求电梯运行高度h(m)随运行时间t(s)而变化的函
数表达式;
(2) 画出这个函数的图象.解 (1) 由路程=速度×时间,可知h=3t,0≤t≤100.(2)当t= 0时,h = 0;当t= 100时,h= 300,在平面直角坐标系中描出两点O(0,0),A(100,300). 过这两点作线段OA,
线段OA 即函数h=3t
(0≤t≤100)的图象,
如图.用描点法在同一坐标系中画出函数y =-6x,y=-6x+5的图象.
xyo15观察两个函数图象,发现:
相同点: .
不同点: .
联系: .y =-6x+5y =-6x解:都是直线;倾斜程度相同;…y=-6x的图象过原点;y =-6x+5的图象与y轴交于(0,5)点;…y=-6x+5的图象可以看作是y =-6x的图象向上平移5个长度单位得到;…1260-6-1217115-1-7用描点法在同一坐标系中画出函数y =-6x,y=-6x+5的图象.
xyo15y =-6x+5y =-6x解:1260-6-1217115-1-7比较两个函数的解析式(表格),你能解释两个函数图象的位置关系吗?用描点法在同一坐标系中画出函数y =-6x,y=-6x+5的图象.
xyo15y =-6x+5y =-6x解:1260-6-1217115-1-7(1)一次函数y = kx+b的图象是 ,称它
为直线y=kx+b.图象与y轴的交点为 。
(2)直线y=kx+b(k≠0)可以看作是直线y=kx平
移 单位长度而得到。当b>0时,
向 平移,当b<0时,向 平移。直线| b |上(0,b)下联系上面问题,考虑一次函数y = kx+b的图象是什么形状,它与直线y = kx有什么关系?画出函数y=2x-1的图象.∴ 过(0,-1) ( ,0)作直线y=2x-1 . ···· y=2x-1y=-2x+l解:练习:画出函数y = -2x+1的图象. 观察画出的一次函数y=2x+1,y=-2x+1的图象,你能发现当自变量x的取值由小变大时,对应的函数值如何变化吗? 直线y=2x+1的图象,由左到右逐渐 (上升、下降)因此,y随x的增大而 (增大、减小)
直线y=-2x+1的图象,由左到右逐渐 (上升、下降)因此,y随x的增大而 (增大、减小)上升增大下降减小
一次函数y=kx+b中,k的正负对函数图象有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大。
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小。举
例例:图4-13描述了某一天小亮从家
骑车去书店购书,然后又骑车回家
的情况.你能说出小亮在路上的情
形吗?分析:小亮骑车离家的距离y 是时间x的函数,这个函数图象由3条线段组成,每一条线段代表一个阶段的活动.举
例解:第一段是从原点出发的线段OA.
从横坐标看出,小亮路上花了30min,
当横坐标从0变化到30时,纵坐标均
匀增加,这说明小亮从家出发匀速前
进30min,到达书店.举
例解:第二段是与x轴平行的一条线段
AB,当横坐标从30变化到60时,纵坐
标没有变化,这说明小亮在书店购书
待了30min.举
例解:第三段是与x轴有交点的线段BC.
从横坐标看出,小亮路上花了40min.
当横坐标从60变化到100时,纵坐标均
匀减少,这说明小亮从书店出发匀速
前进40min,返回家中.比较第一段与第三段线段,发现第一段更“陡”,这说明去书店的速度更快,而回家的速度要慢一些.(1).下列函数中,y的值随x值的增大而增大的函数是________. A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2C(2).直线y=3x-2可由直线y=3x向 平移 单位得到.(3).直线y=x+2可由直线y=x-1向 平
移 单位得到。下2上32.一次函数的图象与性质是什么,常数k,b的意义和作用又是什么?.1.如何画正比例函数、一次函数的图象?例1 对于函数y=5x+6,y的值随x的值减小 而______. 例2 函数y=2x-1经过 象限.减少一、三、四
1.两图象都是经过原点的 ,
2.函数y=2x的图象从左向右 ,经过
第 象限,y随x的增大而 ;
函数y=-2x的图象从左向右 ,经过
第 象限,y随x的增大而 。 直线上升一、三下降二、四增大减小 通过以上学习,画正比例函数y=kx图象有无简便的办法?
画正比例函数图象时,只需在原点外再确定一个点,
即找出一组满足函数关系式的对应数值即可,如(0,0)(1 ,k).因为两点可以确定一条直线.
函数y=kx的图象是经过原点(0,0)与点(1 ,k)的直线.
1.函数y =-4x的图象在第 象限,经过
点(0, )与点(1, ),y 随x的增大而 ;2.如果函数y =(m-2)x 的图象经过第一、三象限,那么m 的取值范围是 ;二、四0-4减小m>23.函数y=0.3x的图象经过点(0, )和(1, ), y随x的增大而 .00.3增大举
例举
例例 某国家森林公园的一个旅游景点的电梯运行时,以
3m/s 的速度上升,运行总高度为300 m.
(1) 求电梯运行高度h(m)随运行时间t(s)而变化的函
数表达式;
(2) 画出这个函数的图象.解 (1) 由路程=速度×时间,可知h=3t,0≤t≤100.(2)当t= 0时,h = 0;当t= 100时,h= 300,在平面直角坐标系中描出两点O(0,0),A(100,300). 过这两点作线段OA,
线段OA 即函数h=3t
(0≤t≤100)的图象,
如图.用描点法在同一坐标系中画出函数y =-6x,y=-6x+5的图象.
xyo15观察两个函数图象,发现:
相同点: .
不同点: .
联系: .y =-6x+5y =-6x解:都是直线;倾斜程度相同;…y=-6x的图象过原点;y =-6x+5的图象与y轴交于(0,5)点;…y=-6x+5的图象可以看作是y =-6x的图象向上平移5个长度单位得到;…1260-6-1217115-1-7用描点法在同一坐标系中画出函数y =-6x,y=-6x+5的图象.
xyo15y =-6x+5y =-6x解:1260-6-1217115-1-7比较两个函数的解析式(表格),你能解释两个函数图象的位置关系吗?用描点法在同一坐标系中画出函数y =-6x,y=-6x+5的图象.
xyo15y =-6x+5y =-6x解:1260-6-1217115-1-7(1)一次函数y = kx+b的图象是 ,称它
为直线y=kx+b.图象与y轴的交点为 。
(2)直线y=kx+b(k≠0)可以看作是直线y=kx平
移 单位长度而得到。当b>0时,
向 平移,当b<0时,向 平移。直线| b |上(0,b)下联系上面问题,考虑一次函数y = kx+b的图象是什么形状,它与直线y = kx有什么关系?画出函数y=2x-1的图象.∴ 过(0,-1) ( ,0)作直线y=2x-1 . ···· y=2x-1y=-2x+l解:练习:画出函数y = -2x+1的图象. 观察画出的一次函数y=2x+1,y=-2x+1的图象,你能发现当自变量x的取值由小变大时,对应的函数值如何变化吗? 直线y=2x+1的图象,由左到右逐渐 (上升、下降)因此,y随x的增大而 (增大、减小)
直线y=-2x+1的图象,由左到右逐渐 (上升、下降)因此,y随x的增大而 (增大、减小)上升增大下降减小
一次函数y=kx+b中,k的正负对函数图象有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大。
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小。举
例例:图4-13描述了某一天小亮从家
骑车去书店购书,然后又骑车回家
的情况.你能说出小亮在路上的情
形吗?分析:小亮骑车离家的距离y 是时间x的函数,这个函数图象由3条线段组成,每一条线段代表一个阶段的活动.举
例解:第一段是从原点出发的线段OA.
从横坐标看出,小亮路上花了30min,
当横坐标从0变化到30时,纵坐标均
匀增加,这说明小亮从家出发匀速前
进30min,到达书店.举
例解:第二段是与x轴平行的一条线段
AB,当横坐标从30变化到60时,纵坐
标没有变化,这说明小亮在书店购书
待了30min.举
例解:第三段是与x轴有交点的线段BC.
从横坐标看出,小亮路上花了40min.
当横坐标从60变化到100时,纵坐标均
匀减少,这说明小亮从书店出发匀速
前进40min,返回家中.比较第一段与第三段线段,发现第一段更“陡”,这说明去书店的速度更快,而回家的速度要慢一些.(1).下列函数中,y的值随x值的增大而增大的函数是________. A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2C(2).直线y=3x-2可由直线y=3x向 平移 单位得到.(3).直线y=x+2可由直线y=x-1向 平
移 单位得到。下2上32.一次函数的图象与性质是什么,常数k,b的意义和作用又是什么?.1.如何画正比例函数、一次函数的图象?例1 对于函数y=5x+6,y的值随x的值减小 而______. 例2 函数y=2x-1经过 象限.减少一、三、四
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
