冀教版七年级数学下册6.3《二元一次方程组的应用》课件(共44张PPT)
文档属性
| 名称 | 冀教版七年级数学下册6.3《二元一次方程组的应用》课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 592.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-02 08:33:41 | ||
图片预览





文档简介
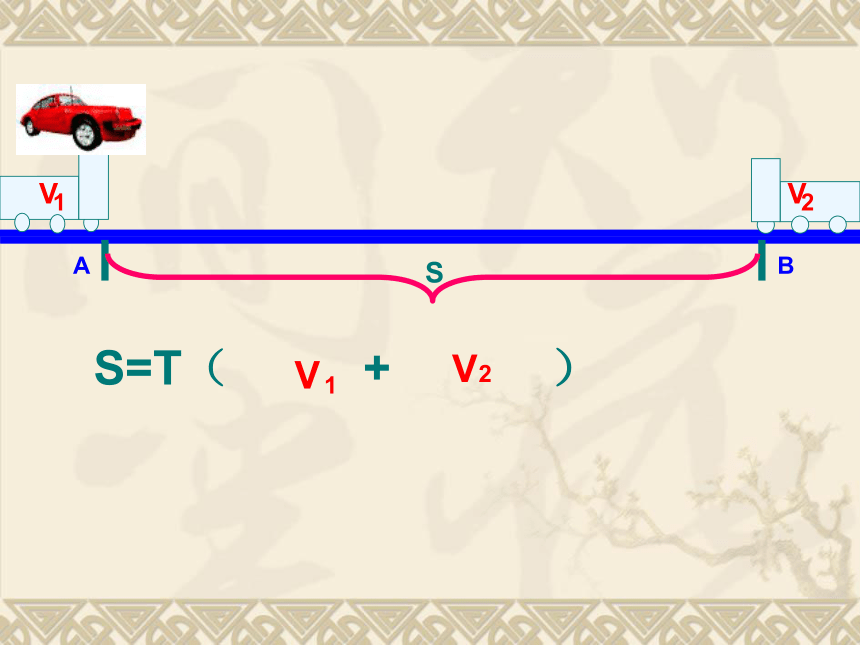
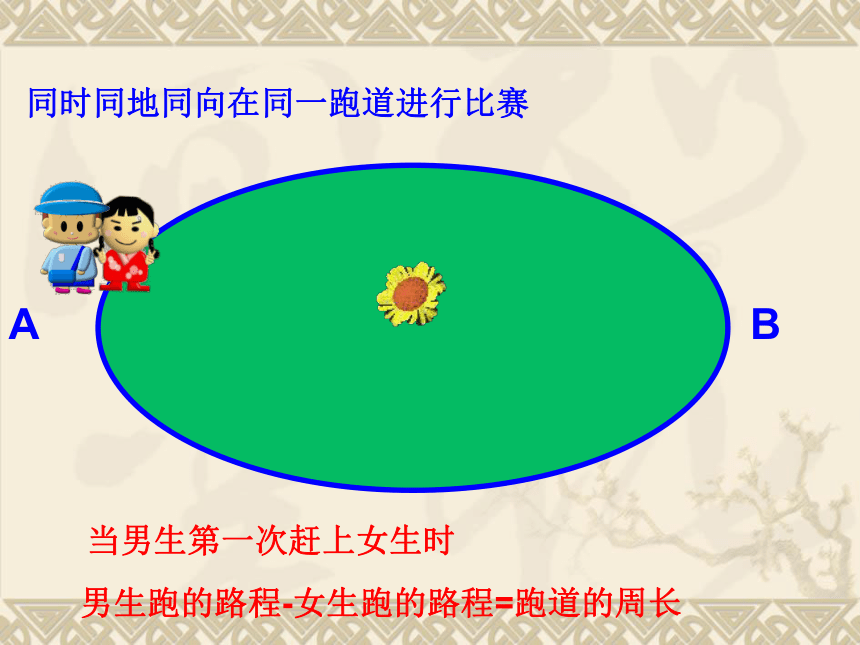
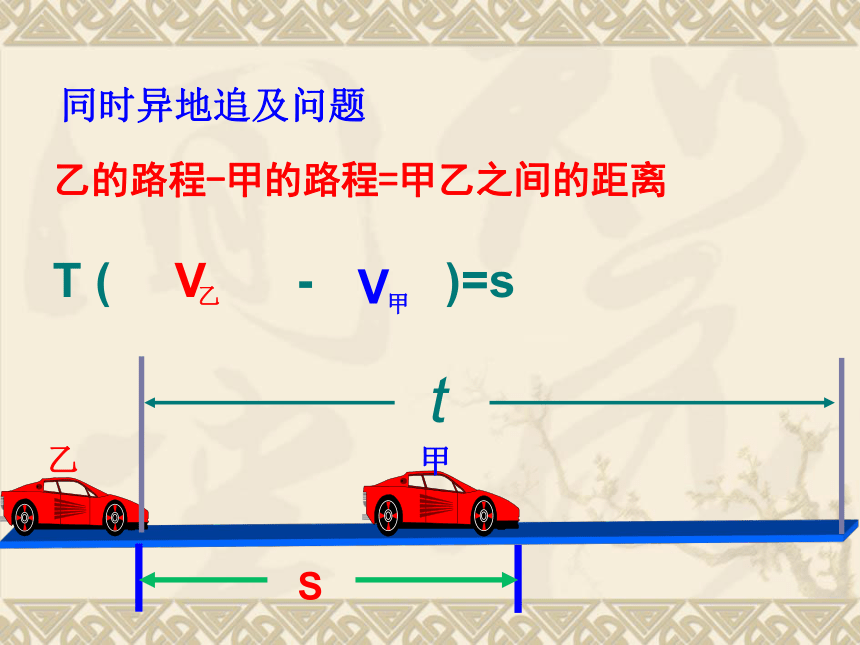
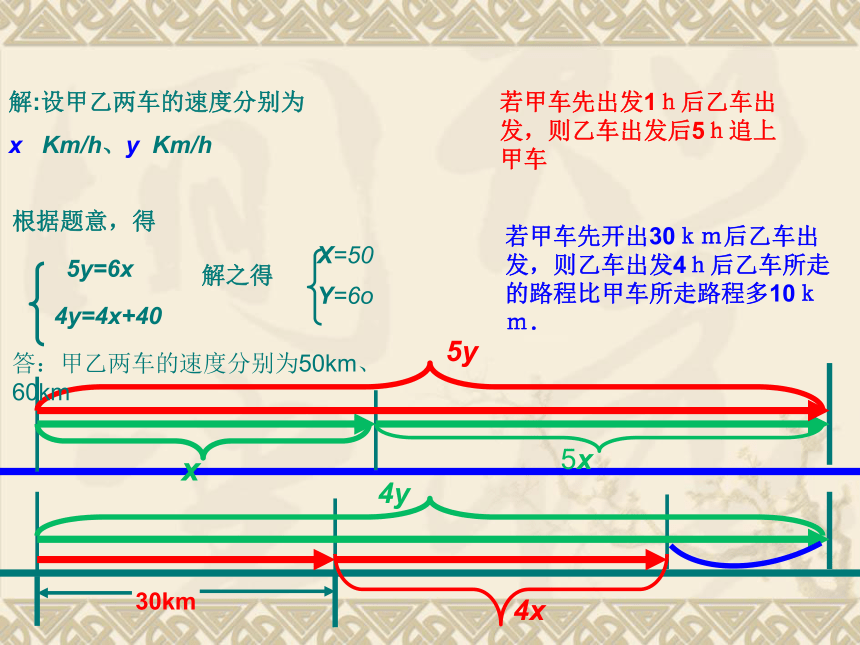
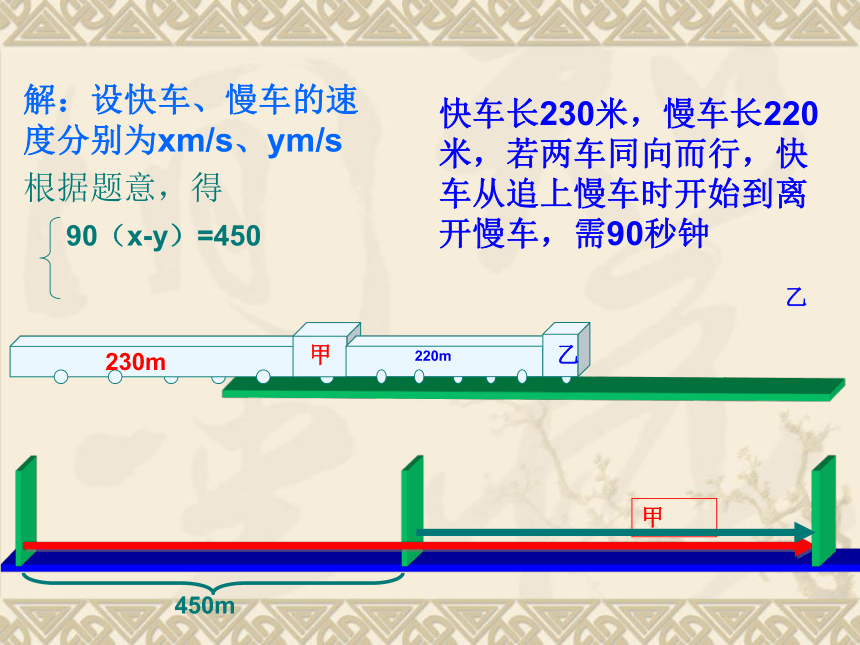
课件44张PPT。实践与探索(二元一次方程组的应用)一、行程问题基本数量关系路程=时间×速度时间=路程/速度速度=路程/时间同时相向而行路程=时间×速度之和同时同向而行路程=时间×速度之差船在顺水中的速度=船在静水中的速度+水流的速度船在逆水中的速度=船在静水中的速度-水流的速度AB同时同地同向在同一跑道进行比赛当男生第一次赶上女生时男生跑的路程-女生跑的路程=跑道的周长乙甲同时异地追及问题乙的路程-甲的路程=甲乙之间的距离例1.某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车解:设甲乙两车的速度分别为
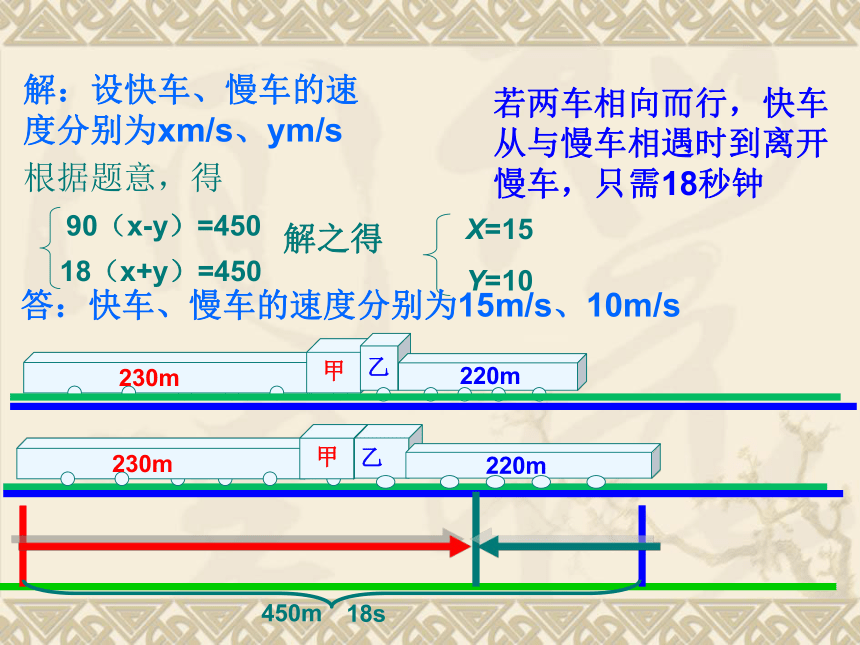
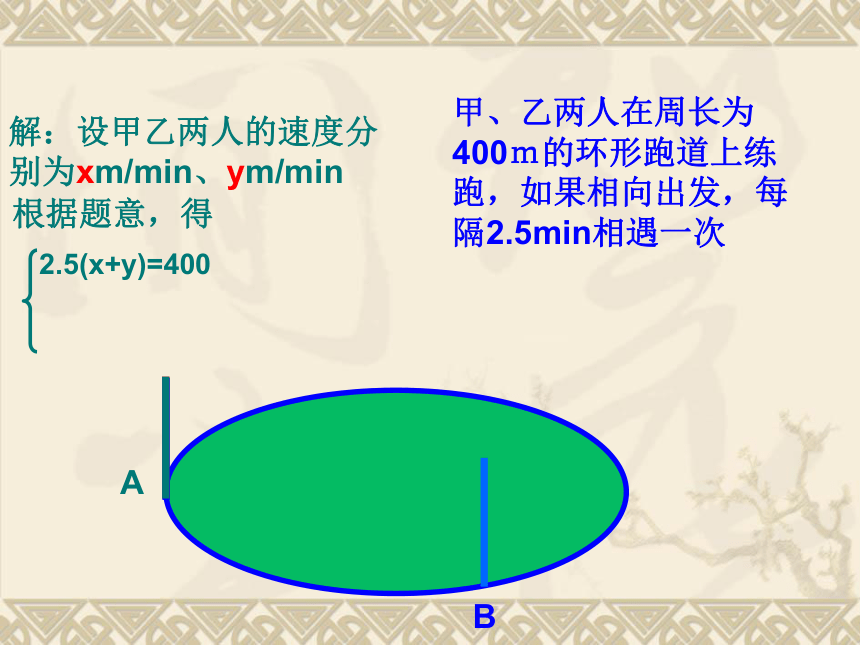
x Km/h、y Km/h根据题意,得5y=6x若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.4y=4x+40解之得答:甲乙两车的速度分别为50km、60km例2.一列快车长230米,一列慢车长220米,若两车同向而行,快车从追上慢车时开始到离开慢车,需90秒钟;若两车相向而行,快车从与慢车相遇时到离开慢车,只需18秒钟,问快车和慢车的速度各是多少?快车长230米,慢车长220米,若两车同向而行,快车从追上慢车时开始到离开慢车,需90秒钟乙若两车相向而行,快车从与慢车相遇时到离开慢车,只需18秒钟18(x+y)=450解之得答:快车、慢车的速度分别为15m/s、10m/s例3.甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次;如果同向出发,每隔10min相遇一次,假定两人速度不变,且甲快乙慢,求甲、乙两人的速度.甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次甲、乙两人在周长为400m的环形跑道上练跑,如果同向出发,每隔10min相遇一次10(X-Y)=400解之得答:甲乙两人的速度分别为100m/min、60m/min环形跑道追及问题等同于异地追及问题例4.已知A、B两码头之间的距离为240km,一艏船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.练习.一辆汽车从甲地驶往乙地,途中要过一桥。用相同时间,若车速每小时60千米,就能越过桥2千米;若车速每小时50千米,就差3千米才到桥。问甲地与桥相距多远?用了多长时间?轮船航向船在逆水中的速度=船在
静水中的速度-水流的速度船在顺水中的速度=船在
静水中的速度+水流的速度例5.已知A、B两码头之间的距离为240km,一艏船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.解:设船在静水中的速度及水流的速度分别为xkm/h、ykm/h,根据题意,得答:船在静水中的速度及水流的速度分别为50km/h、10km/h二、工程问题 工作量=工作时间×工作效率 工作效率=工作量/工作时间、工作时间=工作量/工作效率 例1.某工人原计划在限定时间内加工一批零件.如果每小时加工10个零件,就可以超额完成3 个;如果每小时加工11个零件就可以提前1h完成.问这批零件有多少个?按原计划需多少小时 完成?解:设这批零件有x个,按原计划需y小时完成,根据题意,得答:这批零件有77个,按计划需8 小时完成例2.甲乙两家服装厂生产同一规格的上衣和裤子,甲厂每月(按30天计算)用16天生产上衣,14天做裤子,共生产448套衣服(每套上、下衣各一件);乙厂每月用12天生产上衣,18天生产裤子,共生产720套衣服,两厂合并后,每月按现有能力最多能生产多少套衣服?填写下表16144481218720解:设该厂用x天生产上衣,y天生产裤子,则共生产( )x套衣服,由题意得448/16+720/12X+y=30(448/16+720/12)x=(448/14+720/18)y所以88x=88·13.5=1188三、商品经济问题本息和=本金+利息利息=本金×年利率×期数×利息税利息所得税=利息金额×20℅例1李明以两种形式分别储蓄了2000元和1000元,一年后全部取出,扣除利息所得税后可得利息43.92元,已知这两种储蓄的年利率的和为3.24℅,问这两种储蓄的年利率各是几分之几?(注:公民应交利息所得税=利息金额×20℅)解:设这两种储蓄的年利率分别是x、y,根据题意得答:这两种储蓄的年利蓄分别为2.25%、0.09%例2。某超市在“五一”期间寻顾客实行优惠,规定如下:(2)若顾客在该超市一次性购物 x元,当小于500元但不小于200元时,他实际付款 元;当x大于或等于500元时,他实际付款 元(用的代数式表示)(1)王老师一次购物600元,他实际付款 元 5300.9x0.8x+50解:设第一次购物的货款为x元,第二次购物的货款为y元①当x<200,则,y≥500,由题意得②当x小于500元但不小于200元时,y ≥ 500,由题意得③当均小于500元但不小于200元时,且,由题意 得综上所述,两次购物的分别为110元、710元或220元、600元此方程组无解.四、配套问题(一)配套与人员分配问题例1.某车间22名工人生产螺钉与螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母,为了使每天生产的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?一个螺钉配两个螺母螺钉数:螺母数=1:2解:设分配名x工人生产螺钉,y名工人生产螺母,则一天生产的螺钉数为1200x个,生产的螺母数为2000y个.所以为了使每天生产的产品刚好配套,应安排10人生产螺钉,12人生产螺母例2.某工地需雪派48人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应该怎样安排人员,正好能使挖的土能及时运走?每天挖的土等于每天运的土解:设安排x人挖土 ,y人动土,则一天挖土5x ,一 天动土3y方所以每天安排18人挖土,30 人运土正好能使挖的土及时运走五、配套与物质分配问题例1.用白钢铁皮做头,每张铁皮可做盒身25 个,或做盒底40个,一个盒身与两个盒 底配成一套,现有36张白铁皮,用多少张做盒 身,多少张做盒 底,可使盒 身与盒 底正好配套?解:设用x张白铁皮做盒身,用y张制盒底,则共制盒身25x个,共制盒底40y个.所以用16张制盒 身,20张制盒 底正好使盒身与盒底配套例2.一张方桌由1 个桌面、4条桌腿组成,如果1立方米木料可以做方桌的桌面50个,或桌腿300条,现有5立方米的木料,那么用多少立方米木料做桌面、多少立方米木料做桌腿,做出的桌面和桌腿恰好配成方桌?能配成 多少方桌?解:设用x立方米做桌面,y立方米做桌腿,则可以做桌面50x个,做桌腿300y条所以用3立方米做桌面 ,2立方米做桌腿,恰能配成方桌,共可做成150张方桌。例3.某车间每天能生产甲种零件120个,或者乙种零件100个,或者丙种零件200个,甲,乙,丙3种零件分别取3个,2个,1个,才能配一套,要在30天内生产最多的成套产品,问甲,乙,丙3种零件各应生产多少天?六、比例问题例1.现有甲乙两种金属的合金10kg,如果加入甲种金属若干千克,那么这块金属中乙种金属占2份,甲种金属占3份;如果加入的甲的金属增加1倍,那么合金中乙种金属占3份,甲种金属占7份,问第一次加入的甲种金属有多少?原来这块合金种含甲种金属的百分比是多少 ?解:设原来这块合金中含甲金属xkg,这块合金中含乙种金属(10-x)kg,第一次加入的甲种金属ykg.根据题意,得所以第一次加入 的金属5kg,原来这块合金中含种甲金属40%甲对乙说:“当我的岁数是你现在的岁数时,你才4岁.”乙对甲说:“当我的岁数是你现在的岁数时,你将61岁.”问甲、乙现在各多少岁?从问题情境可以知知道甲的年龄大于乙的年龄解:设甲、乙现在的年龄分别是x、y岁根据题意,得答:甲、乙现在的年龄分别是42、23岁x-yX+(x-y)61Y-(x-y)42.中考链接
随着我国人口增长速度的减慢,初中入学学生数量每年按逐渐减少的趋势发展。某区2003年和2004年初中入学学生人数之比是8:7,且2003年入学人数的2倍比2004年入学人数的3倍少1500人,某人估计2005年入学学生人数将超过2300人,请你通过计算,判断他的估计是否符合当前的变化趋势。探究1
养牛场原有30只母牛和15只小牛,1天约需用饲料675kg;一周后又购进12支母牛和5只小牛,这时一天约需用饲料940kg。饲养员李大叔估计平均每只母牛1天约需饲料18-20kg,每只小牛1天约需饲料7-8kg, 你能否通过计算检验他的估计?解:设:
(相等关系)
列
解得:
答:平均每只母牛1天约需饲料xkg,每只小牛1天约需饲料ykg,
平均每只母牛1天约需饲料20kg,每只小牛1天约需饲料5kg,
李大叔对母牛的估计较准确,对小牛的估计偏高。探究二
据以往统计资料,甲,乙两种作物的单位面积产量的比是1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲,乙两种作物的总产量的比是3:4(结果取整数)?3。开放性问题
联想集团有A型、B型、C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元,我市某中学计划将100500元钱全部用于购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案,并说明理由。反思:未知数不只两个,为了解决问题方便,所以设三个未知数以帮助解决问题,把问题割裂开来看,仍属于二元一次方程组,在一个问题里面设三个未知数,这本身就是一种创造性思维。例4、用一些长短相同的小木棍按图所式,连续摆正方形或六边形要求每两个相邻的图形只有一条公共边。已知摆放的正方形比六边形多4个,并且一共用了110个小木棍,问连续摆放了正方形和六边形各多少个?……一个两位数的十位数字与个位数字的和是7,如果这个两位数加上45,则恰好成为个位数字与十位数字对调后组成的两位数,求这个两位数。
一辆汽车从甲地驶往乙地,途中要过一桥。用相同时间,若车速每小时60千米,就能越过桥2千米;若车速每小时50千米,就差3千米才到桥。问甲地与桥相距多远?用了多长时间?
x Km/h、y Km/h根据题意,得5y=6x若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.4y=4x+40解之得答:甲乙两车的速度分别为50km、60km例2.一列快车长230米,一列慢车长220米,若两车同向而行,快车从追上慢车时开始到离开慢车,需90秒钟;若两车相向而行,快车从与慢车相遇时到离开慢车,只需18秒钟,问快车和慢车的速度各是多少?快车长230米,慢车长220米,若两车同向而行,快车从追上慢车时开始到离开慢车,需90秒钟乙若两车相向而行,快车从与慢车相遇时到离开慢车,只需18秒钟18(x+y)=450解之得答:快车、慢车的速度分别为15m/s、10m/s例3.甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次;如果同向出发,每隔10min相遇一次,假定两人速度不变,且甲快乙慢,求甲、乙两人的速度.甲、乙两人在周长为400m的环形跑道上练跑,如果相向出发,每隔2.5min相遇一次甲、乙两人在周长为400m的环形跑道上练跑,如果同向出发,每隔10min相遇一次10(X-Y)=400解之得答:甲乙两人的速度分别为100m/min、60m/min环形跑道追及问题等同于异地追及问题例4.已知A、B两码头之间的距离为240km,一艏船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.练习.一辆汽车从甲地驶往乙地,途中要过一桥。用相同时间,若车速每小时60千米,就能越过桥2千米;若车速每小时50千米,就差3千米才到桥。问甲地与桥相距多远?用了多长时间?轮船航向船在逆水中的速度=船在
静水中的速度-水流的速度船在顺水中的速度=船在
静水中的速度+水流的速度例5.已知A、B两码头之间的距离为240km,一艏船航行于A、B两码头之间,顺流航行需4小时 ;逆流航行时需6小时, 求船在静水中的速度及水流的速度.解:设船在静水中的速度及水流的速度分别为xkm/h、ykm/h,根据题意,得答:船在静水中的速度及水流的速度分别为50km/h、10km/h二、工程问题 工作量=工作时间×工作效率 工作效率=工作量/工作时间、工作时间=工作量/工作效率 例1.某工人原计划在限定时间内加工一批零件.如果每小时加工10个零件,就可以超额完成3 个;如果每小时加工11个零件就可以提前1h完成.问这批零件有多少个?按原计划需多少小时 完成?解:设这批零件有x个,按原计划需y小时完成,根据题意,得答:这批零件有77个,按计划需8 小时完成例2.甲乙两家服装厂生产同一规格的上衣和裤子,甲厂每月(按30天计算)用16天生产上衣,14天做裤子,共生产448套衣服(每套上、下衣各一件);乙厂每月用12天生产上衣,18天生产裤子,共生产720套衣服,两厂合并后,每月按现有能力最多能生产多少套衣服?填写下表16144481218720解:设该厂用x天生产上衣,y天生产裤子,则共生产( )x套衣服,由题意得448/16+720/12X+y=30(448/16+720/12)x=(448/14+720/18)y所以88x=88·13.5=1188三、商品经济问题本息和=本金+利息利息=本金×年利率×期数×利息税利息所得税=利息金额×20℅例1李明以两种形式分别储蓄了2000元和1000元,一年后全部取出,扣除利息所得税后可得利息43.92元,已知这两种储蓄的年利率的和为3.24℅,问这两种储蓄的年利率各是几分之几?(注:公民应交利息所得税=利息金额×20℅)解:设这两种储蓄的年利率分别是x、y,根据题意得答:这两种储蓄的年利蓄分别为2.25%、0.09%例2。某超市在“五一”期间寻顾客实行优惠,规定如下:(2)若顾客在该超市一次性购物 x元,当小于500元但不小于200元时,他实际付款 元;当x大于或等于500元时,他实际付款 元(用的代数式表示)(1)王老师一次购物600元,他实际付款 元 5300.9x0.8x+50解:设第一次购物的货款为x元,第二次购物的货款为y元①当x<200,则,y≥500,由题意得②当x小于500元但不小于200元时,y ≥ 500,由题意得③当均小于500元但不小于200元时,且,由题意 得综上所述,两次购物的分别为110元、710元或220元、600元此方程组无解.四、配套问题(一)配套与人员分配问题例1.某车间22名工人生产螺钉与螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母,为了使每天生产的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?一个螺钉配两个螺母螺钉数:螺母数=1:2解:设分配名x工人生产螺钉,y名工人生产螺母,则一天生产的螺钉数为1200x个,生产的螺母数为2000y个.所以为了使每天生产的产品刚好配套,应安排10人生产螺钉,12人生产螺母例2.某工地需雪派48人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应该怎样安排人员,正好能使挖的土能及时运走?每天挖的土等于每天运的土解:设安排x人挖土 ,y人动土,则一天挖土5x ,一 天动土3y方所以每天安排18人挖土,30 人运土正好能使挖的土及时运走五、配套与物质分配问题例1.用白钢铁皮做头,每张铁皮可做盒身25 个,或做盒底40个,一个盒身与两个盒 底配成一套,现有36张白铁皮,用多少张做盒 身,多少张做盒 底,可使盒 身与盒 底正好配套?解:设用x张白铁皮做盒身,用y张制盒底,则共制盒身25x个,共制盒底40y个.所以用16张制盒 身,20张制盒 底正好使盒身与盒底配套例2.一张方桌由1 个桌面、4条桌腿组成,如果1立方米木料可以做方桌的桌面50个,或桌腿300条,现有5立方米的木料,那么用多少立方米木料做桌面、多少立方米木料做桌腿,做出的桌面和桌腿恰好配成方桌?能配成 多少方桌?解:设用x立方米做桌面,y立方米做桌腿,则可以做桌面50x个,做桌腿300y条所以用3立方米做桌面 ,2立方米做桌腿,恰能配成方桌,共可做成150张方桌。例3.某车间每天能生产甲种零件120个,或者乙种零件100个,或者丙种零件200个,甲,乙,丙3种零件分别取3个,2个,1个,才能配一套,要在30天内生产最多的成套产品,问甲,乙,丙3种零件各应生产多少天?六、比例问题例1.现有甲乙两种金属的合金10kg,如果加入甲种金属若干千克,那么这块金属中乙种金属占2份,甲种金属占3份;如果加入的甲的金属增加1倍,那么合金中乙种金属占3份,甲种金属占7份,问第一次加入的甲种金属有多少?原来这块合金种含甲种金属的百分比是多少 ?解:设原来这块合金中含甲金属xkg,这块合金中含乙种金属(10-x)kg,第一次加入的甲种金属ykg.根据题意,得所以第一次加入 的金属5kg,原来这块合金中含种甲金属40%甲对乙说:“当我的岁数是你现在的岁数时,你才4岁.”乙对甲说:“当我的岁数是你现在的岁数时,你将61岁.”问甲、乙现在各多少岁?从问题情境可以知知道甲的年龄大于乙的年龄解:设甲、乙现在的年龄分别是x、y岁根据题意,得答:甲、乙现在的年龄分别是42、23岁x-yX+(x-y)61Y-(x-y)42.中考链接
随着我国人口增长速度的减慢,初中入学学生数量每年按逐渐减少的趋势发展。某区2003年和2004年初中入学学生人数之比是8:7,且2003年入学人数的2倍比2004年入学人数的3倍少1500人,某人估计2005年入学学生人数将超过2300人,请你通过计算,判断他的估计是否符合当前的变化趋势。探究1
养牛场原有30只母牛和15只小牛,1天约需用饲料675kg;一周后又购进12支母牛和5只小牛,这时一天约需用饲料940kg。饲养员李大叔估计平均每只母牛1天约需饲料18-20kg,每只小牛1天约需饲料7-8kg, 你能否通过计算检验他的估计?解:设:
(相等关系)
列
解得:
答:平均每只母牛1天约需饲料xkg,每只小牛1天约需饲料ykg,
平均每只母牛1天约需饲料20kg,每只小牛1天约需饲料5kg,
李大叔对母牛的估计较准确,对小牛的估计偏高。探究二
据以往统计资料,甲,乙两种作物的单位面积产量的比是1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲,乙两种作物的总产量的比是3:4(结果取整数)?3。开放性问题
联想集团有A型、B型、C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元,我市某中学计划将100500元钱全部用于购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案,并说明理由。反思:未知数不只两个,为了解决问题方便,所以设三个未知数以帮助解决问题,把问题割裂开来看,仍属于二元一次方程组,在一个问题里面设三个未知数,这本身就是一种创造性思维。例4、用一些长短相同的小木棍按图所式,连续摆正方形或六边形要求每两个相邻的图形只有一条公共边。已知摆放的正方形比六边形多4个,并且一共用了110个小木棍,问连续摆放了正方形和六边形各多少个?……一个两位数的十位数字与个位数字的和是7,如果这个两位数加上45,则恰好成为个位数字与十位数字对调后组成的两位数,求这个两位数。
一辆汽车从甲地驶往乙地,途中要过一桥。用相同时间,若车速每小时60千米,就能越过桥2千米;若车速每小时50千米,就差3千米才到桥。问甲地与桥相距多远?用了多长时间?
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
