北师大版数学七年级上册 3.5探索与表达规律 课后练习 (含解析)
文档属性
| 名称 | 北师大版数学七年级上册 3.5探索与表达规律 课后练习 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 10:30:38 | ||
图片预览



文档简介
探索与表达规律
一.选择题
1.按照一定规律排列的式子:,,,,则第7个式子是
A. B. C. D.
2.将连续正整数按如图所示的位置顺序排列,根据排列规律,则2023应在
A.处 B.处 C.处 D.处
3.有一列按规律排列的数:,9,,81,,729,,则第个数是
A. B. C. D.
4.如图所示,将部分偶数依顺序排列成三角形数阵,从上到下称为行.图中数6为第2行、从左向右第2个数;数为第4行、从左向右第3个数,那么第11行、从左向右第5个数为
A.210 B.230 C. D.
5.若2023个数、、、、满足下列条件:,,,,,则
A.2 B. C. D.
6.计算的值等于
A. B. C.1012 D.1013
7.若是不为2的有理数,则我们把称为的“哈利数”.如:3的“哈利数”是,的“哈利数”是.已知,是的“哈利数”, 是的“哈利数”, 是的“哈利数”, ,以此类推,则等于
A.3 B. C. D.
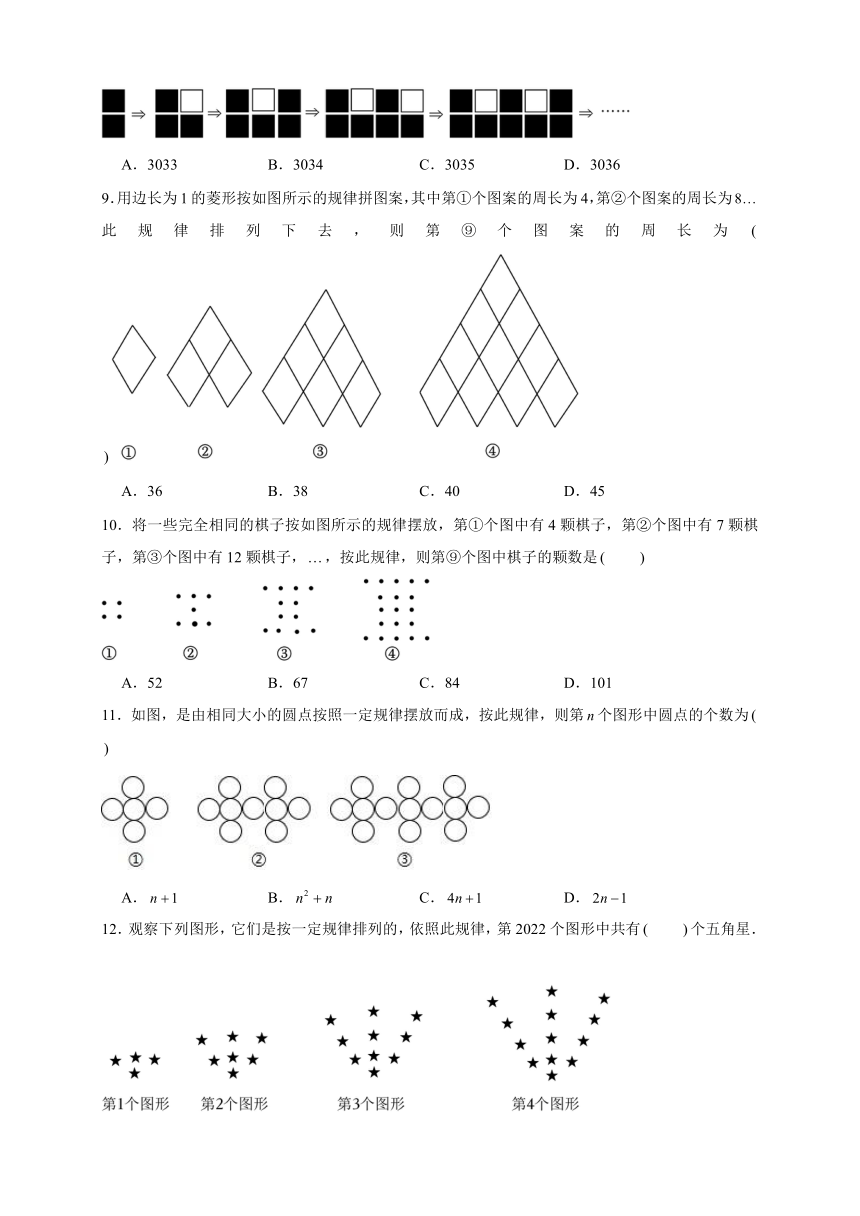
8.找出以下图形变化的规律,则第2023个图形中黑色正方形的数量是
A.3033 B.3034 C.3035 D.3036
9.用边长为1的菱形按如图所示的规律拼图案,其中第①个图案的周长为4,第②个图案的周长为此规律排列下去,则第⑨个图案的周长为
A.36 B.38 C.40 D.45
10.将一些完全相同的棋子按如图所示的规律摆放,第①个图中有4颗棋子,第②个图中有7颗棋子,第③个图中有12颗棋子,,按此规律,则第⑨个图中棋子的颗数是
A.52 B.67 C.84 D.101
11.如图,是由相同大小的圆点按照一定规律摆放而成,按此规律,则第个图形中圆点的个数为
A. B. C. D.
12.观察下列图形,它们是按一定规律排列的,依照此规律,第2022个图形中共有 个五角星.
A.6068 B.6067 C.6066 D.6065
二.填空题
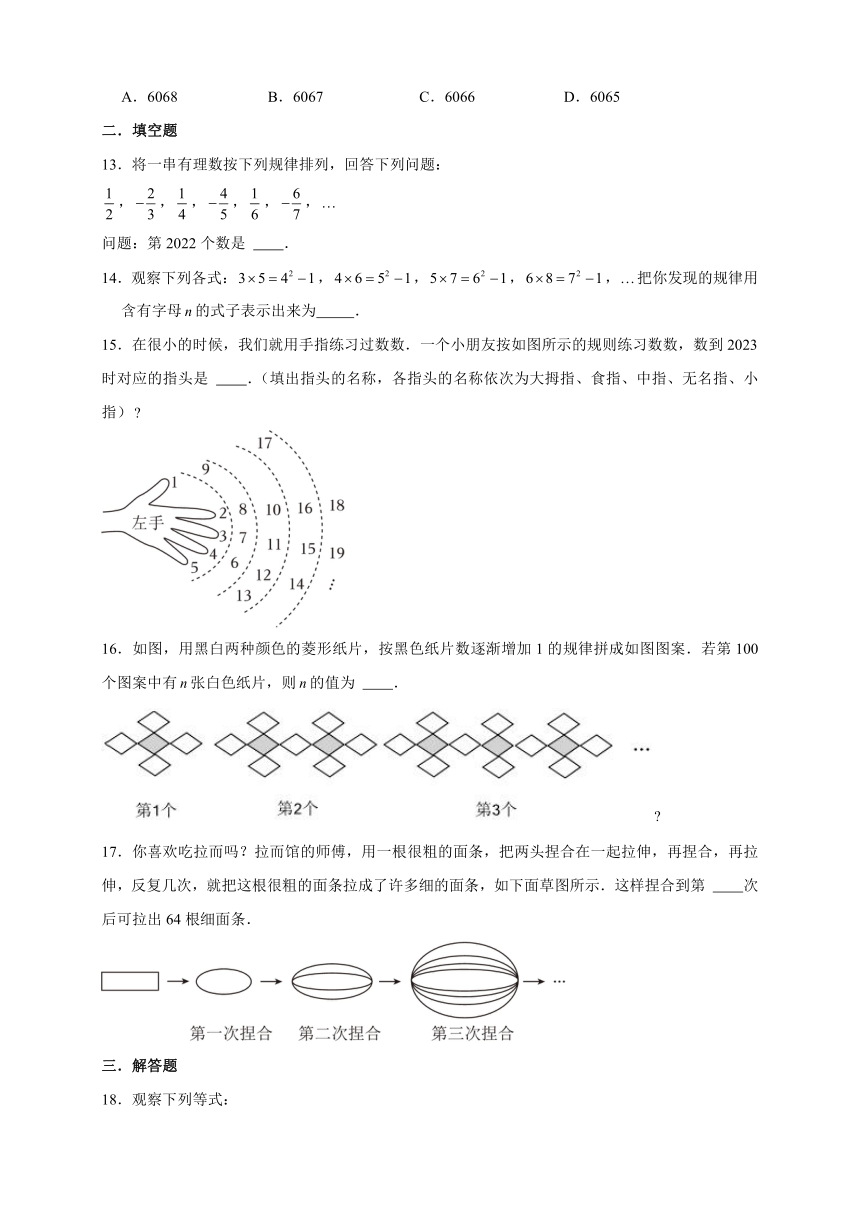
13.将一串有理数按下列规律排列,回答下列问题:
,,,,,,
问题:第2022个数是 .
14.观察下列各式:,,,,把你发现的规律用含有字母的式子表示出来为 .
15.在很小的时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2023时对应的指头是 .(填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指)
16.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成如图图案.若第100个图案中有张白色纸片,则的值为 .
17.你喜欢吃拉而吗?拉而馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示.这样捏合到第 次后可拉出64根细面条.
三.解答题
18.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
请回答下列问题:
(1)按以上规律写出第5个等式:
;
(2)求的值.
19.探索规律:观察下面※由组成的图案和算式,解答问题:
(1)请猜想 ;
(2)请猜想 ;
(3)请用上述规律计算:的值.
20.观察下面三行数:
,4,,16,,64,;①
,5,,17,,65,;②
0,3,,9,,33,;③
(1)第①行的第9个数是 ,第①行第个数是 (用的式子表示);
(2)设第①行第个数为,用含的式子表示第②,③行数的第个数;
(3)取第①,②,③行的第100个数分别记为,,,求的值.
21.【观察思考】
【规律发现】
(1)第5个图案中“★”的个数是 .
(2)第5个图案中“◎”的个数是 ;第2023个图案中“◎”的个数是 .
【猜想说理】
(3)有人猜想:当是正整数时,第个图案与第个图案中“★”的个数之差为.你同意他的说法吗?请写出理由.
22.阅读材料:课堂上,老师在黑板上讲解了以下两道题:
问题1:计算:. 解:. 这个问题采用了乘法的分配律. 问题2:计算. 解:原式. 这个问题采用了乘法的交换律和结合律.
尝试解决:(1)计算:.
应用解决:(2)将24减去它的,再减去余下的,再减去余下的,,依次类推,直到减去余下的,最后的结果是多少?
(3)已知有理数,把叫做的差倒数,如的差倒数为的差倒数为,若,的差倒数为,的差倒数为,的差倒数为,,依次类推,求的值.
参考答案
1.
解:,
,
,
第7个式子是:,
故选:.
2.
解:,
应在3的位置,也就是在处.
故选:.
3.
解:根据所给数列可知,
后一个数是前一个数的倍,
又第一个数是,
所以第个数是.
故选:.
4.
解:观察所给数列可知,
所有数的绝对值是从2开始的连续偶数,
且第行有个数,
所以前10行一共有个数,
又从2开始的第100个偶数是200,
即第10行最后一个数的绝对值是200.
所以第11行第一个数的绝对值是202,
又奇数行第一个数为正,偶数行第一个数为负,
且所有行都为正负数相间排列,
所以第11行、从左向右第5个数为:210.
故选:.
5.
解:因为,
所以,
,
,
,
,
因为,
,
则,
故选:.
6.
解:
,
故选:.
7.
解:,
,
,
,
,
该数列每4个数为1周期循环,
,
.
故选:.
8.
解:根据图形变化规律可知:
第1个图形中黑色正方形的数量为2,
第2个图形中黑色正方形的数量为3,
第3个图形中黑色正方形的数量为5,
第4个图形中黑色正方形的数量为6,
,
当为奇数时,黑色正方形的个数为,
当为偶数时,黑色正方形的个数为,
第2023个图形中黑色正方形的数量是,
故选:.
9.
解:第①个图案的周长为,
第②个图案的周长为,
第③个图案的周长为,
第④个图案的周长为,
,
此规律排列下去,则第⑨个图案的周长为,
故选:.
10.
解:第①个图形中,棋子数量为;
第②个图形中,棋子数量为;
第③个图形中,棋子数量为;
以此类推,
第个图形中,棋子数量为;
第⑨个图形中共有棋子的颗数是,
故选:.
11.解:观察图形的变化可知:
第1个图形中圆点的个数为;
第2个图形中圆点的个数为;
第3个图形中圆点的个数为;
发现规律,
则第个图形中圆点的个数为.
故选:.
12.
解:第一个图形五角星数目:,
第二个图形五角星数目:,
第三个图形五角星数目:,
第四个图形五角星数目:,
第个图形五角星数目:,
第2022个图形中五角星数目为:.
故选:.
13..
解:一串有理数为:,,,,,,,
这列数的第个数的分母是,当为奇数时,分子是1,当为偶数时,分子是,
第2022个数是,
故答案为:.
14.解:,,,,
规律为:.
故答案为:.
15.中指.
解:根据题意,大拇指上的数据为:1,9,17,都是8的倍数加1,
,
在大拇指上,
倒推2023在中指位置.
故答案为:中指.
16.301.
解:第1个图案中有个白色纸片,
第2个图案中有个白色纸片,
第3个图案中有个白色纸片,
,
第个图案中有个白色纸片,
当时,,
故答案为:301.
17.6.
解:根据所给图形可知,
捏合1次可拉出面条的根数为:;
捏合2次可拉出的面条根数为:;
捏合3次可拉出的面条根数为:;
所以捏合次可拉出的面条根数为:(根.
令得,
,
所以捏合到第6次可拉出64根细面条.
故答案为:6.
18..
解:(1),
故答案为:,;
(2)
.
19.(1)100;(2);(3)9100.
解:(1)由图得:,1有1项;
,有2项;
,有3项;
,有4项;
,有5项;
共有项,
,
故答案为:100;
(2),
,
故答案为:;
(3)当时,,当时,
.
20.(1),;
(2)第②行的第100个数是,第③行的第100个数是;
(3).
解:(1)观察第①行数可知,
后一个数是前一个数的倍,且第一个数是,
所以第①行的第9个数是,
第①行的第个数是.
故答案为:,.
(2)观察第①②两行数可知,
第②行的第个数比第①行的第个数大1,
所以第②行的第个数是:.
观察第②③两行数可知,
第③行的第个数比第②行的第个数大,
所以第③行的第个数是:.
(3)第①行的第100个数为:,
即.
第②行的第100个数为:,
即.
第③行的第100个数为:,
即.
所以
.
21.(1)15;
(2)15,6069;
(3)同意,见解答过程.
解:(1)第1个图案中“★”的个数是:1,
第2个图案中“★”的个数是:,
第3个图案中“★”的个数是:,
,
第个图案中“★”的个数是:,
第5个图案中“★”的个数是:,
故答案为:15;
(2)第1个图案中“◎”的个数是:3
第2个图案中“◎”的个数是:,
第5个图案中“◎”的个数是:,
,
第个图案中“◎”的个数是:,
第5个图案中“◎”的个数是:,
第2023个图案中“◎”的个数是:,
故答案为:15,6069;
(3)同意,理由如下:
第个图案中“★”的个数是:,
则
.
22.(1)9900;
(2)1;
(3).
解:(1)原式
;
(2)由题意,列式如下:
;
(3),的差倒数为,的差倒数为,的差倒数为,,
,,,
每3个差倒数一循环,
,,,
.
一.选择题
1.按照一定规律排列的式子:,,,,则第7个式子是
A. B. C. D.
2.将连续正整数按如图所示的位置顺序排列,根据排列规律,则2023应在
A.处 B.处 C.处 D.处
3.有一列按规律排列的数:,9,,81,,729,,则第个数是
A. B. C. D.
4.如图所示,将部分偶数依顺序排列成三角形数阵,从上到下称为行.图中数6为第2行、从左向右第2个数;数为第4行、从左向右第3个数,那么第11行、从左向右第5个数为
A.210 B.230 C. D.
5.若2023个数、、、、满足下列条件:,,,,,则
A.2 B. C. D.
6.计算的值等于
A. B. C.1012 D.1013
7.若是不为2的有理数,则我们把称为的“哈利数”.如:3的“哈利数”是,的“哈利数”是.已知,是的“哈利数”, 是的“哈利数”, 是的“哈利数”, ,以此类推,则等于
A.3 B. C. D.
8.找出以下图形变化的规律,则第2023个图形中黑色正方形的数量是
A.3033 B.3034 C.3035 D.3036
9.用边长为1的菱形按如图所示的规律拼图案,其中第①个图案的周长为4,第②个图案的周长为此规律排列下去,则第⑨个图案的周长为
A.36 B.38 C.40 D.45
10.将一些完全相同的棋子按如图所示的规律摆放,第①个图中有4颗棋子,第②个图中有7颗棋子,第③个图中有12颗棋子,,按此规律,则第⑨个图中棋子的颗数是
A.52 B.67 C.84 D.101
11.如图,是由相同大小的圆点按照一定规律摆放而成,按此规律,则第个图形中圆点的个数为
A. B. C. D.
12.观察下列图形,它们是按一定规律排列的,依照此规律,第2022个图形中共有 个五角星.
A.6068 B.6067 C.6066 D.6065
二.填空题
13.将一串有理数按下列规律排列,回答下列问题:
,,,,,,
问题:第2022个数是 .
14.观察下列各式:,,,,把你发现的规律用含有字母的式子表示出来为 .
15.在很小的时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2023时对应的指头是 .(填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指)
16.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成如图图案.若第100个图案中有张白色纸片,则的值为 .
17.你喜欢吃拉而吗?拉而馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示.这样捏合到第 次后可拉出64根细面条.
三.解答题
18.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
请回答下列问题:
(1)按以上规律写出第5个等式:
;
(2)求的值.
19.探索规律:观察下面※由组成的图案和算式,解答问题:
(1)请猜想 ;
(2)请猜想 ;
(3)请用上述规律计算:的值.
20.观察下面三行数:
,4,,16,,64,;①
,5,,17,,65,;②
0,3,,9,,33,;③
(1)第①行的第9个数是 ,第①行第个数是 (用的式子表示);
(2)设第①行第个数为,用含的式子表示第②,③行数的第个数;
(3)取第①,②,③行的第100个数分别记为,,,求的值.
21.【观察思考】
【规律发现】
(1)第5个图案中“★”的个数是 .
(2)第5个图案中“◎”的个数是 ;第2023个图案中“◎”的个数是 .
【猜想说理】
(3)有人猜想:当是正整数时,第个图案与第个图案中“★”的个数之差为.你同意他的说法吗?请写出理由.
22.阅读材料:课堂上,老师在黑板上讲解了以下两道题:
问题1:计算:. 解:. 这个问题采用了乘法的分配律. 问题2:计算. 解:原式. 这个问题采用了乘法的交换律和结合律.
尝试解决:(1)计算:.
应用解决:(2)将24减去它的,再减去余下的,再减去余下的,,依次类推,直到减去余下的,最后的结果是多少?
(3)已知有理数,把叫做的差倒数,如的差倒数为的差倒数为,若,的差倒数为,的差倒数为,的差倒数为,,依次类推,求的值.
参考答案
1.
解:,
,
,
第7个式子是:,
故选:.
2.
解:,
应在3的位置,也就是在处.
故选:.
3.
解:根据所给数列可知,
后一个数是前一个数的倍,
又第一个数是,
所以第个数是.
故选:.
4.
解:观察所给数列可知,
所有数的绝对值是从2开始的连续偶数,
且第行有个数,
所以前10行一共有个数,
又从2开始的第100个偶数是200,
即第10行最后一个数的绝对值是200.
所以第11行第一个数的绝对值是202,
又奇数行第一个数为正,偶数行第一个数为负,
且所有行都为正负数相间排列,
所以第11行、从左向右第5个数为:210.
故选:.
5.
解:因为,
所以,
,
,
,
,
因为,
,
则,
故选:.
6.
解:
,
故选:.
7.
解:,
,
,
,
,
该数列每4个数为1周期循环,
,
.
故选:.
8.
解:根据图形变化规律可知:
第1个图形中黑色正方形的数量为2,
第2个图形中黑色正方形的数量为3,
第3个图形中黑色正方形的数量为5,
第4个图形中黑色正方形的数量为6,
,
当为奇数时,黑色正方形的个数为,
当为偶数时,黑色正方形的个数为,
第2023个图形中黑色正方形的数量是,
故选:.
9.
解:第①个图案的周长为,
第②个图案的周长为,
第③个图案的周长为,
第④个图案的周长为,
,
此规律排列下去,则第⑨个图案的周长为,
故选:.
10.
解:第①个图形中,棋子数量为;
第②个图形中,棋子数量为;
第③个图形中,棋子数量为;
以此类推,
第个图形中,棋子数量为;
第⑨个图形中共有棋子的颗数是,
故选:.
11.解:观察图形的变化可知:
第1个图形中圆点的个数为;
第2个图形中圆点的个数为;
第3个图形中圆点的个数为;
发现规律,
则第个图形中圆点的个数为.
故选:.
12.
解:第一个图形五角星数目:,
第二个图形五角星数目:,
第三个图形五角星数目:,
第四个图形五角星数目:,
第个图形五角星数目:,
第2022个图形中五角星数目为:.
故选:.
13..
解:一串有理数为:,,,,,,,
这列数的第个数的分母是,当为奇数时,分子是1,当为偶数时,分子是,
第2022个数是,
故答案为:.
14.解:,,,,
规律为:.
故答案为:.
15.中指.
解:根据题意,大拇指上的数据为:1,9,17,都是8的倍数加1,
,
在大拇指上,
倒推2023在中指位置.
故答案为:中指.
16.301.
解:第1个图案中有个白色纸片,
第2个图案中有个白色纸片,
第3个图案中有个白色纸片,
,
第个图案中有个白色纸片,
当时,,
故答案为:301.
17.6.
解:根据所给图形可知,
捏合1次可拉出面条的根数为:;
捏合2次可拉出的面条根数为:;
捏合3次可拉出的面条根数为:;
所以捏合次可拉出的面条根数为:(根.
令得,
,
所以捏合到第6次可拉出64根细面条.
故答案为:6.
18..
解:(1),
故答案为:,;
(2)
.
19.(1)100;(2);(3)9100.
解:(1)由图得:,1有1项;
,有2项;
,有3项;
,有4项;
,有5项;
共有项,
,
故答案为:100;
(2),
,
故答案为:;
(3)当时,,当时,
.
20.(1),;
(2)第②行的第100个数是,第③行的第100个数是;
(3).
解:(1)观察第①行数可知,
后一个数是前一个数的倍,且第一个数是,
所以第①行的第9个数是,
第①行的第个数是.
故答案为:,.
(2)观察第①②两行数可知,
第②行的第个数比第①行的第个数大1,
所以第②行的第个数是:.
观察第②③两行数可知,
第③行的第个数比第②行的第个数大,
所以第③行的第个数是:.
(3)第①行的第100个数为:,
即.
第②行的第100个数为:,
即.
第③行的第100个数为:,
即.
所以
.
21.(1)15;
(2)15,6069;
(3)同意,见解答过程.
解:(1)第1个图案中“★”的个数是:1,
第2个图案中“★”的个数是:,
第3个图案中“★”的个数是:,
,
第个图案中“★”的个数是:,
第5个图案中“★”的个数是:,
故答案为:15;
(2)第1个图案中“◎”的个数是:3
第2个图案中“◎”的个数是:,
第5个图案中“◎”的个数是:,
,
第个图案中“◎”的个数是:,
第5个图案中“◎”的个数是:,
第2023个图案中“◎”的个数是:,
故答案为:15,6069;
(3)同意,理由如下:
第个图案中“★”的个数是:,
则
.
22.(1)9900;
(2)1;
(3).
解:(1)原式
;
(2)由题意,列式如下:
;
(3),的差倒数为,的差倒数为,的差倒数为,,
,,,
每3个差倒数一循环,
,,,
.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
