苏教版(2019)选择性必修第一册 2.1圆的标准方程教学 课件(共21张PPT)
文档属性
| 名称 | 苏教版(2019)选择性必修第一册 2.1圆的标准方程教学 课件(共21张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 258.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 19:06:10 | ||
图片预览








文档简介
(共21张PPT)
A
r
x
y
O
圆的标准方程
1.掌握圆的标准方程及其特点,会根据圆心的位置和半径写出圆的标准方程.
2.能运用圆的方程判断点和圆的位置关系
3.能根据某些具体条件,运用待定系数法确定圆的方程.
在前面我们学过,在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.那么在平面直角坐标系中,如何确定一个圆呢?
复习引入
问题:
1、圆的定义
平面内与定点距离等于定长的点的集合(轨迹)是圆,定点就是圆心,定长就是半径.
当圆心位置与半径大小确定后,圆就唯一确定了。 因此一个圆最基本要素是:圆心和半径.
如图,在平面直角坐标系中,圆心(点)A的位置用坐标 (a,b) 表示,半径r的大小等于圆上任意点M(x, y)与圆心A (a,b) 的距离.
x
O
y
A
(a,b)
M
r
(x, y)
符合上述条件的圆的集合是什么?你能用描述法来表示这个集合吗?
符合上述条件的圆的集合:
2、圆的方程的推导
问题三:圆心是A(a,b),半径是r的圆的方程是什么?
x
y
O
A
M(x,y)
P = { M | |MA| = r }
圆上所有点的集合
(x-a)2+(y-b)2=r2
三个独立条件a、b、r确定一个圆的方程.
设点M (x,y)为圆A上任一点,则|MA|= r。
探究新知
r
问题:是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上?
点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.
想一想
思考
x
y
O
C
M(x,y)
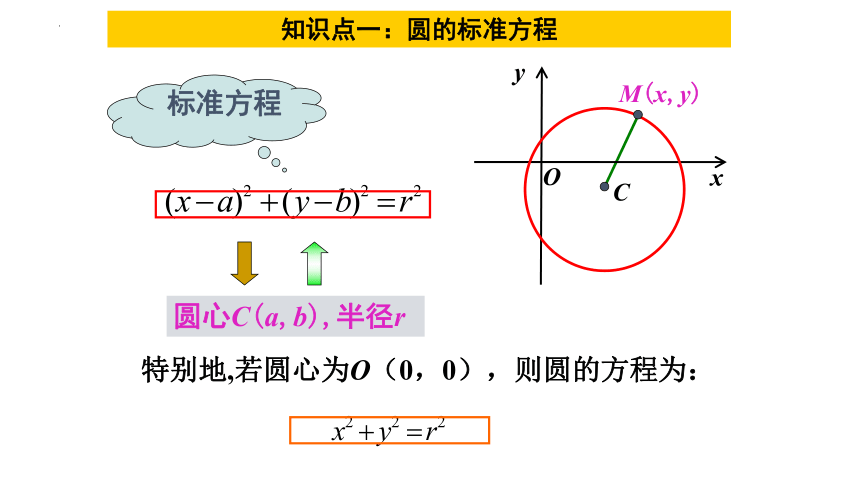
圆心C(a,b),半径r
特别地,若圆心为O(0,0),则圆的方程为:
标准方程
知识点一:圆的标准方程
知识探究二:点与圆的位置关系
探究:在平面几何中,如何确定点与圆的位置关 系?
M
O
|OM||OM|=r
O
M
O
M
|OM|>r
点在圆内
点在圆上
点在圆外
(x0-a)2+(y0-b)2>r2时,点M在圆C外;
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
(x0-a)2+(y0-b)2点与圆的位置关系:
知识点二:点与圆的位置关系
例1:求满足下列条件的圆的标准方程
(1)圆心在原点,半径为3;
(2)圆心在点(-2,1),半径为 ;
(3)经过点P(5,1),圆心在点(8,-3).
例2.圆的方程为
判断点A(5,7),点B(-5,-1)在圆上、圆内、还是圆外?
自我检测:
1.说出下面圆的圆心和半径
2.已知圆的方程为
判断下列各点在圆上、在圆内、还是在园外?
A(4,-5);B(5,1);D(3,-6)
总结:点和圆的位置关系的判断
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
例2 ⊿ABC的三个顶点的坐标分别是A(5,1),
B(7,-3),C(2,-8),求它的外接圆的方程。
圆心:两条直线的交点
半径:圆心到圆上一点
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
典型例题: 例3:己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
解:∵A(1,1),B(2,-2)
即:x-3y-3=0
∴圆心C(-3,-2)
公式法
圆经过A(1,1),B(2,-2)
解2:设圆C的方程为
∵圆心在直线l:x-y+1=0上
待定系数法
小结:
(1)、牢记: 圆的标准方程:(x-a)2+(y-b)2=r2。
(2)、掌握:①三个条件a、b、r确定一个圆。
②点与圆的位置关系。
(3)、求圆的标准方程的方法:
待定系数法 几何性质法
分层作业:
1.课本120页1,3,4.
2.课时作业
练习:圆 关于直线 对称的圆的方程是( )
B.
C.
D.
B
分析:确定圆的几何要素的是圆心位置与半径大小.与一条直线对称的两个圆半径大小不变,圆心关于直线对称,因此,只要确定圆心位置即可.
与圆心(3,- 4)关于直线 对称的点是(4,-3),于是,与已知圆关于直线 对称的圆的方程是 .选择B.
例:以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆.
圆心:已知
半径:圆心到切线的距离
解:
设所求圆的半径为r
则:
=
∴所求圆的方程为:
C
y
x
O
M
思考
例 已知圆的方程是x2 + y2 = r2,求经过圆上一 点 的切线的方程。
X
Y
0
解:
特殊位置的圆的方程:
圆心在原点:
x2 + y2 = r2 (r≠0)
圆心在x轴上:
(x a)2 + y2 = r2 (r≠0)
圆心在y轴上:
x2+ (y b)2 = r2 (r≠0)
圆过原点:
(x a)2 + (y-b)2 = b2 (b≠0)
圆心在x轴上且过原点:
(x a)2 + y2 = a2 (a≠0)
圆心在y轴上且过原点:
x 2 + (y-b)2 = b2 (b≠0)
圆与x轴相切:
(x a)2 + (y-b)2 = a2+b2 (a2+b2≠0)
圆与y轴相切:
(x a)2 + (y-b)2 = a2 (a≠0)
圆与x,y轴都相切:
(x a)2 + (y±a)2 = a2 (a≠0)
A
r
x
y
O
圆的标准方程
1.掌握圆的标准方程及其特点,会根据圆心的位置和半径写出圆的标准方程.
2.能运用圆的方程判断点和圆的位置关系
3.能根据某些具体条件,运用待定系数法确定圆的方程.
在前面我们学过,在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.那么在平面直角坐标系中,如何确定一个圆呢?
复习引入
问题:
1、圆的定义
平面内与定点距离等于定长的点的集合(轨迹)是圆,定点就是圆心,定长就是半径.
当圆心位置与半径大小确定后,圆就唯一确定了。 因此一个圆最基本要素是:圆心和半径.
如图,在平面直角坐标系中,圆心(点)A的位置用坐标 (a,b) 表示,半径r的大小等于圆上任意点M(x, y)与圆心A (a,b) 的距离.
x
O
y
A
(a,b)
M
r
(x, y)
符合上述条件的圆的集合是什么?你能用描述法来表示这个集合吗?
符合上述条件的圆的集合:
2、圆的方程的推导
问题三:圆心是A(a,b),半径是r的圆的方程是什么?
x
y
O
A
M(x,y)
P = { M | |MA| = r }
圆上所有点的集合
(x-a)2+(y-b)2=r2
三个独立条件a、b、r确定一个圆的方程.
设点M (x,y)为圆A上任一点,则|MA|= r。
探究新知
r
问题:是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上?
点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.
想一想
思考
x
y
O
C
M(x,y)
圆心C(a,b),半径r
特别地,若圆心为O(0,0),则圆的方程为:
标准方程
知识点一:圆的标准方程
知识探究二:点与圆的位置关系
探究:在平面几何中,如何确定点与圆的位置关 系?
M
O
|OM|
O
M
O
M
|OM|>r
点在圆内
点在圆上
点在圆外
(x0-a)2+(y0-b)2>r2时,点M在圆C外;
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
(x0-a)2+(y0-b)2
知识点二:点与圆的位置关系
例1:求满足下列条件的圆的标准方程
(1)圆心在原点,半径为3;
(2)圆心在点(-2,1),半径为 ;
(3)经过点P(5,1),圆心在点(8,-3).
例2.圆的方程为
判断点A(5,7),点B(-5,-1)在圆上、圆内、还是圆外?
自我检测:
1.说出下面圆的圆心和半径
2.已知圆的方程为
判断下列各点在圆上、在圆内、还是在园外?
A(4,-5);B(5,1);D(3,-6)
总结:点和圆的位置关系的判断
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
例2 ⊿ABC的三个顶点的坐标分别是A(5,1),
B(7,-3),C(2,-8),求它的外接圆的方程。
圆心:两条直线的交点
半径:圆心到圆上一点
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
典型例题: 例3:己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
解:∵A(1,1),B(2,-2)
即:x-3y-3=0
∴圆心C(-3,-2)
公式法
圆经过A(1,1),B(2,-2)
解2:设圆C的方程为
∵圆心在直线l:x-y+1=0上
待定系数法
小结:
(1)、牢记: 圆的标准方程:(x-a)2+(y-b)2=r2。
(2)、掌握:①三个条件a、b、r确定一个圆。
②点与圆的位置关系。
(3)、求圆的标准方程的方法:
待定系数法 几何性质法
分层作业:
1.课本120页1,3,4.
2.课时作业
练习:圆 关于直线 对称的圆的方程是( )
B.
C.
D.
B
分析:确定圆的几何要素的是圆心位置与半径大小.与一条直线对称的两个圆半径大小不变,圆心关于直线对称,因此,只要确定圆心位置即可.
与圆心(3,- 4)关于直线 对称的点是(4,-3),于是,与已知圆关于直线 对称的圆的方程是 .选择B.
例:以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆.
圆心:已知
半径:圆心到切线的距离
解:
设所求圆的半径为r
则:
=
∴所求圆的方程为:
C
y
x
O
M
思考
例 已知圆的方程是x2 + y2 = r2,求经过圆上一 点 的切线的方程。
X
Y
0
解:
特殊位置的圆的方程:
圆心在原点:
x2 + y2 = r2 (r≠0)
圆心在x轴上:
(x a)2 + y2 = r2 (r≠0)
圆心在y轴上:
x2+ (y b)2 = r2 (r≠0)
圆过原点:
(x a)2 + (y-b)2 = b2 (b≠0)
圆心在x轴上且过原点:
(x a)2 + y2 = a2 (a≠0)
圆心在y轴上且过原点:
x 2 + (y-b)2 = b2 (b≠0)
圆与x轴相切:
(x a)2 + (y-b)2 = a2+b2 (a2+b2≠0)
圆与y轴相切:
(x a)2 + (y-b)2 = a2 (a≠0)
圆与x,y轴都相切:
(x a)2 + (y±a)2 = a2 (a≠0)
