2015春湘教版数学八下1.4《角平分线的性质》课件4(共22张PPT)
文档属性
| 名称 | 2015春湘教版数学八下1.4《角平分线的性质》课件4(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 368.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-02 08:46:02 | ||
图片预览






文档简介
课件22张PPT。1.4角平分线的性质 1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理:
在一个角的内部,到一个角的两边的距离相等的点,在这个角平分线上。
4.角平分线的性质定理是证明角相等、线段相等的新途径.角平分线的逆定理是证明点在直线上(或直线经过某一点)的根据之一.3.性质定理和逆定理的关系
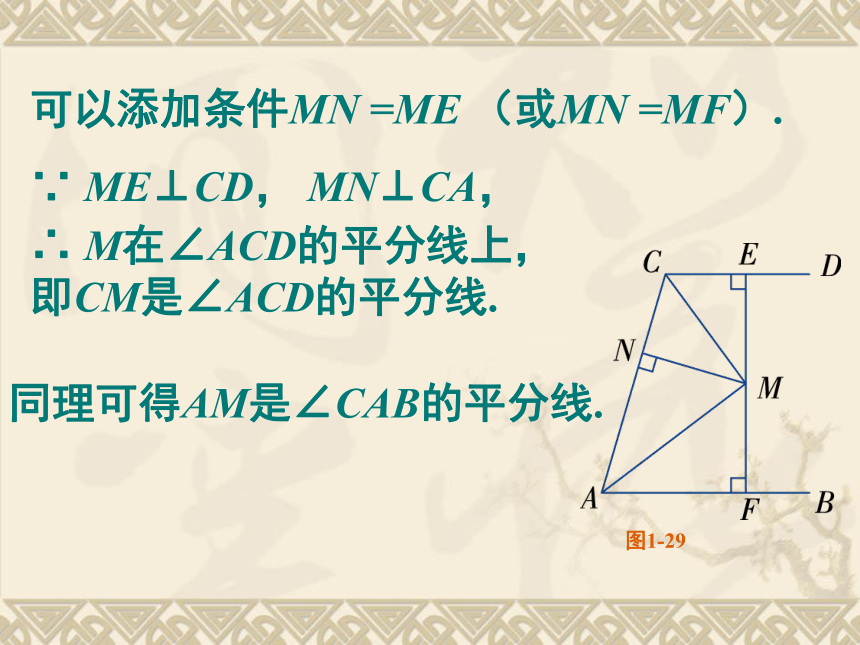
点在角平分线上 点到角两边的距离相等回顾: 如图1-29, 已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF 的中点. 需添加一个什么条件, 就可使CM,AM分别为∠ACD和∠CAB的平分线呢?图1-29∵ ME⊥CD, MN⊥CA,同理可得AM是∠CAB的平分线.可以添加条件MN =ME (或MN =MF).∴ M在∠ACD的平分线上,
即CM是∠ACD的平分线.图1-29∴ PE=PF.在△EBP中,BE+PE>PB,∴ BE+PF>PB.图1-30举例三.尺规作图 角平分线的作法已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC
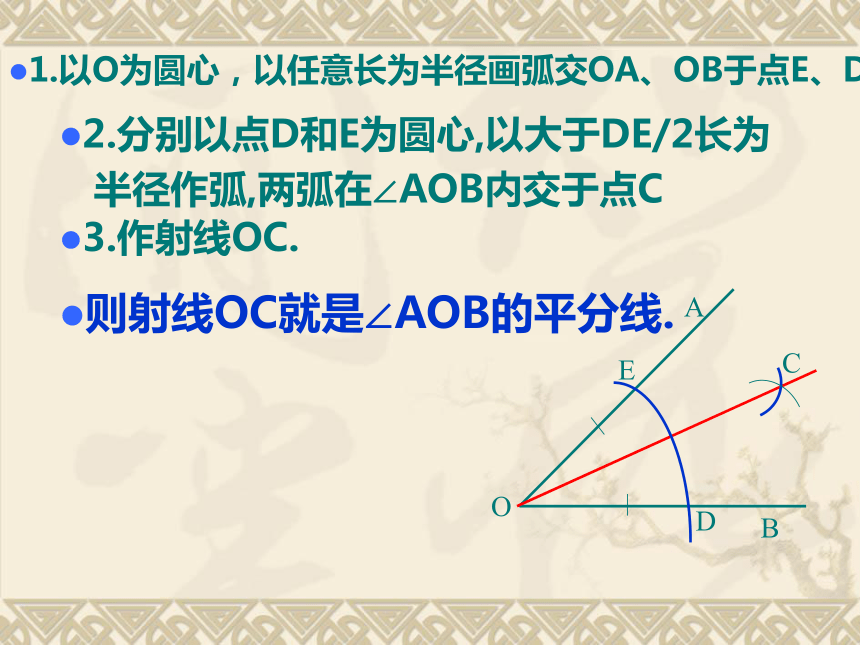
作法:用尺规作角的平分线.1.以O为圆心,以任意长为半径画弧交OA、OB于点E、D2.分别以点D和E为圆心,以大于DE/2长为
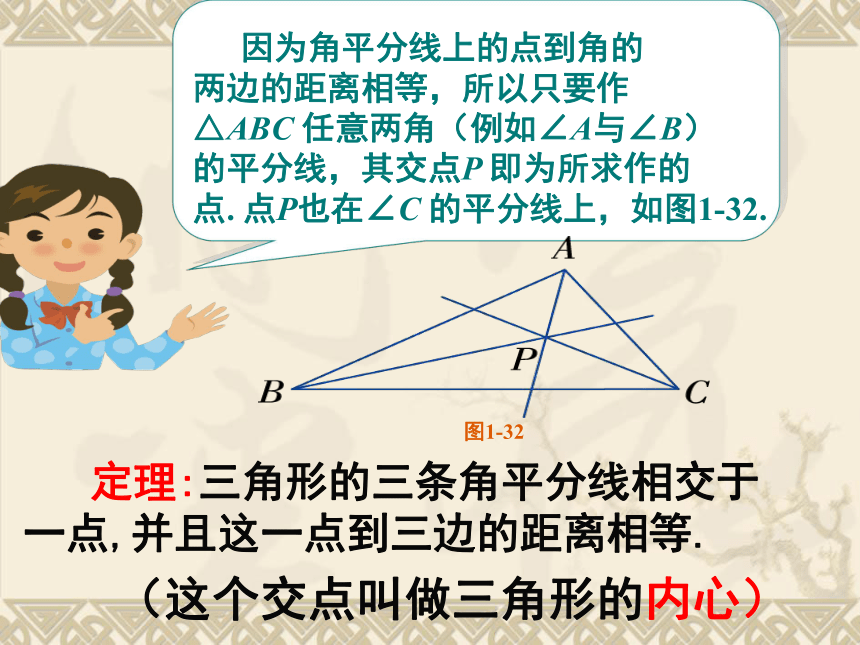
半径作弧,两弧在∠AOB内交于点C3.作射线OC.则射线OC就是∠AOB的平分线. 如图1-31,你能在△ABC 中找到一点P,使其到三边的距离相等吗?图1-31图1-32 定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等. (这个交点叫做三角形的内心)如图,E 是∠AOB 的平分线上一点,EC⊥OA 于点C,ED⊥OB 于点D.
求证:(1)∠ECD=∠EDC; (2)OC=OD.2. 如图,在△ABC 中,AD⊥DE,BE⊥DE,AC,BC 分别平分∠BAD,∠ABE,点C在线段DE上.
求证:AB=AD+BE.M证明 作CM⊥AB于点M. ∵ AC,BC 分别平分∠BAD,∠ABE,
∴ CD = CM,CE = CM.
在Rt△ACD和Rt△ACM中,
∵ CM = CD,AC = AC,
∴ Rt△ACD ≌Rt△ACM.
∴ AD = AM.
.
同理, BE = BM.
又 AB=AM+BM,∴AB=AD+BE
挑战自我基本应用填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)∠1=∠2
DC=DE到一个角的两边的距离相等的点,在这个角平分线上。在角平分线上的点到角的两边的距离相等 1.如图,AD,AE分别是△ABC中∠A的内角平 分线和外角平分线,它们有什么关系?2. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等. 3.已知:如图,∠C=900, ∠B=300, AD是Rt△ABC的角平分线.
求证:BD=2CD. 1、如图,在△ABC中,已知 AC=BC,∠C=900,AD是△ABC的角平线,DE⊥AB,垂足为E.(1)如果CD=4cm, 求AC的长;(2)求证:AB=AC+CD.延伸训练2: 已知:如图所示:PA,PC分别是⊿ABC外角∠MAC与∠NCA平分线,它们交于P,PD⊥BM于M,PF⊥BN于F
求证: 点P在∠MBN的平分线上E3、已知:如图,∠B= ∠C=90°,M是
BC的中点,DM平分∠ ADC
求证:AM平分∠DAB。 E4、已知:△MON中,MP平分∠OMN,OP平分∠MON,且PD⊥MN,PE⊥ON,垂足分别为点D、E
求证:点P在∠MNO的平分线上小结:1.定理:
角平分线上的点到这个角的两边距离相等.2.逆定理 :
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.3.定理:三角形的三条角平分线相交于一点,
并且这一点到三边的距离相等(这个交点叫做三角形的内心).4.用尺规作角的平分线.(作法)
在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理:
在一个角的内部,到一个角的两边的距离相等的点,在这个角平分线上。
4.角平分线的性质定理是证明角相等、线段相等的新途径.角平分线的逆定理是证明点在直线上(或直线经过某一点)的根据之一.3.性质定理和逆定理的关系
点在角平分线上 点到角两边的距离相等回顾: 如图1-29, 已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF 的中点. 需添加一个什么条件, 就可使CM,AM分别为∠ACD和∠CAB的平分线呢?图1-29∵ ME⊥CD, MN⊥CA,同理可得AM是∠CAB的平分线.可以添加条件MN =ME (或MN =MF).∴ M在∠ACD的平分线上,
即CM是∠ACD的平分线.图1-29∴ PE=PF.在△EBP中,BE+PE>PB,∴ BE+PF>PB.图1-30举例三.尺规作图 角平分线的作法已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC
作法:用尺规作角的平分线.1.以O为圆心,以任意长为半径画弧交OA、OB于点E、D2.分别以点D和E为圆心,以大于DE/2长为
半径作弧,两弧在∠AOB内交于点C3.作射线OC.则射线OC就是∠AOB的平分线. 如图1-31,你能在△ABC 中找到一点P,使其到三边的距离相等吗?图1-31图1-32 定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等. (这个交点叫做三角形的内心)如图,E 是∠AOB 的平分线上一点,EC⊥OA 于点C,ED⊥OB 于点D.
求证:(1)∠ECD=∠EDC; (2)OC=OD.2. 如图,在△ABC 中,AD⊥DE,BE⊥DE,AC,BC 分别平分∠BAD,∠ABE,点C在线段DE上.
求证:AB=AD+BE.M证明 作CM⊥AB于点M. ∵ AC,BC 分别平分∠BAD,∠ABE,
∴ CD = CM,CE = CM.
在Rt△ACD和Rt△ACM中,
∵ CM = CD,AC = AC,
∴ Rt△ACD ≌Rt△ACM.
∴ AD = AM.
.
同理, BE = BM.
又 AB=AM+BM,∴AB=AD+BE
挑战自我基本应用填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)∠1=∠2
DC=DE到一个角的两边的距离相等的点,在这个角平分线上。在角平分线上的点到角的两边的距离相等 1.如图,AD,AE分别是△ABC中∠A的内角平 分线和外角平分线,它们有什么关系?2. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等. 3.已知:如图,∠C=900, ∠B=300, AD是Rt△ABC的角平分线.
求证:BD=2CD. 1、如图,在△ABC中,已知 AC=BC,∠C=900,AD是△ABC的角平线,DE⊥AB,垂足为E.(1)如果CD=4cm, 求AC的长;(2)求证:AB=AC+CD.延伸训练2: 已知:如图所示:PA,PC分别是⊿ABC外角∠MAC与∠NCA平分线,它们交于P,PD⊥BM于M,PF⊥BN于F
求证: 点P在∠MBN的平分线上E3、已知:如图,∠B= ∠C=90°,M是
BC的中点,DM平分∠ ADC
求证:AM平分∠DAB。 E4、已知:△MON中,MP平分∠OMN,OP平分∠MON,且PD⊥MN,PE⊥ON,垂足分别为点D、E
求证:点P在∠MNO的平分线上小结:1.定理:
角平分线上的点到这个角的两边距离相等.2.逆定理 :
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.3.定理:三角形的三条角平分线相交于一点,
并且这一点到三边的距离相等(这个交点叫做三角形的内心).4.用尺规作角的平分线.(作法)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
