2015春湘教版数学八下1.2《直角三角形的性质和判定(II)》课件2(共16张PPT)
文档属性
| 名称 | 2015春湘教版数学八下1.2《直角三角形的性质和判定(II)》课件2(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 995.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-02 08:47:14 | ||
图片预览






文档简介
课件16张PPT。直角三角形性质和判定(2) 第一章:直角三角形1.11、直角三角形的两条性质。
2、直角三角形的两条判定。
操作探究1、在直角三角形中,如果有一个锐角
等于300,那么它所对的直角边等于斜
边的一半。阅读教材:P4—5
2、在直角三角形中,如果一条直角边等于
斜边的一半有,那么这条直角边所对的锐
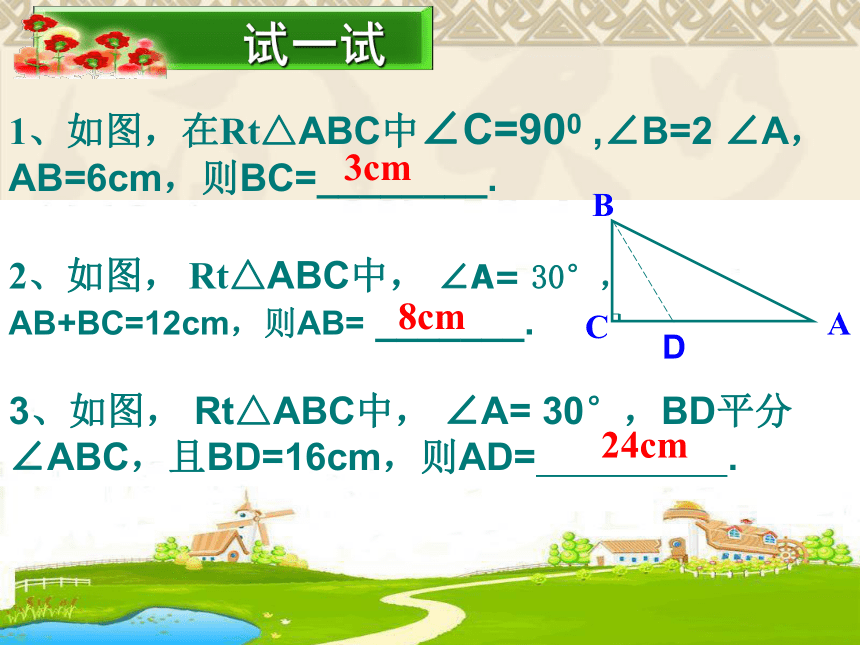
角等于30°。已知:如图,在Rt△ABC中,∠C=90°, ∠BAC=30°证明:延长BC至D,使CD=BC,连结AD.BCD∴ △ABC≌△ADC(SAS)在△ABC与△ADC中∴AB=AD又∵ △ABC 是等边三角形 判 断1)直角三角形中30°角所对的直角边等于另一直角边的一半. 2)三角形中30°角所对的边等于最长边的一半。 3)直角三角形中最小的直角边是斜边的一半。 4)直角三角形的斜边是30°角所对直角边的2倍.√ 试一试1、如图,在Rt△ABC中∠C=900 ,∠B=2 ∠A,
AB=6cm,则BC=________.2、如图, Rt△ABC中, ∠A= 30°,
AB+BC=12cm,则AB= _______.3cm8cm3、如图, Rt△ABC中, ∠A= 30°,BD平分
∠ABC,且BD=16cm,则AD= .24cmD例1.已知:如图,在△ABC中, ∠ACB= 900 ∠A=300,CD⊥AB于D.
求证:BD= AB. ACBD 课堂检测300141.在△ABC中,∠C=900, ∠B=600,BC=7,
则∠A = ----------,AB=----------2.在△ABC中,∠A: ∠B: ∠C=1:2:3,
若AB=10,则BC=----------53、如图Rt△ABC中,CD是斜边AB
上的高,若∠A=300,BD=1cm,
那么∠BCD=_____, BC=_____.3002cmABCD 课堂检测4cm2cm4、如图所示,已知△ABC中,∠ACB=900,
CD⊥AB于D, ∠A=300,且AB=8cm,
则BC= ---------- , ∠BCD=----------,
BD= ---------- ,AD= ---------- , 5、如图△ABC是等边三角形,
AB=5cm,AD⊥BC,DE⊥AB,DF⊥AC,
垂足分别为D、E、F点,
则∠ADF =______, BD=______,
BE=_______.1.25cm2.5cm60°FABCD3006cm完成教材P6练习。3、如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长.教材P7A3,56、已知:如图,在△ABC中,∠A=30°,∠ACB=90°,M、D分别为AB、MB的中点. 求证:CD⊥AB.7、如图,在Rt△ABC中,CD是斜边上的中线,CE⊥AB,已知AB=10cm,DE=2.5,求CD和∠DCE. 8、在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC= AC,求∠B 的度数及AE的长。
9、如图所示,某船于上午11时30分在A处观察海岛B位于北偏东60°,该船以每小时10海里的速度向东航行至C处,再观察海岛位于北偏东30°,且船距离海岛20海里。(1)求该船到达C处的时刻;(2)若该船从C处继续向东航行,何时到达B岛正南的D处?
2、直角三角形的两条判定。
操作探究1、在直角三角形中,如果有一个锐角
等于300,那么它所对的直角边等于斜
边的一半。阅读教材:P4—5
2、在直角三角形中,如果一条直角边等于
斜边的一半有,那么这条直角边所对的锐
角等于30°。已知:如图,在Rt△ABC中,∠C=90°, ∠BAC=30°证明:延长BC至D,使CD=BC,连结AD.BCD∴ △ABC≌△ADC(SAS)在△ABC与△ADC中∴AB=AD又∵ △ABC 是等边三角形 判 断1)直角三角形中30°角所对的直角边等于另一直角边的一半. 2)三角形中30°角所对的边等于最长边的一半。 3)直角三角形中最小的直角边是斜边的一半。 4)直角三角形的斜边是30°角所对直角边的2倍.√ 试一试1、如图,在Rt△ABC中∠C=900 ,∠B=2 ∠A,
AB=6cm,则BC=________.2、如图, Rt△ABC中, ∠A= 30°,
AB+BC=12cm,则AB= _______.3cm8cm3、如图, Rt△ABC中, ∠A= 30°,BD平分
∠ABC,且BD=16cm,则AD= .24cmD例1.已知:如图,在△ABC中, ∠ACB= 900 ∠A=300,CD⊥AB于D.
求证:BD= AB. ACBD 课堂检测300141.在△ABC中,∠C=900, ∠B=600,BC=7,
则∠A = ----------,AB=----------2.在△ABC中,∠A: ∠B: ∠C=1:2:3,
若AB=10,则BC=----------53、如图Rt△ABC中,CD是斜边AB
上的高,若∠A=300,BD=1cm,
那么∠BCD=_____, BC=_____.3002cmABCD 课堂检测4cm2cm4、如图所示,已知△ABC中,∠ACB=900,
CD⊥AB于D, ∠A=300,且AB=8cm,
则BC= ---------- , ∠BCD=----------,
BD= ---------- ,AD= ---------- , 5、如图△ABC是等边三角形,
AB=5cm,AD⊥BC,DE⊥AB,DF⊥AC,
垂足分别为D、E、F点,
则∠ADF =______, BD=______,
BE=_______.1.25cm2.5cm60°FABCD3006cm完成教材P6练习。3、如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长.教材P7A3,56、已知:如图,在△ABC中,∠A=30°,∠ACB=90°,M、D分别为AB、MB的中点. 求证:CD⊥AB.7、如图,在Rt△ABC中,CD是斜边上的中线,CE⊥AB,已知AB=10cm,DE=2.5,求CD和∠DCE. 8、在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC= AC,求∠B 的度数及AE的长。
9、如图所示,某船于上午11时30分在A处观察海岛B位于北偏东60°,该船以每小时10海里的速度向东航行至C处,再观察海岛位于北偏东30°,且船距离海岛20海里。(1)求该船到达C处的时刻;(2)若该船从C处继续向东航行,何时到达B岛正南的D处?
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
