圆的切线第一课时(湖北省襄樊市)
图片预览




文档简介
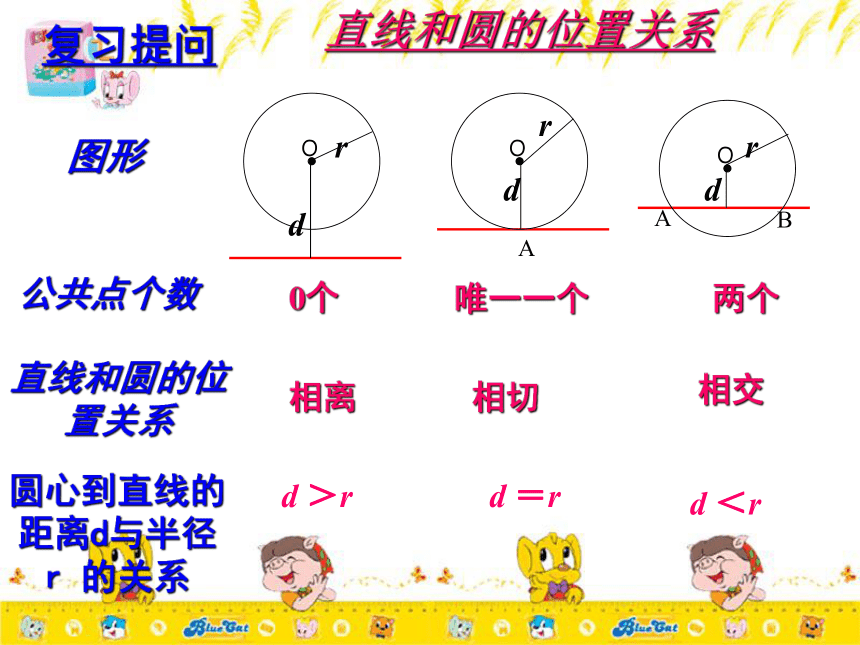
课件22张PPT。华师大版初三数学2.3圆的切线直线和圆的位置关系图形公共点个数直线和圆的位置关系圆心到直线的
距离d与半径
r 的关系
0个唯一一个两个相离相切相交d <rd =rd >r
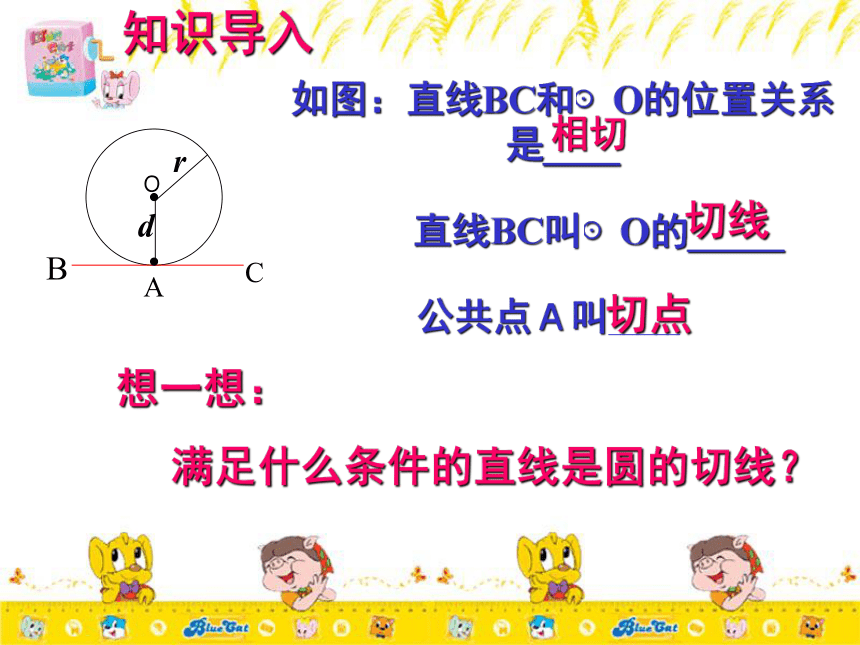
AAB复习提问知识导入如图:直线BC和⊙O的位置关系是____切线切点公共点A叫______想一想:
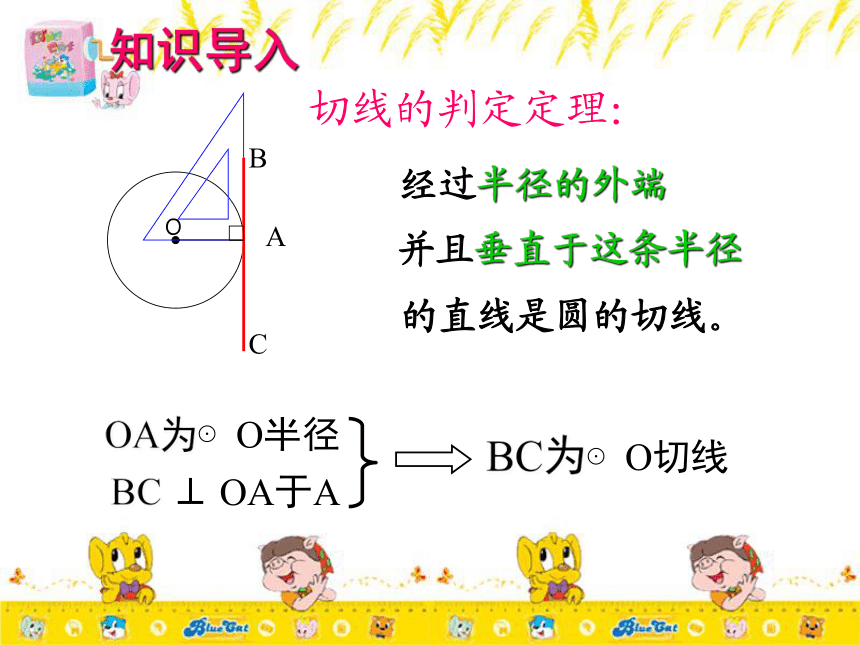
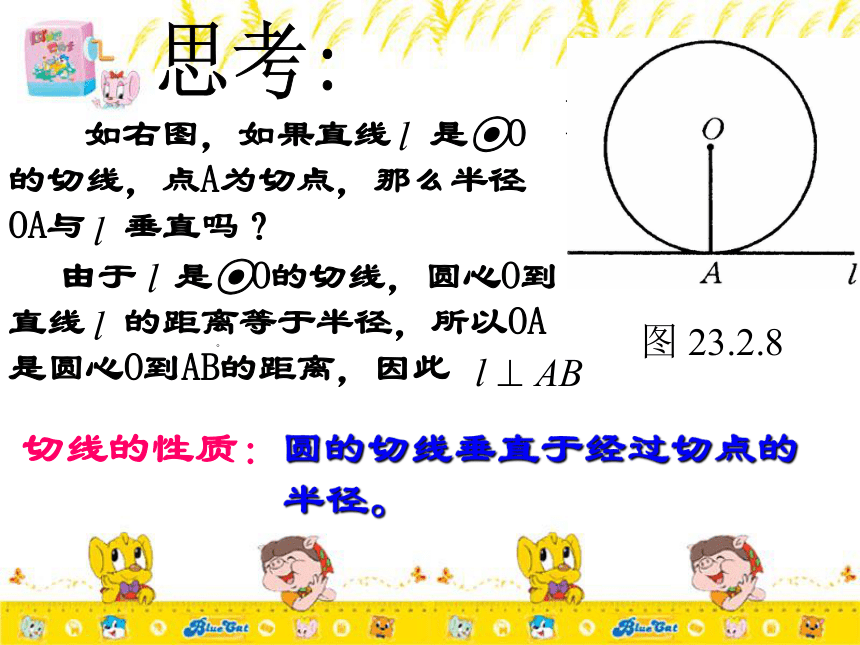
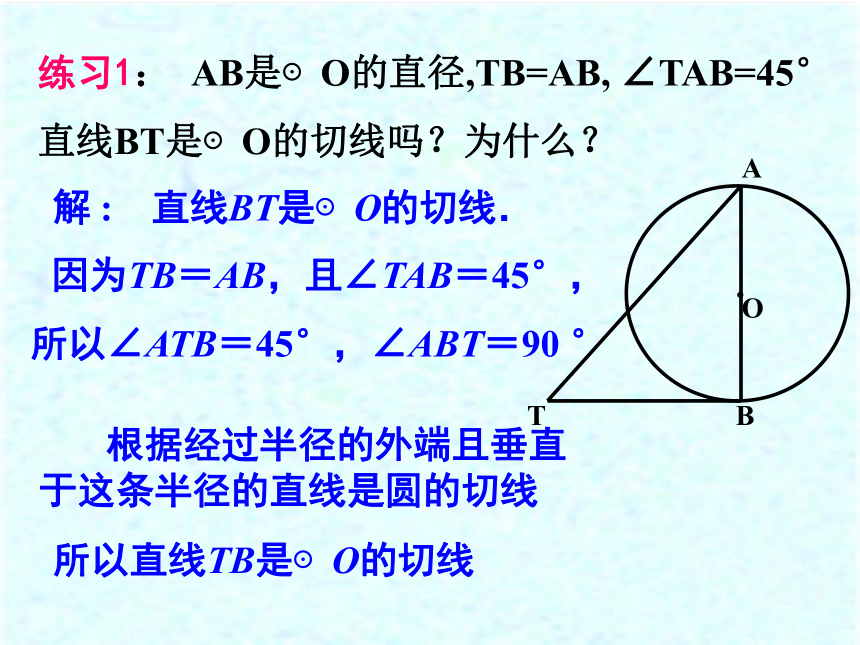
满足什么条件的直线是圆的切线?直线BC叫⊙O的_____相切知识导入BC经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定定理:OA为⊙O半径BC ⊥ OA于ABC为⊙O切线思考:温馨提示 :在此定理中,题设是“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线,1、直线l垂直于半径OA,直线l是⊙O的切线吗? 2、直线l经过半径OA的外端A,直线l是⊙O的切线吗? 不是不是切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线判定一条直线是圆的切线的三种方法1、利用定义:与圆有唯一公共点的直线是圆的切线。2、利用定理:与圆心距离等于圆的半径的直线是圆的切线。3、利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。思考:。切线的性质:圆的切线垂直于经过切点的半径。例1、如图,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么? 分析:要证明一条直线是圆的切线,必须符合两个条件,其一是这条直线是否经过半径外端,其二是这条直线是否与这条半径垂直,若满足这两个条件,就能说明这条直线是圆的切线。解 : 直线AB是⊙O的切线.因为AB=OA,且∠OBA=45°,所以∠AOB=45°,∠OAB=90 根据经过半径的外端且垂直于这条半径的直线是圆的切线 所以直线AB是⊙O的切线 练习1: AB是⊙O的直径,TB=AB, ∠TAB=45°
直线BT是⊙O的切线吗?为什么?解 : 直线BT是⊙O的切线.因为TB=AB,且∠TAB=45°,所以∠ATB=45°,∠ABT=90 ° 根据经过半径的外端且垂直于这条半径的直线是圆的切线 所以直线TB是⊙O的切线 练习2、如图已知直线AB过⊙O上的点C,并且OA=OB,CA=CB 求证:直线AB是⊙O的切线证明:连结OC∵ OA=OB,CA=CB∴ OC是等腰三角形OAB底边AB上的中线∴ AB⊥OC 因为直线AB经过半径OC的外端C,并且垂直于半径OC,所以AB是⊙O的切线证明:作OE⊥BC于E∵ 点O为∠ABC平分线上一点
OD⊥AB于D∴ OE=OD又∵ OD为⊙O半径圆心O到直线BC的距离等于半径,所以BC与⊙O相切例2、如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC是⊙O 的切线。作OE⊥BC于E 当已知条件中没有明确直线与圆是否有公共点时 辅助线:是过圆心作这条 直线的垂线段。 再证明这条垂线段的长等于半径。连结OC 当已知条件中直线与圆已有一个公共点时 辅助线:是连结圆心和这 个公共点。再证明这条半径与直线垂直。练习2、如图已知直线AB过⊙O上的点C,并且OA=OB,CA=CB
求证:直线AB是⊙O的切线例2、如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC与作⊙O相切。证明:作OE⊥AB于E∴所以AB是⊙O的切线则AE=BE连结OA又∵ 小⊙O半径为4厘米圆心O到直线AB的距离等于半径2、填空:如图AB是⊙O的直径∠ABT=45° AT=AB则AT与⊙O的位置关系是________。 1、选择:下列直线能判定为圆的切线是( )
A、与圆有公共点的直线
B、垂直于圆的半径的直线
C、过圆的半径外端的直线
D、到圆心的距离等于该圆半径的直线练习D相切
(2)、如图:在梯形ABCD中, AB∥DC,∠A=90° , 并且BC=CD+AB, 以BC为直径作⊙O 求证:AD是⊙O的切线思考题:
如图:在梯形ABCD中, AB∥DC,∠A=90° , 并且BC=CD+AB, 练习 以AB为直径作⊙O 求证:BC是⊙O的切线∴ 2OE = AD+BC=CD 练习4:已知:如图,ABCD为直角梯形,AB⊥BC,CD=AD+BC,求证:以CD为直径的圆与AB相切 过O作OE⊥AB于E。 ∴AB为⊙O的切线 即以CD为直径的圆与AB相切。∴ OE= OD∵ABCD为直角梯形,DA∥CB,CB⊥AB,DA⊥AB∴DA∥OE∥CB∵O为DC的中点证明:?练习5、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D.,BD是⊙O的切线吗?为什么?解:连结OD所以 BD是⊙O的切线BD是⊙O的切线因为AC是⊙O的直径练习6.判断:
(1)经过半径的一个端点,并且垂直于这条半径的直线是圆的切线
(2)若一条直线与圆的半径垂直,则这条直线是圆的切线。
(3)过圆的半径的外端的直线一定是这个圆的切线
(4)以直角边为半径的圆一定与另一条直角边相切。
(5)以等腰直角三角形斜边的中点为圆心,直角边的一半为半径的圆,与两条直角边相切。
(6)和圆有一个公共点的直线是圆的切线( )( )( )( )????( )?( )? 练习7.下列命题中的假命题是:
A.和圆有唯一公共点的直线是圆的切线 B.过直径一端且垂直于这条直径的直线是圆的切线 C.点A在直线L上,⊙O半径为r,若OA=r时,则
直线L是⊙O的切线 D.⊙O的半径为a,则O点到直线的距离为d,若d=
a时,则L是⊙O的切线。( )C切线的性质:圆的切线垂直于经过切点的半径。判定一条直线是圆的切线的三种方法1、利用定义:与圆有唯一公共点的直线是圆的切线。2、利用定理:与圆心距离等与圆的半径的直线是圆的切线。3、利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。小结小结要判定一条直线是圆的切线,我们已学过三种方法,如下表所示:有切点,连半径,证垂直无切点,作垂直,证半径今天,你有哪些收获?作 业课本P63习题7、12
距离d与半径
r 的关系
0个唯一一个两个相离相切相交d <rd =rd >r
AAB复习提问知识导入如图:直线BC和⊙O的位置关系是____切线切点公共点A叫______想一想:
满足什么条件的直线是圆的切线?直线BC叫⊙O的_____相切知识导入BC经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定定理:OA为⊙O半径BC ⊥ OA于ABC为⊙O切线思考:温馨提示 :在此定理中,题设是“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线,1、直线l垂直于半径OA,直线l是⊙O的切线吗? 2、直线l经过半径OA的外端A,直线l是⊙O的切线吗? 不是不是切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线判定一条直线是圆的切线的三种方法1、利用定义:与圆有唯一公共点的直线是圆的切线。2、利用定理:与圆心距离等于圆的半径的直线是圆的切线。3、利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。思考:。切线的性质:圆的切线垂直于经过切点的半径。例1、如图,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么? 分析:要证明一条直线是圆的切线,必须符合两个条件,其一是这条直线是否经过半径外端,其二是这条直线是否与这条半径垂直,若满足这两个条件,就能说明这条直线是圆的切线。解 : 直线AB是⊙O的切线.因为AB=OA,且∠OBA=45°,所以∠AOB=45°,∠OAB=90 根据经过半径的外端且垂直于这条半径的直线是圆的切线 所以直线AB是⊙O的切线 练习1: AB是⊙O的直径,TB=AB, ∠TAB=45°
直线BT是⊙O的切线吗?为什么?解 : 直线BT是⊙O的切线.因为TB=AB,且∠TAB=45°,所以∠ATB=45°,∠ABT=90 ° 根据经过半径的外端且垂直于这条半径的直线是圆的切线 所以直线TB是⊙O的切线 练习2、如图已知直线AB过⊙O上的点C,并且OA=OB,CA=CB 求证:直线AB是⊙O的切线证明:连结OC∵ OA=OB,CA=CB∴ OC是等腰三角形OAB底边AB上的中线∴ AB⊥OC 因为直线AB经过半径OC的外端C,并且垂直于半径OC,所以AB是⊙O的切线证明:作OE⊥BC于E∵ 点O为∠ABC平分线上一点
OD⊥AB于D∴ OE=OD又∵ OD为⊙O半径圆心O到直线BC的距离等于半径,所以BC与⊙O相切例2、如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC是⊙O 的切线。作OE⊥BC于E 当已知条件中没有明确直线与圆是否有公共点时 辅助线:是过圆心作这条 直线的垂线段。 再证明这条垂线段的长等于半径。连结OC 当已知条件中直线与圆已有一个公共点时 辅助线:是连结圆心和这 个公共点。再证明这条半径与直线垂直。练习2、如图已知直线AB过⊙O上的点C,并且OA=OB,CA=CB
求证:直线AB是⊙O的切线例2、如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC与作⊙O相切。证明:作OE⊥AB于E∴所以AB是⊙O的切线则AE=BE连结OA又∵ 小⊙O半径为4厘米圆心O到直线AB的距离等于半径2、填空:如图AB是⊙O的直径∠ABT=45° AT=AB则AT与⊙O的位置关系是________。 1、选择:下列直线能判定为圆的切线是( )
A、与圆有公共点的直线
B、垂直于圆的半径的直线
C、过圆的半径外端的直线
D、到圆心的距离等于该圆半径的直线练习D相切
(2)、如图:在梯形ABCD中, AB∥DC,∠A=90° , 并且BC=CD+AB, 以BC为直径作⊙O 求证:AD是⊙O的切线思考题:
如图:在梯形ABCD中, AB∥DC,∠A=90° , 并且BC=CD+AB, 练习 以AB为直径作⊙O 求证:BC是⊙O的切线∴ 2OE = AD+BC=CD 练习4:已知:如图,ABCD为直角梯形,AB⊥BC,CD=AD+BC,求证:以CD为直径的圆与AB相切 过O作OE⊥AB于E。 ∴AB为⊙O的切线 即以CD为直径的圆与AB相切。∴ OE= OD∵ABCD为直角梯形,DA∥CB,CB⊥AB,DA⊥AB∴DA∥OE∥CB∵O为DC的中点证明:?练习5、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D.,BD是⊙O的切线吗?为什么?解:连结OD所以 BD是⊙O的切线BD是⊙O的切线因为AC是⊙O的直径练习6.判断:
(1)经过半径的一个端点,并且垂直于这条半径的直线是圆的切线
(2)若一条直线与圆的半径垂直,则这条直线是圆的切线。
(3)过圆的半径的外端的直线一定是这个圆的切线
(4)以直角边为半径的圆一定与另一条直角边相切。
(5)以等腰直角三角形斜边的中点为圆心,直角边的一半为半径的圆,与两条直角边相切。
(6)和圆有一个公共点的直线是圆的切线( )( )( )( )????( )?( )? 练习7.下列命题中的假命题是:
A.和圆有唯一公共点的直线是圆的切线 B.过直径一端且垂直于这条直径的直线是圆的切线 C.点A在直线L上,⊙O半径为r,若OA=r时,则
直线L是⊙O的切线 D.⊙O的半径为a,则O点到直线的距离为d,若d=
a时,则L是⊙O的切线。( )C切线的性质:圆的切线垂直于经过切点的半径。判定一条直线是圆的切线的三种方法1、利用定义:与圆有唯一公共点的直线是圆的切线。2、利用定理:与圆心距离等与圆的半径的直线是圆的切线。3、利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。小结小结要判定一条直线是圆的切线,我们已学过三种方法,如下表所示:有切点,连半径,证垂直无切点,作垂直,证半径今天,你有哪些收获?作 业课本P63习题7、12
