人教版八年级数学(上)同步评估卷(五)第十四章 轴对称(14.1、14.2)(浙江省台州市路桥区)
文档属性
| 名称 | 人教版八年级数学(上)同步评估卷(五)第十四章 轴对称(14.1、14.2)(浙江省台州市路桥区) |

|
|
| 格式 | rar | ||
| 文件大小 | 495.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-12 00:00:00 | ||
图片预览

文档简介
人教版八年级数学(上)同步评估卷(五)
第十二章 轴对称(12.1、12.2)
班级_______ 姓名________号次_________
一.选择题(每小题3分,共30分)
1.下列图形中,是轴对称图形的为( )
2.在平面直角坐标系中,ΔABC与ΔAˊBˊCˊ关于直线l成轴对称,则两个三角形的面积的关系是( )
A. 变大 B. 变小 C. 不变 D. 不确定
3. 点P(-2,5)关于y轴对称的点Pˊ的坐标是( )
A.(2,-5) B.(-2,-5) C.(2,5) D.(5,-2)
4.下列说法正确的是( )
A.任何一个图形都有对称轴; B.两个全等三角形一定关于某直线对称;
C.若△ABC与△A′B′C′成轴对称,则△ABC≌△A′B′C′;
D.点A、点B在直线1两旁,且AB与直线1交于点O,若AO=BO,则点A与点B关于直线l对称.
5. 将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到的是( )
A. B. C. D.
6. 在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应是( )
A. 21:02 B. 21:05
C. 20:15 D. 20:05
7. 如图,有A、B、C三个村庄,现要建一个车站,到三个村庄的距
离相等,这样的车站选址有( )
A. 1处 B. 2处 C. 3处 D. 4处
8.已知A、B两点的坐标分别是(-1,2)和(1,2),则下面四个结论:①A、B两点关于x轴对称;②A、B两点关于y轴对称;③A、B两点关于原点对称;④A、B两点之间的距离为2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图 ,∠C=90°,AB的垂直平分线交BC于D,连接AD,
若∠CAD=20°,则∠B=( )
A.20° B.30° C.35° D.40°
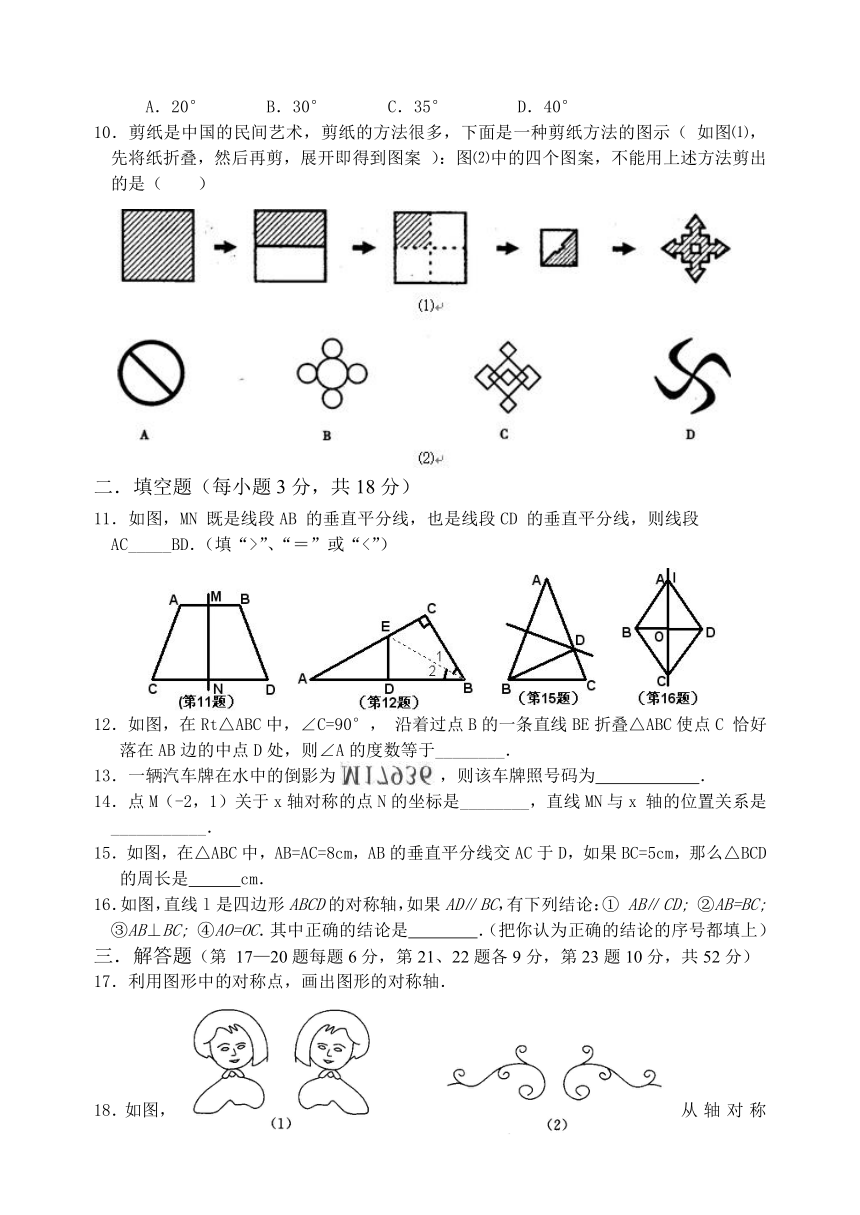
10.剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(如图⑴,先将纸折叠,然后再剪,展开即得到图案 ):图⑵中的四个图案,不能用上述方法剪出的是( )
二.填空题(每小题3分,共18分)
11.如图,MN既是线段AB的垂直平分线,也是线段CD的垂直平分线,则线段AC_____BD.(填“>”、“=”或“<”)
12.如图,在Rt△ABC中,∠C=90°, 沿着过点B的一条直线BE折叠△ABC使点C恰好落在AB边的中点D处,则∠A的度数等于________.
13.一辆汽车牌在水中的倒影为 ,则该车牌照号码为 .
14.点M(-2,1)关于x轴对称的点N的坐标是________,直线MN与x轴的位置关系是___________.
15.如图,在△ABC中,AB=AC=8cm,AB的垂直平分线交AC于D,如果BC=5cm,那么△BCD的周长是 cm.
16.如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:① AB∥CD; ②AB=BC; ③AB⊥BC; ④AO=OC.其中正确的结论是 .(把你认为正确的结论的序号都填上)
三.解答题(第 17 —20题每题6分,第21、22题各9分,第23题10分,共52分)
17.利用图形中的对称点,画出图形的对称轴.
18.如图,从轴对称的角度来看,你觉得哪一个图形比较独特?简单说明你的道理.
19.小明家中客厅的南北长度是6m,在客厅西墙上装了一面很大很大的镜子,客厅的门在东墙.某日小敏去小明家,刚进门就说:“呀,你家客厅好大呀,估计有50多平方米吧?”小说:“没有,不足30平方米.”请你解释,两人的估算怎么会差别如此之大?究竟谁说错了呢?
20.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹).
21.如图:①写出A、B、C三点的坐标.
②若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A′、B′、C′,并依次连接这三个点,所得的△A′B′C′与原△ABC有怎样的位置关系?
③在②的基础上,纵坐标都不变,横坐标都乘以-1,在同一坐标系中描出对应的点
A″、B″、C″,并依次连接这三个点,所得的△A″B″C″与原△ABC有怎样的位置关系?
22.如图,AB=AC,DB=DC,E是AD延长线上的一点,BE是否与CE相等?试说明理由.
23.如图,已知AB比AC长3cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是15cm,求AB和AC的长.
四.选做题(10分)
24. 如图,在ΔABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;
(2)若∠ACB为a,则∠ECD的度数能否用含a的式子来表示.
轴对称(12.1、12.2)答案:
一.选择题 1.B 2.C 3. C 4. C 5. C 6. B 7. A 8. B 9. C 10. D
二.填空题 11. = 12. 30° 13. M17936 14.(-2,-1), 互相垂直 15. 13cm
16. ①②④
三.解答题(第17---20题每题6分,第21、22各9 分,第23题10分,共52分)
17. 图略
18.丁比较独特,丁图形有无数条对称轴,而其他图形只有两条对称轴.
19.都对,小敏把镜子里看到的都算在一起了,小明说的是实际面积.
20.图略
21.① A(3,4) B(1,2) C(5,1)
②图略, 关于x轴对称
③图略, 关于原点对称
22.答:相等 理由:连接BC,∵AB=AC, ∴点A在线段BC的垂直平分线上.
同理,点D也在线段BC的垂直平分线上,
∵两点确定一条直线, ∴AD是线段BC的垂直平分线.
∵E是AD延长线上的一点, ∴BE=EC.
23.解:∵DE垂直平分BC, ∴DB=DC.
∵AC+AD+DC=15cm, ∴AC+AD+BD=15cm, 即AC+AB=15cm.
又∵AB-AC=3cm, 解 得AB=9,AC=6
答:AB长为9cm,AC长为6cm.
24.(1) ∵AF垂直平分CD,BG垂直平分CE, ∴AC=AD,BC=BE,
∴∠ADC=∠ACD, ∠BCE=∠BEC. ∵∠ACB=90°,∴∠BAC+∠ABC=90°,
∴∠ADC+∠ACD+∠BEC+∠BCE=270°.
∴2∠ADC+2∠BEC=270°, ∴∠ADC+∠BEC=135°. ∴ ∠ECD=180°-135°=45°
(2) ∵∠ADC=∠ACD, ∠BEC=∠BCE,又∵∠BAC+∠ADC+∠ACD+∠BEC+∠ABC=360°, ∴ ∠BAC+2∠ADC+2∠BEC+∠ABC=360°.
∵∠ACB=,∴ ∠BAC+∠ABC=180°-,∴2∠ADC+2∠BEC+180°-=360°. ∴2∠ADC+2∠BEC=180°+, ∠ADC+∠BEC=90°+,
∵∠EDC+∠DEC+∠ECD=180°,
∴∠EDC=180°-(∠ECD+∠DEC)=180°-90°-=90°- .
∶
第十二章 轴对称(12.1、12.2)
班级_______ 姓名________号次_________
一.选择题(每小题3分,共30分)
1.下列图形中,是轴对称图形的为( )
2.在平面直角坐标系中,ΔABC与ΔAˊBˊCˊ关于直线l成轴对称,则两个三角形的面积的关系是( )
A. 变大 B. 变小 C. 不变 D. 不确定
3. 点P(-2,5)关于y轴对称的点Pˊ的坐标是( )
A.(2,-5) B.(-2,-5) C.(2,5) D.(5,-2)
4.下列说法正确的是( )
A.任何一个图形都有对称轴; B.两个全等三角形一定关于某直线对称;
C.若△ABC与△A′B′C′成轴对称,则△ABC≌△A′B′C′;
D.点A、点B在直线1两旁,且AB与直线1交于点O,若AO=BO,则点A与点B关于直线l对称.
5. 将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到的是( )
A. B. C. D.
6. 在平面镜里看到背后墙上的电子钟示数如图所示,这时的实际时间应是( )
A. 21:02 B. 21:05
C. 20:15 D. 20:05
7. 如图,有A、B、C三个村庄,现要建一个车站,到三个村庄的距
离相等,这样的车站选址有( )
A. 1处 B. 2处 C. 3处 D. 4处
8.已知A、B两点的坐标分别是(-1,2)和(1,2),则下面四个结论:①A、B两点关于x轴对称;②A、B两点关于y轴对称;③A、B两点关于原点对称;④A、B两点之间的距离为2,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图 ,∠C=90°,AB的垂直平分线交BC于D,连接AD,
若∠CAD=20°,则∠B=( )
A.20° B.30° C.35° D.40°
10.剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(如图⑴,先将纸折叠,然后再剪,展开即得到图案 ):图⑵中的四个图案,不能用上述方法剪出的是( )
二.填空题(每小题3分,共18分)
11.如图,MN既是线段AB的垂直平分线,也是线段CD的垂直平分线,则线段AC_____BD.(填“>”、“=”或“<”)
12.如图,在Rt△ABC中,∠C=90°, 沿着过点B的一条直线BE折叠△ABC使点C恰好落在AB边的中点D处,则∠A的度数等于________.
13.一辆汽车牌在水中的倒影为 ,则该车牌照号码为 .
14.点M(-2,1)关于x轴对称的点N的坐标是________,直线MN与x轴的位置关系是___________.
15.如图,在△ABC中,AB=AC=8cm,AB的垂直平分线交AC于D,如果BC=5cm,那么△BCD的周长是 cm.
16.如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:① AB∥CD; ②AB=BC; ③AB⊥BC; ④AO=OC.其中正确的结论是 .(把你认为正确的结论的序号都填上)
三.解答题(第 17 —20题每题6分,第21、22题各9分,第23题10分,共52分)
17.利用图形中的对称点,画出图形的对称轴.
18.如图,从轴对称的角度来看,你觉得哪一个图形比较独特?简单说明你的道理.
19.小明家中客厅的南北长度是6m,在客厅西墙上装了一面很大很大的镜子,客厅的门在东墙.某日小敏去小明家,刚进门就说:“呀,你家客厅好大呀,估计有50多平方米吧?”小说:“没有,不足30平方米.”请你解释,两人的估算怎么会差别如此之大?究竟谁说错了呢?
20.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹).
21.如图:①写出A、B、C三点的坐标.
②若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A′、B′、C′,并依次连接这三个点,所得的△A′B′C′与原△ABC有怎样的位置关系?
③在②的基础上,纵坐标都不变,横坐标都乘以-1,在同一坐标系中描出对应的点
A″、B″、C″,并依次连接这三个点,所得的△A″B″C″与原△ABC有怎样的位置关系?
22.如图,AB=AC,DB=DC,E是AD延长线上的一点,BE是否与CE相等?试说明理由.
23.如图,已知AB比AC长3cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是15cm,求AB和AC的长.
四.选做题(10分)
24. 如图,在ΔABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;
(2)若∠ACB为a,则∠ECD的度数能否用含a的式子来表示.
轴对称(12.1、12.2)答案:
一.选择题 1.B 2.C 3. C 4. C 5. C 6. B 7. A 8. B 9. C 10. D
二.填空题 11. = 12. 30° 13. M17936 14.(-2,-1), 互相垂直 15. 13cm
16. ①②④
三.解答题(第17---20题每题6分,第21、22各9 分,第23题10分,共52分)
17. 图略
18.丁比较独特,丁图形有无数条对称轴,而其他图形只有两条对称轴.
19.都对,小敏把镜子里看到的都算在一起了,小明说的是实际面积.
20.图略
21.① A(3,4) B(1,2) C(5,1)
②图略, 关于x轴对称
③图略, 关于原点对称
22.答:相等 理由:连接BC,∵AB=AC, ∴点A在线段BC的垂直平分线上.
同理,点D也在线段BC的垂直平分线上,
∵两点确定一条直线, ∴AD是线段BC的垂直平分线.
∵E是AD延长线上的一点, ∴BE=EC.
23.解:∵DE垂直平分BC, ∴DB=DC.
∵AC+AD+DC=15cm, ∴AC+AD+BD=15cm, 即AC+AB=15cm.
又∵AB-AC=3cm, 解 得AB=9,AC=6
答:AB长为9cm,AC长为6cm.
24.(1) ∵AF垂直平分CD,BG垂直平分CE, ∴AC=AD,BC=BE,
∴∠ADC=∠ACD, ∠BCE=∠BEC. ∵∠ACB=90°,∴∠BAC+∠ABC=90°,
∴∠ADC+∠ACD+∠BEC+∠BCE=270°.
∴2∠ADC+2∠BEC=270°, ∴∠ADC+∠BEC=135°. ∴ ∠ECD=180°-135°=45°
(2) ∵∠ADC=∠ACD, ∠BEC=∠BCE,又∵∠BAC+∠ADC+∠ACD+∠BEC+∠ABC=360°, ∴ ∠BAC+2∠ADC+2∠BEC+∠ABC=360°.
∵∠ACB=,∴ ∠BAC+∠ABC=180°-,∴2∠ADC+2∠BEC+180°-=360°. ∴2∠ADC+2∠BEC=180°+, ∠ADC+∠BEC=90°+,
∵∠EDC+∠DEC+∠ECD=180°,
∴∠EDC=180°-(∠ECD+∠DEC)=180°-90°-=90°- .
∶
