人教版八年级数学(上)同步评估卷(六) 第十四章 等腰三角形(浙江省台州市路桥区)
文档属性
| 名称 | 人教版八年级数学(上)同步评估卷(六) 第十四章 等腰三角形(浙江省台州市路桥区) |  | |
| 格式 | rar | ||
| 文件大小 | 405.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-12 16:28:00 | ||
图片预览

文档简介
人教版八年级数学(上)同步评估卷(六)
第十二章 等腰三角形(12.3)
班级_______ 姓名________号次_________
一.选择题(每小题3分,共30分)
1.下列说法中,正确的有 ( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个 B.2个 C.3个 D.4个
2.等腰三角形有两条边长为4cm和6cm,则该三角形的周长是( )
A.14cm B.16cm C.14cm或16cm D.12cm
3.等腰三角形的一个外角是80°,则其底角是( )
A.100° B.100°或40° C.40° D.80°
4.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③ B.①②④ C.①③ D.①②③④
5.同学们都玩过跷跷板的游戏.如图所示,是一跷跷板的示意图,立柱OC与地面垂直,OA=OB.当跷跷板的一头A着地时,∠OAC=25°,则当跷跷板的另一头B着地时,
∠AOA′等于( )
A.25° B.50° C.60° D.130°
(第5题) (第7题) (第8题)
6.等边三角形△ABC的两条角平分线BD和CE交于点I,则∠BIC等于( )
A.60° B.90° C.120° D.150°
7.如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是( )
A.∠ACD=∠B B.CH=CE=EF C.CH=HD D.AC=AF
8.如图,在△ABC中,∠C=90°,DE垂直平分AB于E,交AC于D,AD=2BC,则∠A等于( )
A.15° B.25° C. 30° D. 35°
9.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.(1)(2)(3) B.(1)(2)(4) C. (2)(3)(4) D.(1)(3)(4)
A.(1)(2)(3) B.(1)(2)(4) C. (2)(3)(4) D.(1)(3)(4)
10.在平面直角坐标系xOy中,已知A(2,-2),在y轴确定点P,使△AOP为等腰三角形,则符合条件的点有 ( )
A.2个 B.3个 C.4个 D.5个
二.填空题(每小题3分,共18分)
11.△ABC中,AB=AC,∠A=∠C,则∠B=_______.
12. △ABC中,∠C=∠B, D、E分别是AB、AC上的点,AE=2cm,且DE∥BC,则AD=_______.
13.△ABC中,∠B=∠C=15°,AB=2cm,CD⊥AB交BA的延长线于点D,则CD的长度是_______.
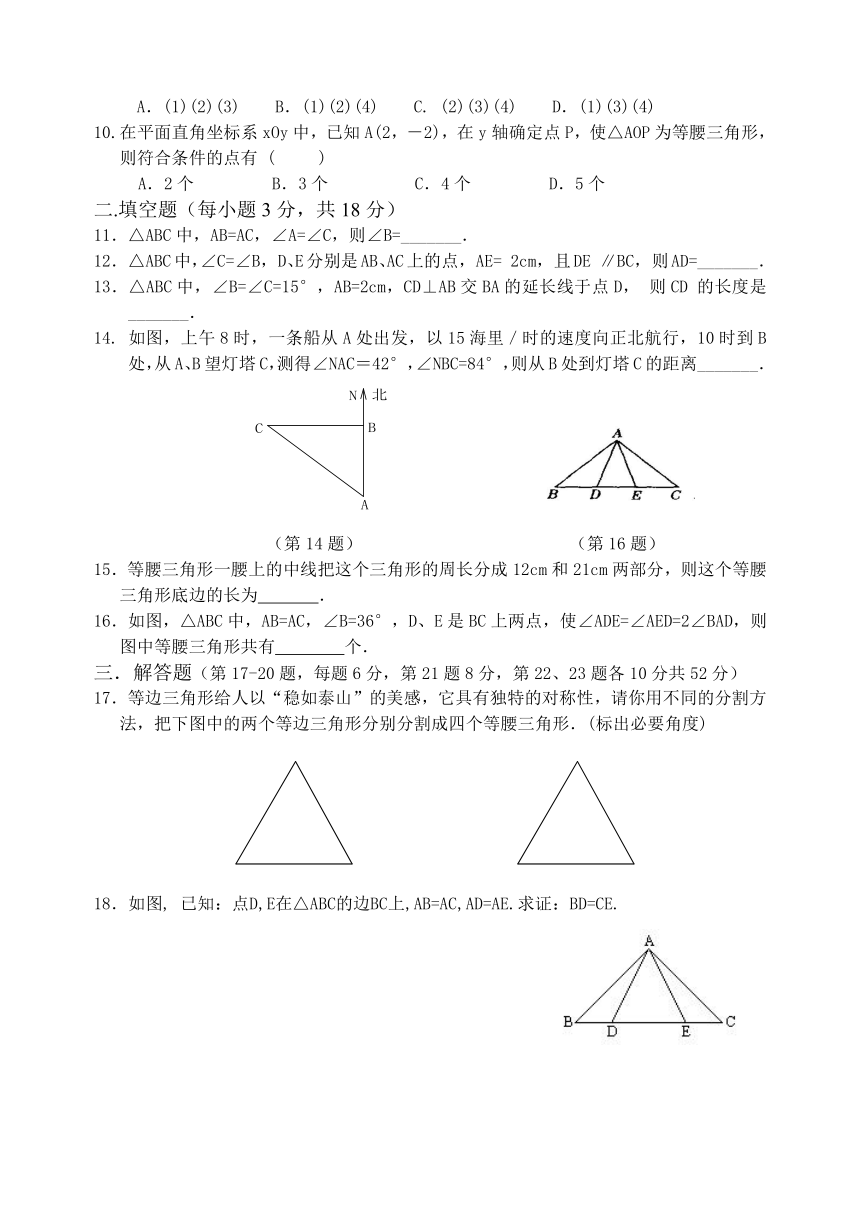
14. 如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
(第14题) (第16题)
15.等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,则这个等腰三角形底边的长为 .
16.如图,△ABC中,AB=AC,∠B=36°,D、E是BC上两点,使∠ADE=∠AED=2∠BAD,则图中等腰三角形共有 个.
三.解答题(第17-20题,每题6分,第21题8分,第22、23题各10分共52分)
17.等边三角形给人以“稳如泰山”的美感,它具有独特的对称性,请你用不同的分割方法,把下图中的两个等边三角形分别分割成四个等腰三角形.(标出必要角度)
18.如图, 已知:点D,E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE.
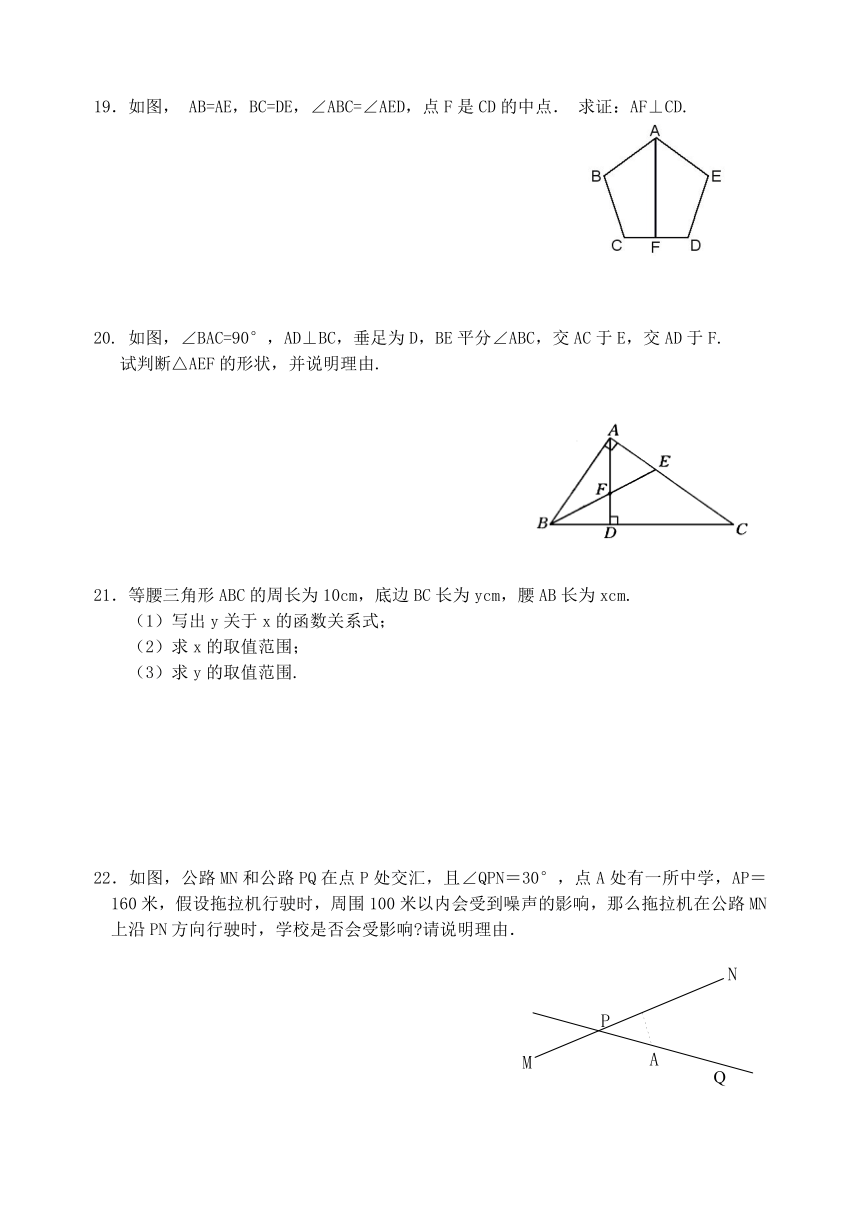
19.如图, AB=AE,BC=DE,∠ABC=∠AED,点F是CD的中点.求证:AF⊥CD.
20. 如图,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F.
试判断△AEF的形状,并说明理由.
21.等腰三角形ABC的周长为10cm,底边BC长为ycm,腰AB长为xcm.
(1)写出y关于x的函数关系式;
(2)求x的取值范围;
(3)求y的取值范围.
22.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160米,假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受影响 请说明理由.
23.如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数.(提示:连接CE)
四.选做题(10分)
24.小红和小兵一起做一道题:依据下面条件求等腰三角形的三个内角的度数.(1)一个角为另一个角的2倍;(2)两角之差为30°.
小兵做出了以下解答过程:
(1)设等腰三角形的顶角为x°,则底角为2x,由题意得x+2x+2x=180°,解得x=36,所以2x=72,所以这个等腰三角形的三个内角为36°,72°,72°.
小红做出了以下解答过程:
(2)设等腰三角形的顶角为x°,则底角为(x+30°),由题意得x+2(x+30)=180,解得x=40,所以x+30=70,所以这个等腰三角形的三个内角度数为40°,70°,70°.
小红看了解答以后说:“小兵你错了”.
亲爱的同学,你说他们的答案到底谁错了?错在哪里呢?
等腰三角形(12.3)答案:
一.选择题 1.D 2.C 3. C 4. D 5. B 6. C 7. C 8. A 9. D 10. C
二.填空题 11. 60° 12. 2cm, 13. 1cm 14. 30海里 15. 5cm 16. 6个
三.解答题(第17---20题每题6分,第21、22各9 分,第23题10分,共52分)
17.
18.证明:∵AB=AC,AD=AE ∴∠B=∠C,∠ADE=∠AED ∴∠BAD=∠CAE
在ΔABD与ΔACE中
∴△ABD≌△CAE(SAS) ∴AC=AD
19. 证明:连接AC、AD . 在△ABC和△AED中
∴△ABC≌△AED(SAS) ∴AC=AD
又∵△ACD中AF是CD边的中线 ∴AF⊥CD
20.答:是等腰三角形.
理由: ∵BE平分∠ABC, ∴∠1=∠2.
又∵∠BAC=90°,AD⊥BC,
∴∠3=90°-∠1,∠4=90°-∠2, ∴∠3=∠4.
又∵∠4=∠5,∴∠3=∠5, ∴△AEF是等腰三角形.
21.解:(1)y=10-2x.
(2)∵x,y为线段,∴x>0,y>0. ∴10-2x>0,∴O<x<5.①
又∵x,y为三角形边长, ∴x+x>y,即2x>10-2x.②
由①②可得x的取值范围是2.5<x<5.
(3)∵2.5<x<5,∴5<2x<10,∴-10<-2x<-5,∴O<10-2x<5,
∴O<y<5. ∴y的取值范围是O<y<5.
22. 答:会受到影响.
理由:过点A作AB⊥MN于点B, 在RtΔABP中,∠QPN=30°
故AB=AP=80米 < 100米, 所以学校会受到影响。
23.连接CE,先证明△BCE≌△ACE得到∠BCE=∠ACE=30°,
再证明△BDE≌△BCE得到∠BDE=∠BCE=30°.
24.解:他们的答案都不对,小兵的答案只满足条件(1),而小红的答案只满足条件(2).
应设一角为x,则有一角为2x,第三角为x或2x,当第三角为x时,解得x=30°,
2x=60°,三个内角和等于120°,不满足题意(舍去),
而当第三角为2x时,解得x=30°,2x=60°,三个内角和为150°,也不满足,
所以此题没有解.
Q
第十二章 等腰三角形(12.3)
班级_______ 姓名________号次_________
一.选择题(每小题3分,共30分)
1.下列说法中,正确的有 ( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个 B.2个 C.3个 D.4个
2.等腰三角形有两条边长为4cm和6cm,则该三角形的周长是( )
A.14cm B.16cm C.14cm或16cm D.12cm
3.等腰三角形的一个外角是80°,则其底角是( )
A.100° B.100°或40° C.40° D.80°
4.下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )
A.①②③ B.①②④ C.①③ D.①②③④
5.同学们都玩过跷跷板的游戏.如图所示,是一跷跷板的示意图,立柱OC与地面垂直,OA=OB.当跷跷板的一头A着地时,∠OAC=25°,则当跷跷板的另一头B着地时,
∠AOA′等于( )
A.25° B.50° C.60° D.130°
(第5题) (第7题) (第8题)
6.等边三角形△ABC的两条角平分线BD和CE交于点I,则∠BIC等于( )
A.60° B.90° C.120° D.150°
7.如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是( )
A.∠ACD=∠B B.CH=CE=EF C.CH=HD D.AC=AF
8.如图,在△ABC中,∠C=90°,DE垂直平分AB于E,交AC于D,AD=2BC,则∠A等于( )
A.15° B.25° C. 30° D. 35°
9.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A.(1)(2)(3) B.(1)(2)(4) C. (2)(3)(4) D.(1)(3)(4)
A.(1)(2)(3) B.(1)(2)(4) C. (2)(3)(4) D.(1)(3)(4)
10.在平面直角坐标系xOy中,已知A(2,-2),在y轴确定点P,使△AOP为等腰三角形,则符合条件的点有 ( )
A.2个 B.3个 C.4个 D.5个
二.填空题(每小题3分,共18分)
11.△ABC中,AB=AC,∠A=∠C,则∠B=_______.
12. △ABC中,∠C=∠B, D、E分别是AB、AC上的点,AE=2cm,且DE∥BC,则AD=_______.
13.△ABC中,∠B=∠C=15°,AB=2cm,CD⊥AB交BA的延长线于点D,则CD的长度是_______.
14. 如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
(第14题) (第16题)
15.等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,则这个等腰三角形底边的长为 .
16.如图,△ABC中,AB=AC,∠B=36°,D、E是BC上两点,使∠ADE=∠AED=2∠BAD,则图中等腰三角形共有 个.
三.解答题(第17-20题,每题6分,第21题8分,第22、23题各10分共52分)
17.等边三角形给人以“稳如泰山”的美感,它具有独特的对称性,请你用不同的分割方法,把下图中的两个等边三角形分别分割成四个等腰三角形.(标出必要角度)
18.如图, 已知:点D,E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE.
19.如图, AB=AE,BC=DE,∠ABC=∠AED,点F是CD的中点.求证:AF⊥CD.
20. 如图,∠BAC=90°,AD⊥BC,垂足为D,BE平分∠ABC,交AC于E,交AD于F.
试判断△AEF的形状,并说明理由.
21.等腰三角形ABC的周长为10cm,底边BC长为ycm,腰AB长为xcm.
(1)写出y关于x的函数关系式;
(2)求x的取值范围;
(3)求y的取值范围.
22.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160米,假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受影响 请说明理由.
23.如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数.(提示:连接CE)
四.选做题(10分)
24.小红和小兵一起做一道题:依据下面条件求等腰三角形的三个内角的度数.(1)一个角为另一个角的2倍;(2)两角之差为30°.
小兵做出了以下解答过程:
(1)设等腰三角形的顶角为x°,则底角为2x,由题意得x+2x+2x=180°,解得x=36,所以2x=72,所以这个等腰三角形的三个内角为36°,72°,72°.
小红做出了以下解答过程:
(2)设等腰三角形的顶角为x°,则底角为(x+30°),由题意得x+2(x+30)=180,解得x=40,所以x+30=70,所以这个等腰三角形的三个内角度数为40°,70°,70°.
小红看了解答以后说:“小兵你错了”.
亲爱的同学,你说他们的答案到底谁错了?错在哪里呢?
等腰三角形(12.3)答案:
一.选择题 1.D 2.C 3. C 4. D 5. B 6. C 7. C 8. A 9. D 10. C
二.填空题 11. 60° 12. 2cm, 13. 1cm 14. 30海里 15. 5cm 16. 6个
三.解答题(第17---20题每题6分,第21、22各9 分,第23题10分,共52分)
17.
18.证明:∵AB=AC,AD=AE ∴∠B=∠C,∠ADE=∠AED ∴∠BAD=∠CAE
在ΔABD与ΔACE中
∴△ABD≌△CAE(SAS) ∴AC=AD
19. 证明:连接AC、AD . 在△ABC和△AED中
∴△ABC≌△AED(SAS) ∴AC=AD
又∵△ACD中AF是CD边的中线 ∴AF⊥CD
20.答:是等腰三角形.
理由: ∵BE平分∠ABC, ∴∠1=∠2.
又∵∠BAC=90°,AD⊥BC,
∴∠3=90°-∠1,∠4=90°-∠2, ∴∠3=∠4.
又∵∠4=∠5,∴∠3=∠5, ∴△AEF是等腰三角形.
21.解:(1)y=10-2x.
(2)∵x,y为线段,∴x>0,y>0. ∴10-2x>0,∴O<x<5.①
又∵x,y为三角形边长, ∴x+x>y,即2x>10-2x.②
由①②可得x的取值范围是2.5<x<5.
(3)∵2.5<x<5,∴5<2x<10,∴-10<-2x<-5,∴O<10-2x<5,
∴O<y<5. ∴y的取值范围是O<y<5.
22. 答:会受到影响.
理由:过点A作AB⊥MN于点B, 在RtΔABP中,∠QPN=30°
故AB=AP=80米 < 100米, 所以学校会受到影响。
23.连接CE,先证明△BCE≌△ACE得到∠BCE=∠ACE=30°,
再证明△BDE≌△BCE得到∠BDE=∠BCE=30°.
24.解:他们的答案都不对,小兵的答案只满足条件(1),而小红的答案只满足条件(2).
应设一角为x,则有一角为2x,第三角为x或2x,当第三角为x时,解得x=30°,
2x=60°,三个内角和等于120°,不满足题意(舍去),
而当第三角为2x时,解得x=30°,2x=60°,三个内角和为150°,也不满足,
所以此题没有解.
Q
