冀教版八年级数学下册22.4《矩形》课件(共25张PPT)
文档属性
| 名称 | 冀教版八年级数学下册22.4《矩形》课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-02 09:40:02 | ||
图片预览




文档简介
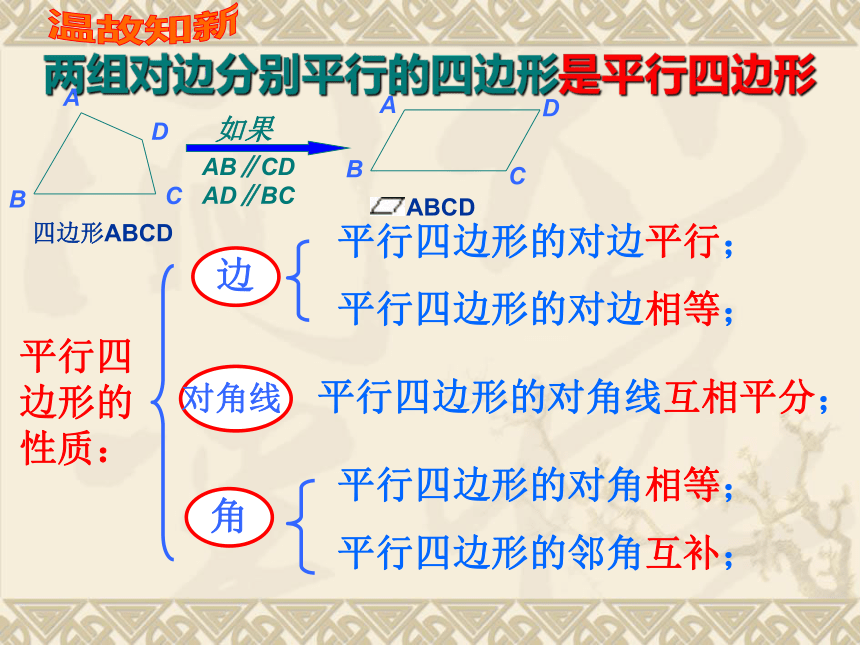
课件25张PPT。矩 形两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新一个角是
直角两组对边
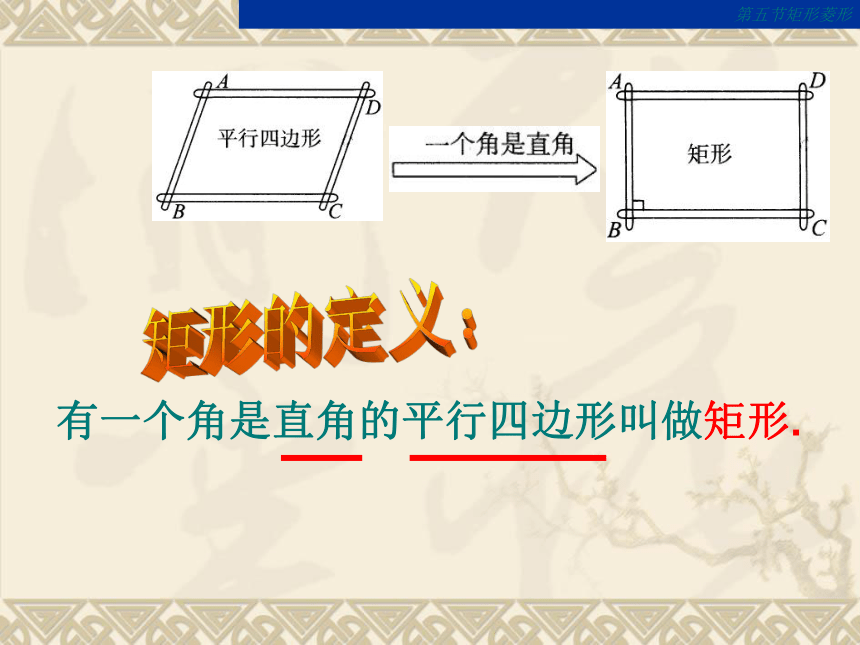
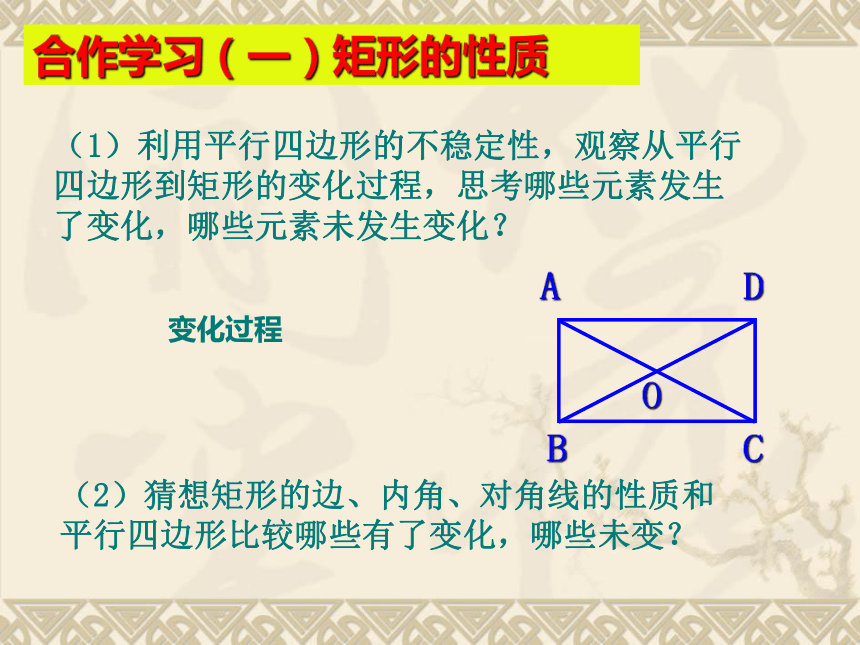
分别平行矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也,这堂课我们就来研究一种恃殊的平行四边形—— 矩形第五节矩形菱形有一个角是直角的平行四边形叫做矩形.矩形的定义:合作学习(一)矩形的性质(1)利用平行四边形的不稳定性,观察从平行
四边形到矩形的变化过程,思考哪些元素发生
了变化,哪些元素未发生变化?变化过程
四个角都是直
角对边平行且相
等对角线互相平
分且相等性质1:矩形的四个角都是直角;已知:四边形ABCD是矩形,∠C= 90°
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是矩形, 令∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
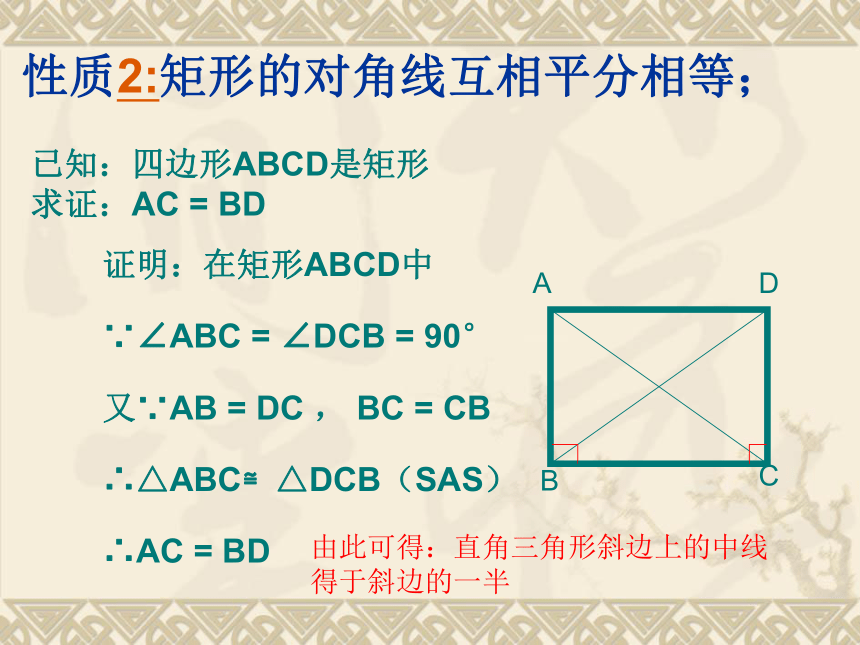
即∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
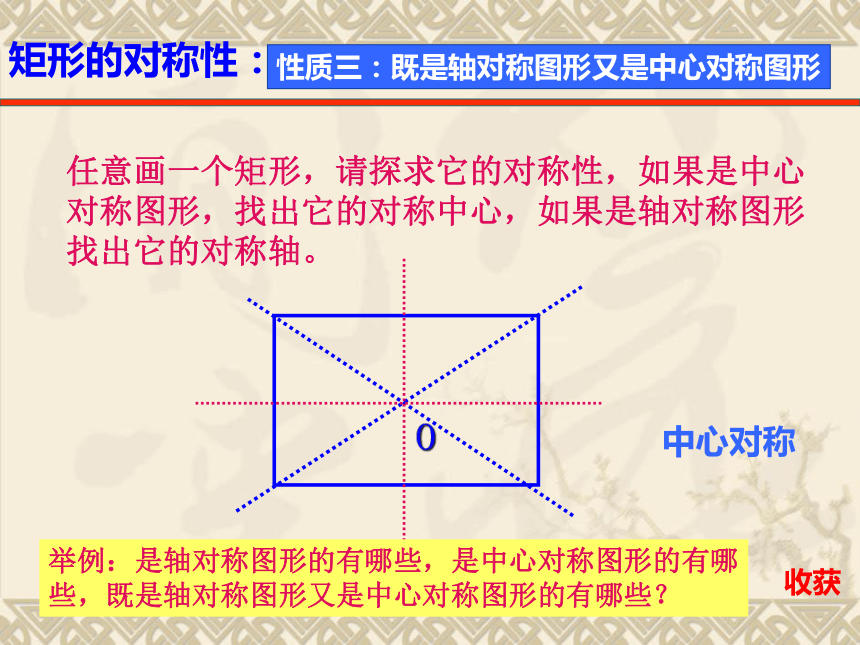
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB(SAS)∴AC = BD性质2:矩形的对角线互相平分相等;由此可得:直角三角形斜边上的中线得于斜边的一半矩形的对称性:任意画一个矩形,请探求它的对称性,如果是中心
对称图形,找出它的对称中心,如果是轴对称图形
找出它的对称轴。O举例:是轴对称图形的有哪些,是中心对称图形的有哪
些,既是轴对称图形又是中心对称图形的有哪些? 性质三:既是轴对称图形又是中心对称图形中心对称收获运用性质,提高能力问题1:(1)根据矩形的上述性质,
你能发现OA、OB、OC、OD有什么
关系?(2)由OA=OB=OC=OD可知图中有几
个等腰三角形?这些三角形全等吗?
面积相等吗?(3)若已知BC=8,O到BC的距离为3,求矩形的
面积,周长,对角线的长度。解:OA=OB=OC=OD∵在矩形ABCD中∴AC=BD,OA=OC,OD=OB
∴ OA=OB=OC=OD
(3)若∠AOD=120度,AB=4厘米,求矩形的对
角线长,周长,面积。问题2:如图,矩形ABCD的两条对
角线相交于点O(1)若∠AOD=120度,试判断
ΔAOB的形状。(2)若要得到ΔAOB是等边Δ,你可以添加一
个什么条件?四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°试一试1.矩形具有而平行四边形不具有的性质( )
(A)内角和是360度 (B)对角相等
(C)对边平行且相等 (D)对角线相等 2.下面性质中,矩形不一定具有的是( )
(A)对角线相等 (B)四个角相等
(C)是轴对称图形 (D)对角线垂直
3.下面图形中,既是轴对称图形,又是中心对称图形的是( )
(A)角(B)任意三角形(C)矩形(D)等腰三角形
4.由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)60度(B)45度(C)30度(D)22.5度
DDCB拓展思维:
1.如图,在矩形ABCD中,AE=BF=3,EF⊥ED交BC于点F,矩形的周长为22,
求EF的长.解:∵在矩形ABCD中,
∴∠A=∠B=90°,
∴∠AED+∠ADE=90 °
∵ EF⊥ED,
∴∠AED+ ∠BEF=90 °
∴ ∠ADE= ∠BEF
在△ADE和△BEF中
∠A=∠B(已证)∠ADE= ∠BEF(已证)AE=BF(已知)∴ △ADE≌△BEF(AAS)
∴AD=BE ∵矩形的周长为22
∴AD+AE+BE=11
∴BE=4
∴EF=5合作学习(二)矩形的识别①定义:有一个角是直角的平行四边形是矩形.
应用格式:①∵在平行四边形ABCD中,∠A=90°
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)②有三个角是直角的四边形是矩形已知:如上图, ∠A= ∠ B= ∠ C=90°,
试说明:四边形ABCD是矩形。
证明: ∵ ∠A+∠ B=90°+90°=180°
∴AC//BD
∴同理可得AB//CD
∴四边形ABCD是平行四边形(定义)
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)应用格式:∵ ∠A= ∠ B= ∠ C=90°,
∴四边形ABCD是矩形
(有三个角是直角的四边形是矩形)③对角线相等的平行四边形是矩形
说理证明:已知如图:在平行四边形ABCD中,AC=BD.试说明:四边形ABCD是矩形。
证明:∵在平行四边形ABCD中
∴AD=CB, ∠DAB+ ∠CBA=180°
在△DAB和△CBA中
∴ △DAB≌△CBA(SSS)
∴ ∠DAB= ∠CBA=90°
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)
应用格式:∵在平行四边形ABCD中,AC=BD.
∴四边形ABCD是矩形
(对角线相等的平行四边形是矩形)④对角线相等且互相平分的四边形是矩形.说理证明:
已知:四边形ABCD中,AC=BD,OA=OC,OB=OD
试说明:四边形ABCD是矩形
证明:∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
∴AD=BC,AD//BC
∴ ∠DAB+ ∠CBA=180°
在△DAB和△CBA中
∴△DAB≌△CBA(SSS)∴ ∠DAB=∠CBA=90°
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)
应用格式:∵ AC=BD,OA=OC,OB=OD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形)解:(1)∵在矩形ABCD中
∴∠BAD=∠ABC=90°
∵AE平分∠BAD
∴ ∠BAE= ∠EAD=45°
即∠1+ ∠CAD=45°
∴ ∠CAD= 45°-15°=30°
∵ AD//BC
∴ ∠2= ∠CAD =30°解:(2)∵在矩形ABCD中
∴OB=OA, ∠ABE=90°
∵ ∠BAE45°(第一问已证)
∴ ∠AEB=45 °
∴ AB=BE
又∵ ∠BAO= ∠BAE+ ∠1=60°
∴ △ OAB为等边三角形
∴AB=OB
∴BO=BE
解:(1) 在△ABC中
∵ AB=AC,AD⊥BC
∴∠BAD=∠DAC(三线合一)
∵AN平分∠MAC
∴ ∠MAE= ∠CAE
∴ ∠DAE=∠DAC+ ∠CAE
= ×180 °=90 °
∵ AD ⊥ BC CE ⊥ AN
∴ ∠ADC= ∠CAE =90°
∴ 四边形ADCE为矩形(有三个角是直角的四边形是矩形)
直角两组对边
分别平行矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也,这堂课我们就来研究一种恃殊的平行四边形—— 矩形第五节矩形菱形有一个角是直角的平行四边形叫做矩形.矩形的定义:合作学习(一)矩形的性质(1)利用平行四边形的不稳定性,观察从平行
四边形到矩形的变化过程,思考哪些元素发生
了变化,哪些元素未发生变化?变化过程
四个角都是直
角对边平行且相
等对角线互相平
分且相等性质1:矩形的四个角都是直角;已知:四边形ABCD是矩形,∠C= 90°
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是矩形, 令∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB(SAS)∴AC = BD性质2:矩形的对角线互相平分相等;由此可得:直角三角形斜边上的中线得于斜边的一半矩形的对称性:任意画一个矩形,请探求它的对称性,如果是中心
对称图形,找出它的对称中心,如果是轴对称图形
找出它的对称轴。O举例:是轴对称图形的有哪些,是中心对称图形的有哪
些,既是轴对称图形又是中心对称图形的有哪些? 性质三:既是轴对称图形又是中心对称图形中心对称收获运用性质,提高能力问题1:(1)根据矩形的上述性质,
你能发现OA、OB、OC、OD有什么
关系?(2)由OA=OB=OC=OD可知图中有几
个等腰三角形?这些三角形全等吗?
面积相等吗?(3)若已知BC=8,O到BC的距离为3,求矩形的
面积,周长,对角线的长度。解:OA=OB=OC=OD∵在矩形ABCD中∴AC=BD,OA=OC,OD=OB
∴ OA=OB=OC=OD
(3)若∠AOD=120度,AB=4厘米,求矩形的对
角线长,周长,面积。问题2:如图,矩形ABCD的两条对
角线相交于点O(1)若∠AOD=120度,试判断
ΔAOB的形状。(2)若要得到ΔAOB是等边Δ,你可以添加一
个什么条件?四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°试一试1.矩形具有而平行四边形不具有的性质( )
(A)内角和是360度 (B)对角相等
(C)对边平行且相等 (D)对角线相等 2.下面性质中,矩形不一定具有的是( )
(A)对角线相等 (B)四个角相等
(C)是轴对称图形 (D)对角线垂直
3.下面图形中,既是轴对称图形,又是中心对称图形的是( )
(A)角(B)任意三角形(C)矩形(D)等腰三角形
4.由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)60度(B)45度(C)30度(D)22.5度
DDCB拓展思维:
1.如图,在矩形ABCD中,AE=BF=3,EF⊥ED交BC于点F,矩形的周长为22,
求EF的长.解:∵在矩形ABCD中,
∴∠A=∠B=90°,
∴∠AED+∠ADE=90 °
∵ EF⊥ED,
∴∠AED+ ∠BEF=90 °
∴ ∠ADE= ∠BEF
在△ADE和△BEF中
∠A=∠B(已证)∠ADE= ∠BEF(已证)AE=BF(已知)∴ △ADE≌△BEF(AAS)
∴AD=BE ∵矩形的周长为22
∴AD+AE+BE=11
∴BE=4
∴EF=5合作学习(二)矩形的识别①定义:有一个角是直角的平行四边形是矩形.
应用格式:①∵在平行四边形ABCD中,∠A=90°
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)②有三个角是直角的四边形是矩形已知:如上图, ∠A= ∠ B= ∠ C=90°,
试说明:四边形ABCD是矩形。
证明: ∵ ∠A+∠ B=90°+90°=180°
∴AC//BD
∴同理可得AB//CD
∴四边形ABCD是平行四边形(定义)
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)应用格式:∵ ∠A= ∠ B= ∠ C=90°,
∴四边形ABCD是矩形
(有三个角是直角的四边形是矩形)③对角线相等的平行四边形是矩形
说理证明:已知如图:在平行四边形ABCD中,AC=BD.试说明:四边形ABCD是矩形。
证明:∵在平行四边形ABCD中
∴AD=CB, ∠DAB+ ∠CBA=180°
在△DAB和△CBA中
∴ △DAB≌△CBA(SSS)
∴ ∠DAB= ∠CBA=90°
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)
应用格式:∵在平行四边形ABCD中,AC=BD.
∴四边形ABCD是矩形
(对角线相等的平行四边形是矩形)④对角线相等且互相平分的四边形是矩形.说理证明:
已知:四边形ABCD中,AC=BD,OA=OC,OB=OD
试说明:四边形ABCD是矩形
证明:∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
∴AD=BC,AD//BC
∴ ∠DAB+ ∠CBA=180°
在△DAB和△CBA中
∴△DAB≌△CBA(SSS)∴ ∠DAB=∠CBA=90°
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)
应用格式:∵ AC=BD,OA=OC,OB=OD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形)解:(1)∵在矩形ABCD中
∴∠BAD=∠ABC=90°
∵AE平分∠BAD
∴ ∠BAE= ∠EAD=45°
即∠1+ ∠CAD=45°
∴ ∠CAD= 45°-15°=30°
∵ AD//BC
∴ ∠2= ∠CAD =30°解:(2)∵在矩形ABCD中
∴OB=OA, ∠ABE=90°
∵ ∠BAE45°(第一问已证)
∴ ∠AEB=45 °
∴ AB=BE
又∵ ∠BAO= ∠BAE+ ∠1=60°
∴ △ OAB为等边三角形
∴AB=OB
∴BO=BE
解:(1) 在△ABC中
∵ AB=AC,AD⊥BC
∴∠BAD=∠DAC(三线合一)
∵AN平分∠MAC
∴ ∠MAE= ∠CAE
∴ ∠DAE=∠DAC+ ∠CAE
= ×180 °=90 °
∵ AD ⊥ BC CE ⊥ AN
∴ ∠ADC= ∠CAE =90°
∴ 四边形ADCE为矩形(有三个角是直角的四边形是矩形)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
