22.1 比例线段 课时同步培优练习(含答案)2023-2024学年沪科版九年级数学上册
文档属性
| 名称 | 22.1 比例线段 课时同步培优练习(含答案)2023-2024学年沪科版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 00:00:00 | ||
图片预览



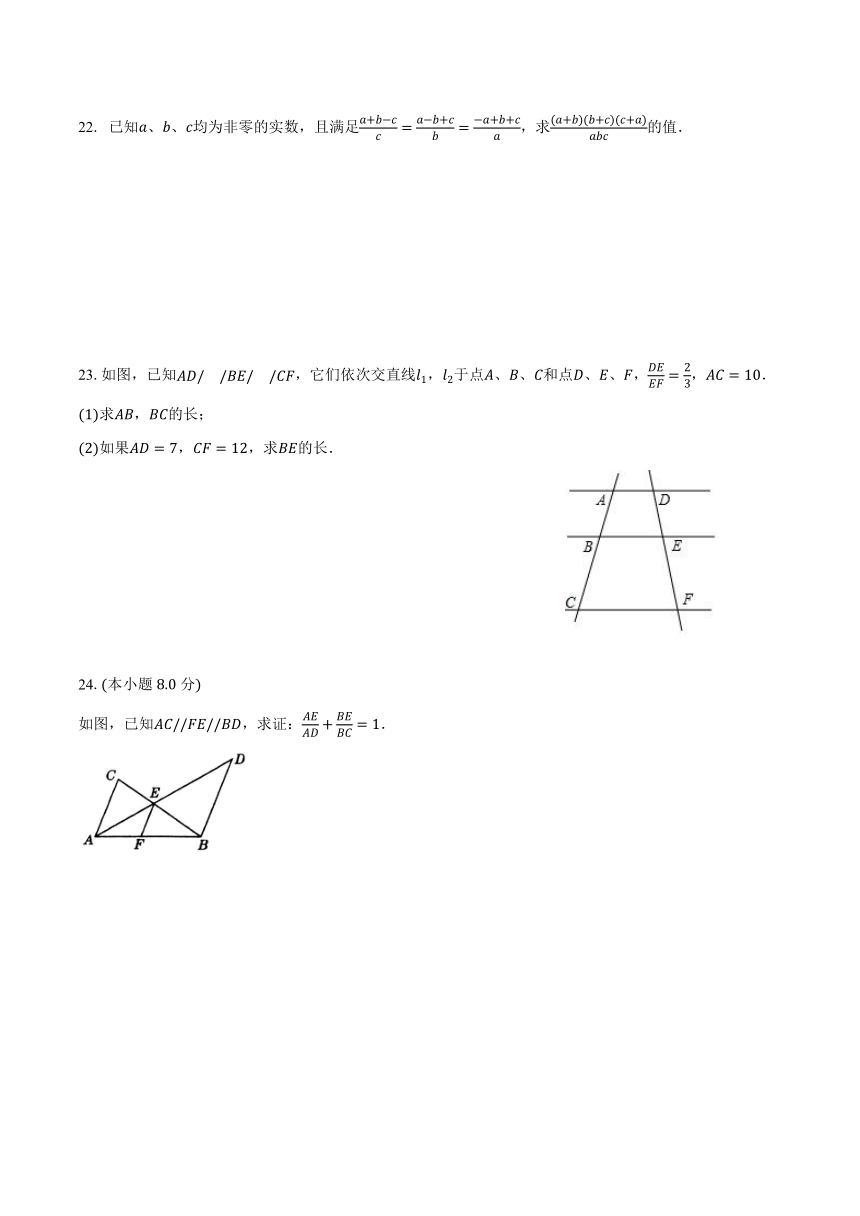
文档简介
22.1 比例线段 课时同步培优练习
一、选择题(在每小题列出的选项中,选出符合题目的一项)
1.若,则( )
A. B. C. D.
2.若,则( )
A. B. C. D.
3.若,则的值为 ( )
A. B. C. D.
4.如果,那么的值是( )
A. B. C. D.
5.如果线段、、、满足,那么下列等式不一定成立的是( )
A. B. C. D.
6.已知点是线段上的一个点,且满足,则下列式子成立的是( )
A. B. C. D.
7.我们把顶角为的等腰三角形称为“黄金三角形”,它的底与腰的比值为,如图,在中,,,平分交于点,若,则的长为( )
A. B. C. D.
8.已知点是线段的黄金分割点,且,若,则的值为( )
A. B. C. D.
9.如图,,直线,与、、分别相交于、、和点、、若,,则的长是( )
A. B. C. D.
10.如图:,,,那么的长为
A. B. C. D.
11.如图所示,中若,,则下列比例式正确的是( )
A. B. C. D.
12.如图,是的中线,点在上,,连接并延长交于点,则:的值是( )
A. : B. : C. : D. :
二、填空题
13.已知,那么______.
14.已知,那么___________;
15.已知,若,则____.
16.已知点是线段的黄金分割点,且,,那么______.
17.在小提琴的设计中,经常会引入黄金分割的概念.如图,一架小提琴中、、各部分长度的比满足,则______.
18.如图直线,直线和被,,所截,直线与三条直线分别交于点,,,直线与三条直线分别交于点,,,若,,,则的长为 .
19.如图,已知在中,点、、分别是边、、上的点,,,且::,那么:等于______.
20.如图,在中,平分,交于点,且,,交于点若,则的长是 .
三、解答题(解答应写出文字说明,证明过程或演算步骤)
21.求值:已知,求的值;已知,,求的值.
22. 已知、、均为非零的实数,且满足,求的值.
23.如图,已知,它们依次交直线,于点、、和点、、,,.
求,的长;
如果,,求的长.
24.本小题分
如图,已知,求证:.
如图,中,是的中点,在上,、交于点.已知:::,求值.
如图,在等边三角形中,点,分别在,的延长线上,且,的延长线交于点.
求的度数;
延长至点,使,连接交于点依题意补全图形,猜想线段与的数量关系,并证明.
22.1 比例线段课时同步培优练习答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18.
19.
20.
21. 解:设,则,
.
设,则,,.
,
解得.
,,.
.
22. 解:当时,
利用比例的性质化简已知等式得:,
即,,,
整理得:,,,
此时原式;
当时,可得:,,,
则原式.
综上可知,的值为或.
23. 解:,
,
,
,
,
;
如图所示:过点作交于点,交于点,
又,,
,
,
,
,
,
,
.
24. 证明:,
,
,
,
,得:,
即.
25. 解:取中点,连接,如图,
是中点,为的中点,
为的中位线,
,
,
,
.
26. 是等边三角形,
, .
.
,
.
.
,
.
即 .
补全图形,如下图:
猜想 ,理由如下:
在 上截取 ,连接 , ,
,
是等边三角形,
, ,
是等边三角形,
, ,
.
即 .
.
.
.
.
.
.
, ,
.
.
一、选择题(在每小题列出的选项中,选出符合题目的一项)
1.若,则( )
A. B. C. D.
2.若,则( )
A. B. C. D.
3.若,则的值为 ( )
A. B. C. D.
4.如果,那么的值是( )
A. B. C. D.
5.如果线段、、、满足,那么下列等式不一定成立的是( )
A. B. C. D.
6.已知点是线段上的一个点,且满足,则下列式子成立的是( )
A. B. C. D.
7.我们把顶角为的等腰三角形称为“黄金三角形”,它的底与腰的比值为,如图,在中,,,平分交于点,若,则的长为( )
A. B. C. D.
8.已知点是线段的黄金分割点,且,若,则的值为( )
A. B. C. D.
9.如图,,直线,与、、分别相交于、、和点、、若,,则的长是( )
A. B. C. D.
10.如图:,,,那么的长为
A. B. C. D.
11.如图所示,中若,,则下列比例式正确的是( )
A. B. C. D.
12.如图,是的中线,点在上,,连接并延长交于点,则:的值是( )
A. : B. : C. : D. :
二、填空题
13.已知,那么______.
14.已知,那么___________;
15.已知,若,则____.
16.已知点是线段的黄金分割点,且,,那么______.
17.在小提琴的设计中,经常会引入黄金分割的概念.如图,一架小提琴中、、各部分长度的比满足,则______.
18.如图直线,直线和被,,所截,直线与三条直线分别交于点,,,直线与三条直线分别交于点,,,若,,,则的长为 .
19.如图,已知在中,点、、分别是边、、上的点,,,且::,那么:等于______.
20.如图,在中,平分,交于点,且,,交于点若,则的长是 .
三、解答题(解答应写出文字说明,证明过程或演算步骤)
21.求值:已知,求的值;已知,,求的值.
22. 已知、、均为非零的实数,且满足,求的值.
23.如图,已知,它们依次交直线,于点、、和点、、,,.
求,的长;
如果,,求的长.
24.本小题分
如图,已知,求证:.
如图,中,是的中点,在上,、交于点.已知:::,求值.
如图,在等边三角形中,点,分别在,的延长线上,且,的延长线交于点.
求的度数;
延长至点,使,连接交于点依题意补全图形,猜想线段与的数量关系,并证明.
22.1 比例线段课时同步培优练习答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18.
19.
20.
21. 解:设,则,
.
设,则,,.
,
解得.
,,.
.
22. 解:当时,
利用比例的性质化简已知等式得:,
即,,,
整理得:,,,
此时原式;
当时,可得:,,,
则原式.
综上可知,的值为或.
23. 解:,
,
,
,
,
;
如图所示:过点作交于点,交于点,
又,,
,
,
,
,
,
,
.
24. 证明:,
,
,
,
,得:,
即.
25. 解:取中点,连接,如图,
是中点,为的中点,
为的中位线,
,
,
,
.
26. 是等边三角形,
, .
.
,
.
.
,
.
即 .
补全图形,如下图:
猜想 ,理由如下:
在 上截取 ,连接 , ,
,
是等边三角形,
, ,
是等边三角形,
, ,
.
即 .
.
.
.
.
.
.
, ,
.
.
