13.1.2 线段的垂直平分线的性质 同步训练 (含答案)人教版八年级数学上册
文档属性
| 名称 | 13.1.2 线段的垂直平分线的性质 同步训练 (含答案)人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 720.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 14:24:21 | ||
图片预览


文档简介
13.1.2线段的垂直平分线的性质 同步训练
一、单选题
1.到三角形的三个顶点距离相等的点是( )
A.三角形三条中线的交点 B.三角形三条高的交点
C.三角形三边垂直平分线的交点 D.三角形三条角平分线的交点
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列四个结论正确的个数是( )
①PA=PB ②PO平分∠APB ③OA=OB ④OP垂直平分AB.
A.1 B.2 C.3 D.4
3.如图,,点D在AB的垂直平分线上,点E在AC的垂直平分线上,则的度数是( ).
A.15° B.20° C.25° D.30°
4.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长等于( )
A.12 B.10 C.8 D.6
5.三角形纸片ABC中,∠C=90°,甲折叠纸片使点A与点B重合,压平得到的折痕长记为m;乙折叠纸片使得CA与CB所在的直线重合,压平得到的折痕长记为n,则m,n的大小关系是( )
A.m≤n B.m<n C.m≥n D.m>n
6.如图,在Rt△ABC中,∠ACB=90°,若△ACD的周长为50,DE为AB的垂直平分线,则AC+BC=( )
A.25cm B.45cm C.50cm D.55cm
7.如图,△ABC中,,,的垂直平分线交于点D,连接,则的周长为( ).
A.10 B.12 C.14 D.19
8.如图,和分别为△ABC的内角平分线和外角平分线,于点H,平分交于点F,连接.则下列结论正确的个数为( )
①;②;③;④BAC=2BEC;⑤AEH=BCF.
A.2个 B.3个 C.4个 D.5个
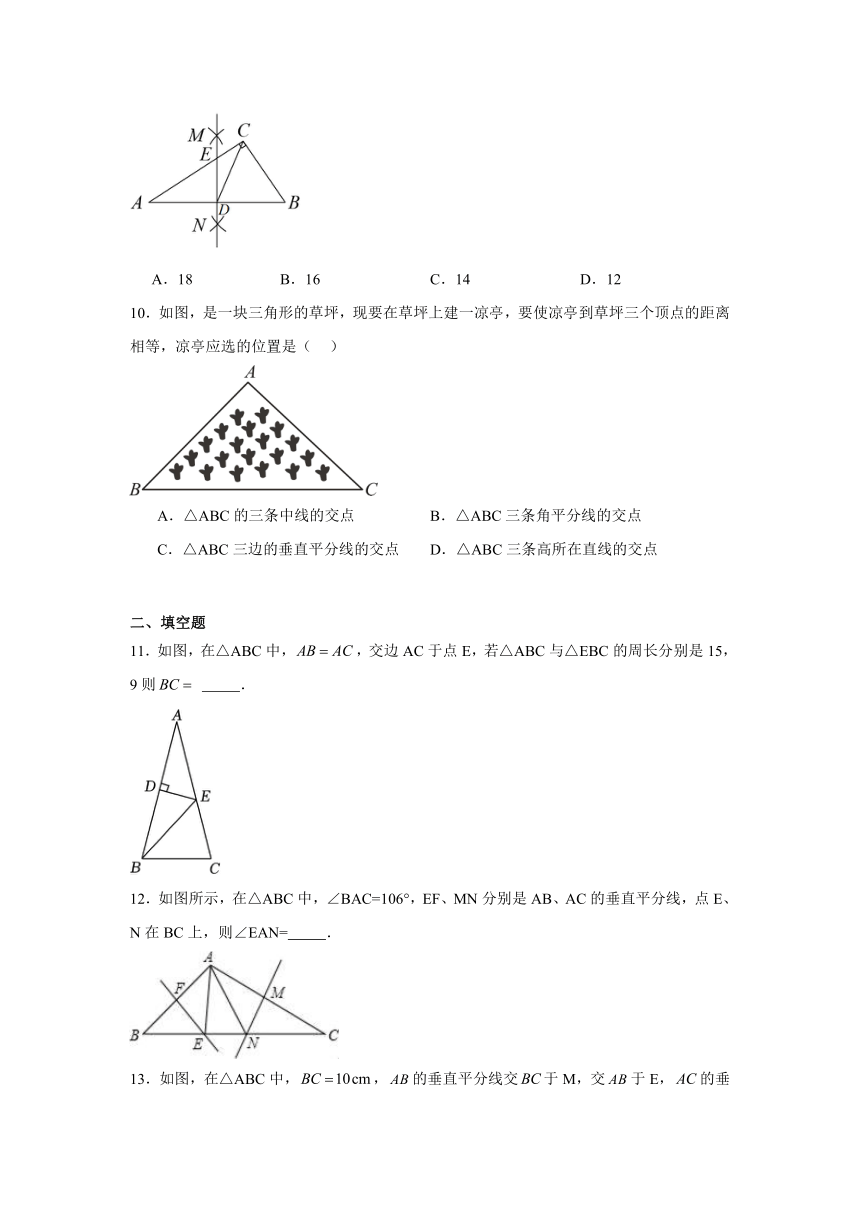
9.如图,在中,,分别以为圆心,大于长为半径画弧,两弧交于点.过的直线分别交于点,.已知,△ADE的面积为6,则△ABC的面积为( )
A.18 B.16 C.14 D.12
10.如图,是一块三角形的草坪,现要在草坪上建一凉亭,要使凉亭到草坪三个顶点的距离相等,凉亭应选的位置是( )
A.△ABC的三条中线的交点 B.△ABC三条角平分线的交点
C.△ABC三边的垂直平分线的交点 D.△ABC三条高所在直线的交点
二、填空题
11.如图,在△ABC中,,交边AC于点E,若△ABC与△EBC的周长分别是15,9则 .
12.如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN= .
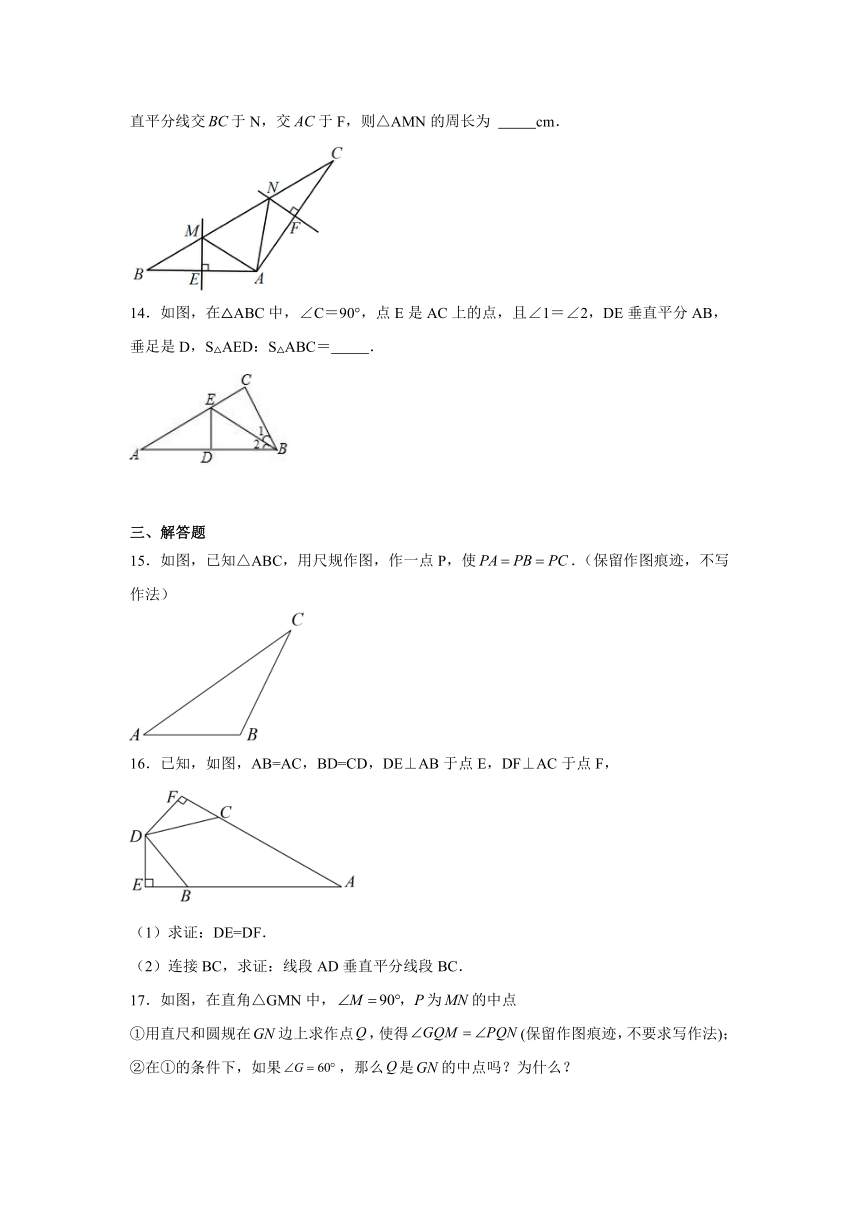
13.如图,在△ABC中,,的垂直平分线交于M,交于E,的垂直平分线交于N,交于F,则△AMN的周长为 cm.
14.如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,S△AED:S△ABC= .
三、解答题
15.如图,已知△ABC,用尺规作图,作一点P,使.(保留作图痕迹,不写作法)
16.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
(1)求证:DE=DF.
(2)连接BC,求证:线段AD垂直平分线段BC.
17.如图,在直角△GMN中,为的中点
①用直尺和圆规在边上求作点,使得(保留作图痕迹,不要求写作法);
②在①的条件下,如果,那么是的中点吗?为什么?
18.如图,在△ABC中,点D是的中点,,交的平分线于点E,,垂足为F,,交的延长线于点G,试判断线段、的数量关系,并说明理由.
19.如图所示,∠AOB内有一点P,,分别是点P关于OA,OB的对称点,交OA于点M,交OB于点N,若,求△PMN的周长.
20.如图,中,,点O为边中点,且,.
(1)请用尺规作图在上作一点D,使得.(不写作法,保留作图痕迹)
(2)在(1)的条件下,连接,求的面积.
参考答案:
1.C
2.D
3.B
4.B
5.A
6.C
7.B
8.D
9.B
10.C
11.3
12.32°
13.10
14.1:3
15.解:如图所示,点即为所求.
16.证明:(1)连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,即AD平分∠EAF,
∵DE⊥AB,DF⊥AC,
∴DE=DF;
(2)∵AB=AC,BD=CD,
∴点A、D在线段BC的垂直平分线上,
∴线段AD垂直平分线段BC.
17.解:①
② 在①的条件下,如果∠G=60°,那么Q是GN的中点,理由如下:
设PP'交GN于点K,
∵∠G=60°,∠GMN=90°,
∴∠N=90°─60°=30°,
∵点P关于GN的对称点是点P',
∴PK⊥KN,PK=P P',
∴∠PKN=90°,又∵∠N=30°,
∴PK=PN,PP'=PN,
∵P为MN的中点,
∴PM=PN,PP'=PM,
∴∠PР'M=∠PMР',
∵∠PK N=90°,∠N=30°,
∴∠NРK=90°-30°=60°,
又∵∠PP'M+∠PMP’=∠NPK,
∴∠PM P'=×60°=30°,又∵∠N=30°,
∴∠PM P'=∠N,QM=QN,
∵∠GMN=90°,∠PM P'=30°,
∴∠GMQ=90°-30°=60°,
又∵∠G=60°,
∴∠GMQ=∠G,
∴QG=QM,又∵QM=QN,
∴QG=QN,Q是GN的中点.
18.
19.5cm
20.(1)解:如图所示:点D为在上一点,使得
(2)解:如图,连接,
∵
∴
即,则
∴
∴S△ADB
∵点O为边中点
∴S△AOD=0.5S△ADB=
一、单选题
1.到三角形的三个顶点距离相等的点是( )
A.三角形三条中线的交点 B.三角形三条高的交点
C.三角形三边垂直平分线的交点 D.三角形三条角平分线的交点
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列四个结论正确的个数是( )
①PA=PB ②PO平分∠APB ③OA=OB ④OP垂直平分AB.
A.1 B.2 C.3 D.4
3.如图,,点D在AB的垂直平分线上,点E在AC的垂直平分线上,则的度数是( ).
A.15° B.20° C.25° D.30°
4.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长等于( )
A.12 B.10 C.8 D.6
5.三角形纸片ABC中,∠C=90°,甲折叠纸片使点A与点B重合,压平得到的折痕长记为m;乙折叠纸片使得CA与CB所在的直线重合,压平得到的折痕长记为n,则m,n的大小关系是( )
A.m≤n B.m<n C.m≥n D.m>n
6.如图,在Rt△ABC中,∠ACB=90°,若△ACD的周长为50,DE为AB的垂直平分线,则AC+BC=( )
A.25cm B.45cm C.50cm D.55cm
7.如图,△ABC中,,,的垂直平分线交于点D,连接,则的周长为( ).
A.10 B.12 C.14 D.19
8.如图,和分别为△ABC的内角平分线和外角平分线,于点H,平分交于点F,连接.则下列结论正确的个数为( )
①;②;③;④BAC=2BEC;⑤AEH=BCF.
A.2个 B.3个 C.4个 D.5个
9.如图,在中,,分别以为圆心,大于长为半径画弧,两弧交于点.过的直线分别交于点,.已知,△ADE的面积为6,则△ABC的面积为( )
A.18 B.16 C.14 D.12
10.如图,是一块三角形的草坪,现要在草坪上建一凉亭,要使凉亭到草坪三个顶点的距离相等,凉亭应选的位置是( )
A.△ABC的三条中线的交点 B.△ABC三条角平分线的交点
C.△ABC三边的垂直平分线的交点 D.△ABC三条高所在直线的交点
二、填空题
11.如图,在△ABC中,,交边AC于点E,若△ABC与△EBC的周长分别是15,9则 .
12.如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN= .
13.如图,在△ABC中,,的垂直平分线交于M,交于E,的垂直平分线交于N,交于F,则△AMN的周长为 cm.
14.如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,S△AED:S△ABC= .
三、解答题
15.如图,已知△ABC,用尺规作图,作一点P,使.(保留作图痕迹,不写作法)
16.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
(1)求证:DE=DF.
(2)连接BC,求证:线段AD垂直平分线段BC.
17.如图,在直角△GMN中,为的中点
①用直尺和圆规在边上求作点,使得(保留作图痕迹,不要求写作法);
②在①的条件下,如果,那么是的中点吗?为什么?
18.如图,在△ABC中,点D是的中点,,交的平分线于点E,,垂足为F,,交的延长线于点G,试判断线段、的数量关系,并说明理由.
19.如图所示,∠AOB内有一点P,,分别是点P关于OA,OB的对称点,交OA于点M,交OB于点N,若,求△PMN的周长.
20.如图,中,,点O为边中点,且,.
(1)请用尺规作图在上作一点D,使得.(不写作法,保留作图痕迹)
(2)在(1)的条件下,连接,求的面积.
参考答案:
1.C
2.D
3.B
4.B
5.A
6.C
7.B
8.D
9.B
10.C
11.3
12.32°
13.10
14.1:3
15.解:如图所示,点即为所求.
16.证明:(1)连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,即AD平分∠EAF,
∵DE⊥AB,DF⊥AC,
∴DE=DF;
(2)∵AB=AC,BD=CD,
∴点A、D在线段BC的垂直平分线上,
∴线段AD垂直平分线段BC.
17.解:①
② 在①的条件下,如果∠G=60°,那么Q是GN的中点,理由如下:
设PP'交GN于点K,
∵∠G=60°,∠GMN=90°,
∴∠N=90°─60°=30°,
∵点P关于GN的对称点是点P',
∴PK⊥KN,PK=P P',
∴∠PKN=90°,又∵∠N=30°,
∴PK=PN,PP'=PN,
∵P为MN的中点,
∴PM=PN,PP'=PM,
∴∠PР'M=∠PMР',
∵∠PK N=90°,∠N=30°,
∴∠NРK=90°-30°=60°,
又∵∠PP'M+∠PMP’=∠NPK,
∴∠PM P'=×60°=30°,又∵∠N=30°,
∴∠PM P'=∠N,QM=QN,
∵∠GMN=90°,∠PM P'=30°,
∴∠GMQ=90°-30°=60°,
又∵∠G=60°,
∴∠GMQ=∠G,
∴QG=QM,又∵QM=QN,
∴QG=QN,Q是GN的中点.
18.
19.5cm
20.(1)解:如图所示:点D为在上一点,使得
(2)解:如图,连接,
∵
∴
即,则
∴
∴S△ADB
∵点O为边中点
∴S△AOD=0.5S△ADB=
