24.2.1点和圆的位置关系强化训练(含答案)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 24.2.1点和圆的位置关系强化训练(含答案)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 357.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 11:21:45 | ||
图片预览

文档简介
24.2.1点和圆的位置关系
一、单选题
1.在直角坐标系中,圆心为坐标原点,⊙O的半径为5,则与⊙O的位置关系为( )
A.点P在⊙O上 B.点P在⊙O外 C.点P在⊙O内 D.无法确定
2.用反证法证明命题“四边形中,至少有一个内角大于或等于”时,首先应假设( )
A.四个内角都小于 B.至少有一个内角不大于
C.至多有一个内角大于 D.至多有一个内角不大于
3.已知直角三角形的一条直角边等于它的外接圆的半径,则这个直角三角形的面积与其外接圆的面积的比为( )
A.:2π B.:4π C.:π D.2:π
4.如图,点A、B、C在同一直线上,点D在直线AB之外,过这四个点中的任意三个点,能画圆的个数为( )
A.1个 B.2个 C.3个 D.4个
5.下列说法正确的是( )
A.过平面内的三点可以确定一个圆 B.相等的圆周角所对的弧相等
C.圆内接菱形是正方形 D.平分弦的直径垂直弦.
6.在中,,,是的中点,以为圆心,长为半径作圆,则,,,四点中,在圆内的有( )
A.4个 B.3个 C.2个 D.1个
7.过三点A(2,2),B(6,2),C(4,4)的圆的圆心坐标为( )
A.(4,) B.(4,2) C.(5,) D.(5,2)
8.平面内一点离上的点最近距离为,离上的点最远距离为,则的半径为( )
A. B.或 C. D.或
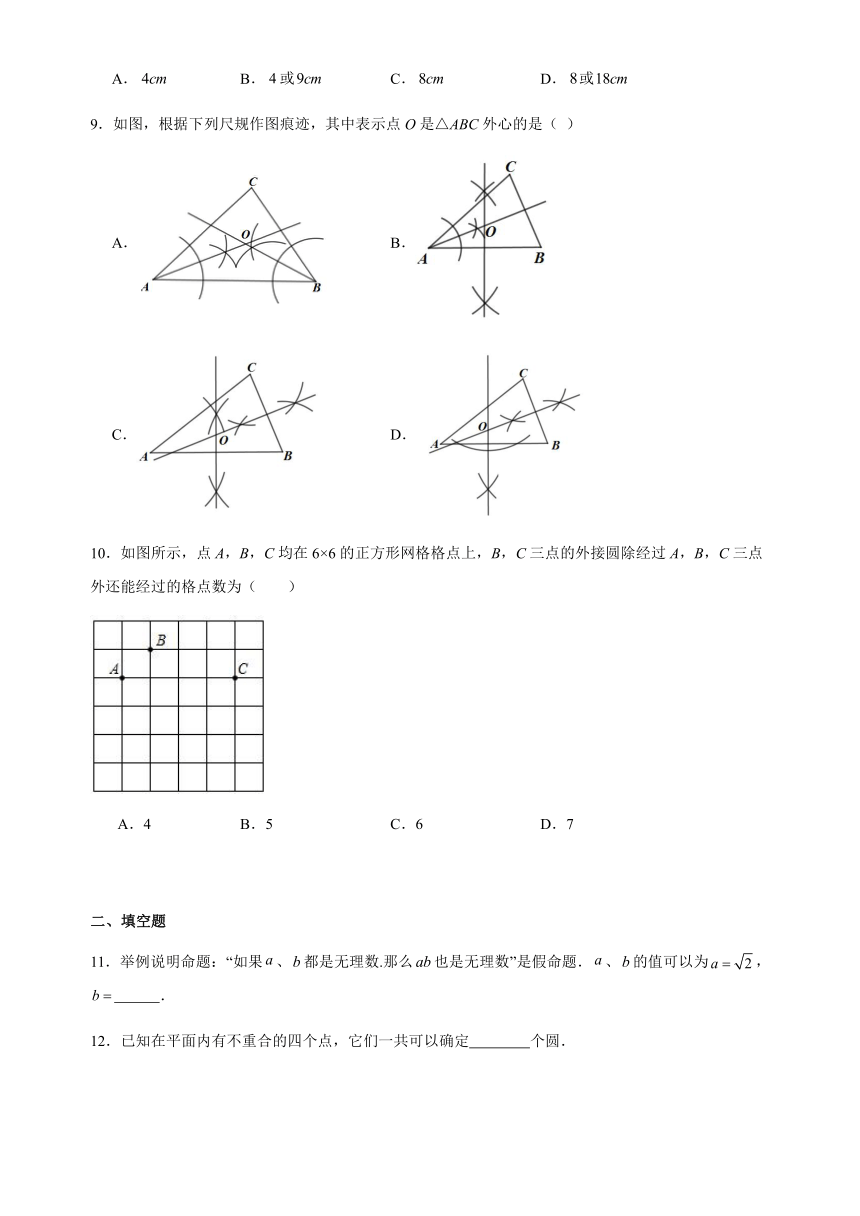
9.如图,根据下列尺规作图痕迹,其中表示点O是△ABC外心的是( )
A. B.
C. D.
10.如图所示,点A,B,C均在6×6的正方形网格格点上,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为( )
A.4 B.5 C.6 D.7
二、填空题
11.举例说明命题:“如果、都是无理数.那么也是无理数”是假命题.、的值可以为, .
12.已知在平面内有不重合的四个点,它们一共可以确定 个圆.
13.已知正ABC的边长为6,那么能够完全覆盖这个正ABC的最小圆的半径是 .
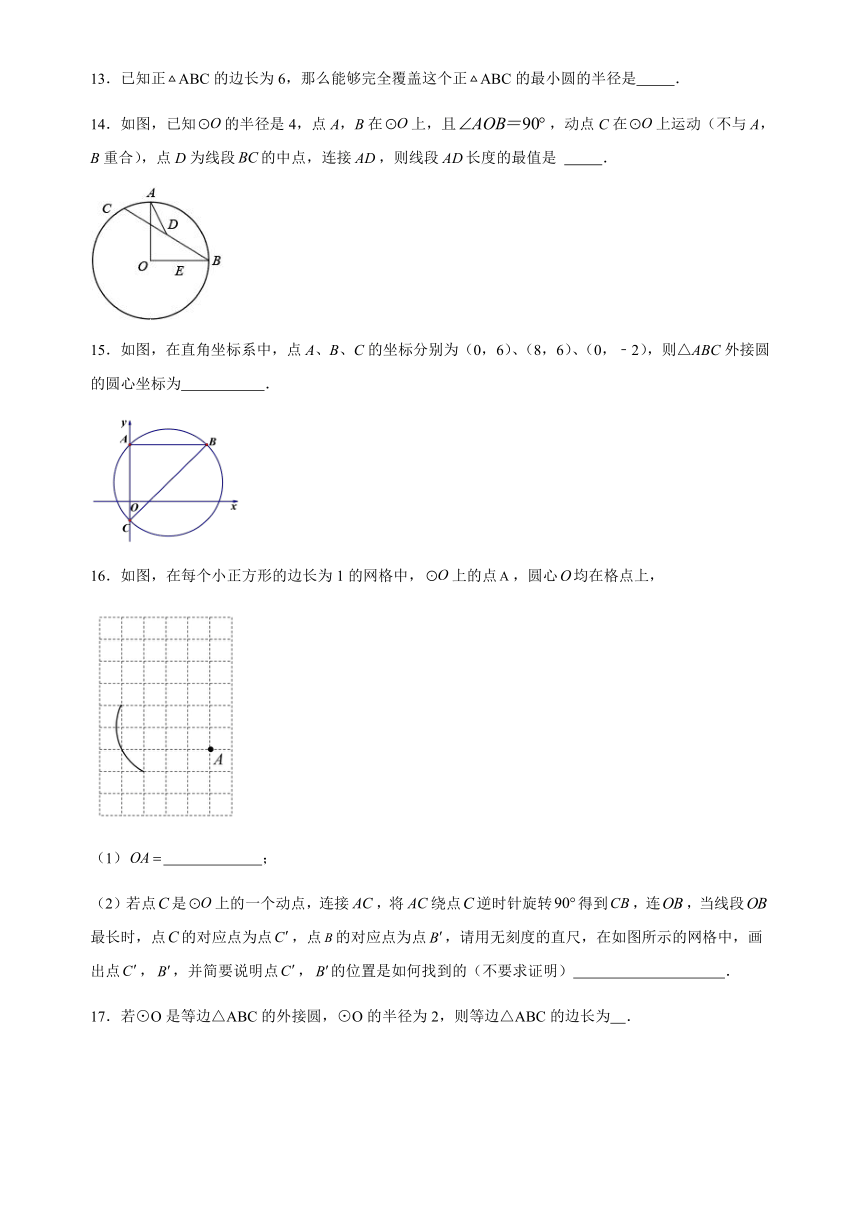
14.如图,已知的半径是4,点A,B在上,且,动点C在上运动(不与A,B重合),点D为线段的中点,连接,则线段长度的最值是 .
15.如图,在直角坐标系中,点A、B、C的坐标分别为(0,6)、(8,6)、(0,﹣2),则△ABC外接圆的圆心坐标为 .
16.如图,在每个小正方形的边长为1的网格中,上的点,圆心均在格点上,
(1) ;
(2)若点是上的一个动点,连接,将绕点逆时针旋转得到,连,当线段最长时,点的对应点为点,点的对应点为点,请用无刻度的直尺,在如图所示的网格中,画出点,,并简要说明点,的位置是如何找到的(不要求证明) .
17.若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为 .
三、解答题
18.如图,已知弧,利用直尺和圆规作弧所在的圆的圆心O,(要求保留作图痕迹)
19.如图,在平面直角坐标系中,有一圆弧经过三个点A、B、C,且点A、B、C的坐标分别为A(0,4)、B(-4,4)、C(-6,2).
(1)该圆弧所在圆的圆心的坐标为________;
(2)的半径为________;
(3)点在________(填内、外、上).
(4)点到上最近的点的距离为________;
20.小明和小华正在练习投铅球,铅球场地分为五个区域:以内,以外.小明投了,小华投了,他们投的球分别落在哪个区域内?
21.(1)如图1,和中,___________.
从下列4个信息“①,②,③BD平分,④”中,选取两个将其序号填写在横线上,使得结论成立,并说明理由.
(2)如图2,已知3个点,只用圆规作出半径为OM的与点M,N所在直线的另一个交点(不写作法,保留作图痕迹).
参考答案:
1.A
2.A
3.A
4.C
5.C
6.C
7.B
8.B
9.C
10.B
11.(答案不唯一
12.或或或
13.2
14.
15.(4,2)
16. 作直径的垂直平分线交半圆于,连接,则在以为圆心,为半径的圆上运动,直径的垂直平分线交于,过作的垂线交于,当E,O,三点共线时,最长,则点即为所求.
17.
19.(1)(2)(3)内(4)
20.小明投的球落在5~6m区域内,小华投的球落在6~7m区域内.
21.①③或①④或②③
一、单选题
1.在直角坐标系中,圆心为坐标原点,⊙O的半径为5,则与⊙O的位置关系为( )
A.点P在⊙O上 B.点P在⊙O外 C.点P在⊙O内 D.无法确定
2.用反证法证明命题“四边形中,至少有一个内角大于或等于”时,首先应假设( )
A.四个内角都小于 B.至少有一个内角不大于
C.至多有一个内角大于 D.至多有一个内角不大于
3.已知直角三角形的一条直角边等于它的外接圆的半径,则这个直角三角形的面积与其外接圆的面积的比为( )
A.:2π B.:4π C.:π D.2:π
4.如图,点A、B、C在同一直线上,点D在直线AB之外,过这四个点中的任意三个点,能画圆的个数为( )
A.1个 B.2个 C.3个 D.4个
5.下列说法正确的是( )
A.过平面内的三点可以确定一个圆 B.相等的圆周角所对的弧相等
C.圆内接菱形是正方形 D.平分弦的直径垂直弦.
6.在中,,,是的中点,以为圆心,长为半径作圆,则,,,四点中,在圆内的有( )
A.4个 B.3个 C.2个 D.1个
7.过三点A(2,2),B(6,2),C(4,4)的圆的圆心坐标为( )
A.(4,) B.(4,2) C.(5,) D.(5,2)
8.平面内一点离上的点最近距离为,离上的点最远距离为,则的半径为( )
A. B.或 C. D.或
9.如图,根据下列尺规作图痕迹,其中表示点O是△ABC外心的是( )
A. B.
C. D.
10.如图所示,点A,B,C均在6×6的正方形网格格点上,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为( )
A.4 B.5 C.6 D.7
二、填空题
11.举例说明命题:“如果、都是无理数.那么也是无理数”是假命题.、的值可以为, .
12.已知在平面内有不重合的四个点,它们一共可以确定 个圆.
13.已知正ABC的边长为6,那么能够完全覆盖这个正ABC的最小圆的半径是 .
14.如图,已知的半径是4,点A,B在上,且,动点C在上运动(不与A,B重合),点D为线段的中点,连接,则线段长度的最值是 .
15.如图,在直角坐标系中,点A、B、C的坐标分别为(0,6)、(8,6)、(0,﹣2),则△ABC外接圆的圆心坐标为 .
16.如图,在每个小正方形的边长为1的网格中,上的点,圆心均在格点上,
(1) ;
(2)若点是上的一个动点,连接,将绕点逆时针旋转得到,连,当线段最长时,点的对应点为点,点的对应点为点,请用无刻度的直尺,在如图所示的网格中,画出点,,并简要说明点,的位置是如何找到的(不要求证明) .
17.若⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为 .
三、解答题
18.如图,已知弧,利用直尺和圆规作弧所在的圆的圆心O,(要求保留作图痕迹)
19.如图,在平面直角坐标系中,有一圆弧经过三个点A、B、C,且点A、B、C的坐标分别为A(0,4)、B(-4,4)、C(-6,2).
(1)该圆弧所在圆的圆心的坐标为________;
(2)的半径为________;
(3)点在________(填内、外、上).
(4)点到上最近的点的距离为________;
20.小明和小华正在练习投铅球,铅球场地分为五个区域:以内,以外.小明投了,小华投了,他们投的球分别落在哪个区域内?
21.(1)如图1,和中,___________.
从下列4个信息“①,②,③BD平分,④”中,选取两个将其序号填写在横线上,使得结论成立,并说明理由.
(2)如图2,已知3个点,只用圆规作出半径为OM的与点M,N所在直线的另一个交点(不写作法,保留作图痕迹).
参考答案:
1.A
2.A
3.A
4.C
5.C
6.C
7.B
8.B
9.C
10.B
11.(答案不唯一
12.或或或
13.2
14.
15.(4,2)
16. 作直径的垂直平分线交半圆于,连接,则在以为圆心,为半径的圆上运动,直径的垂直平分线交于,过作的垂线交于,当E,O,三点共线时,最长,则点即为所求.
17.
19.(1)(2)(3)内(4)
20.小明投的球落在5~6m区域内,小华投的球落在6~7m区域内.
21.①③或①④或②③
同课章节目录
