1.1.2探索勾股定理(第2)课时 课件(共26张PPT) 2023-2024学年北师大版八年级数学上册
文档属性
| 名称 | 1.1.2探索勾股定理(第2)课时 课件(共26张PPT) 2023-2024学年北师大版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 890.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 11:26:56 | ||
图片预览




文档简介
(共26张PPT)
第一节 探索勾股定理(2)
第一章 勾股定理
北师大版 数学 八年级 上册
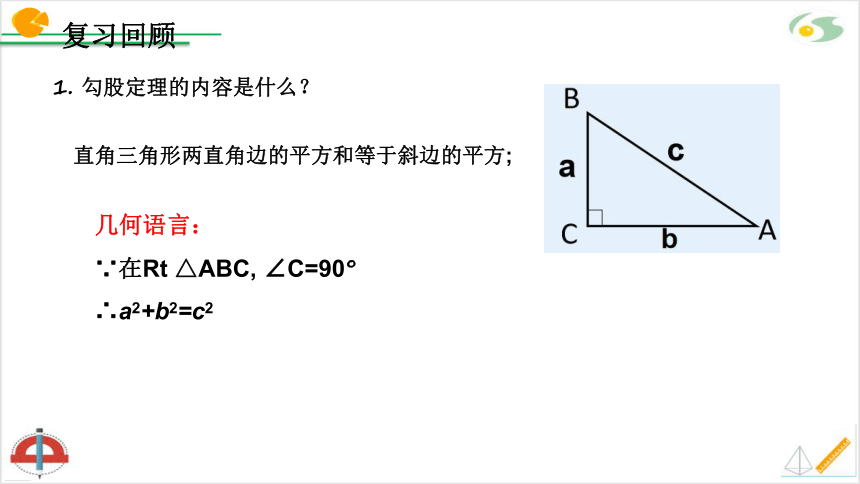
几何语言:
∵在Rt △ABC, ∠C=90°
∴a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方;
复习回顾
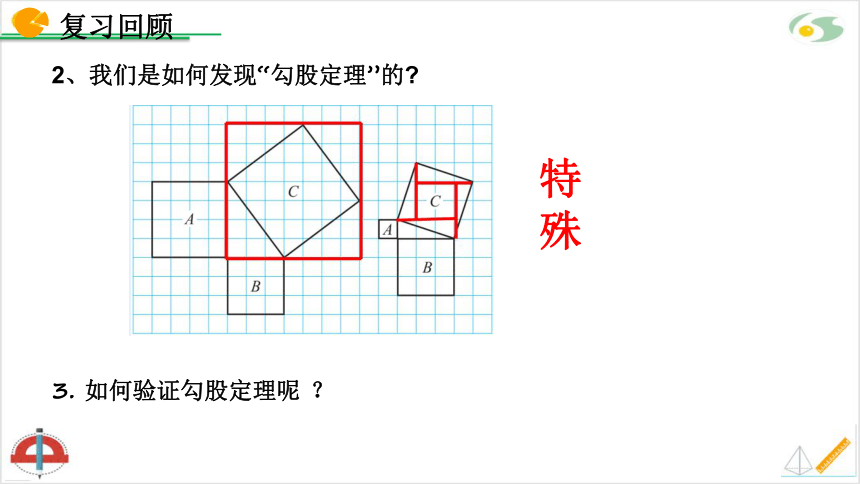
1. 勾股定理的内容是什么?
2、我们是如何发现“勾股定理”的
特殊
复习回顾
3. 如何验证勾股定理呢 ?
1.掌握用面积法如何验证勾股定理,并能应用勾股定理解决一些实际问题.
2.经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想.
学习目标
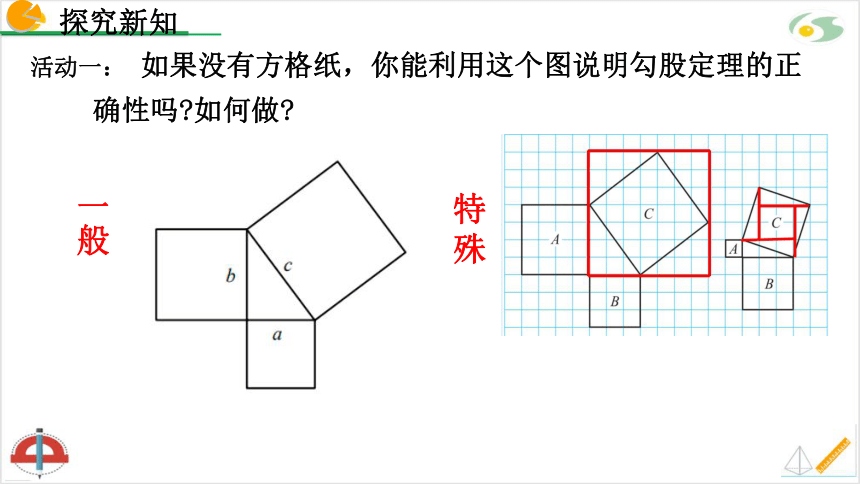
如果没有方格纸,你能利用这个图说明勾股定理的正确性吗 如何做
探究新知
一般
活动一:
特殊
割
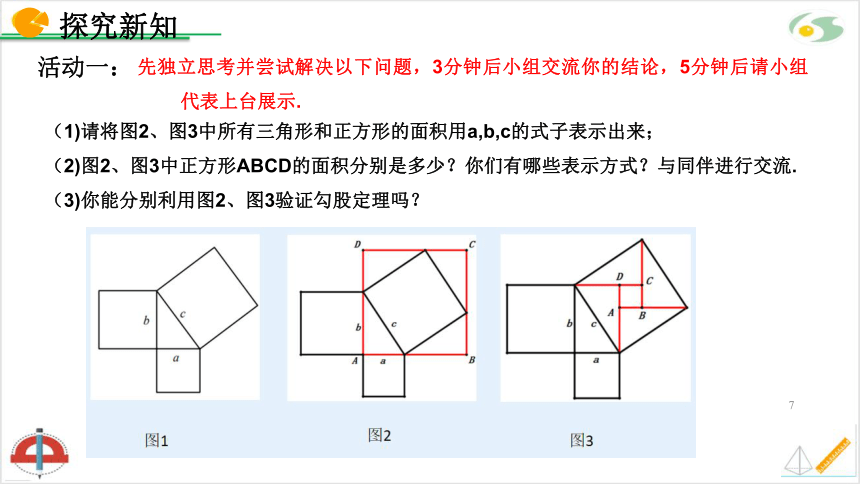
小明受到上一节课的启发,对图1中的大正方形进行割补,得到图2,图3.
补
图1
图2
图3
探究新知
活动一:
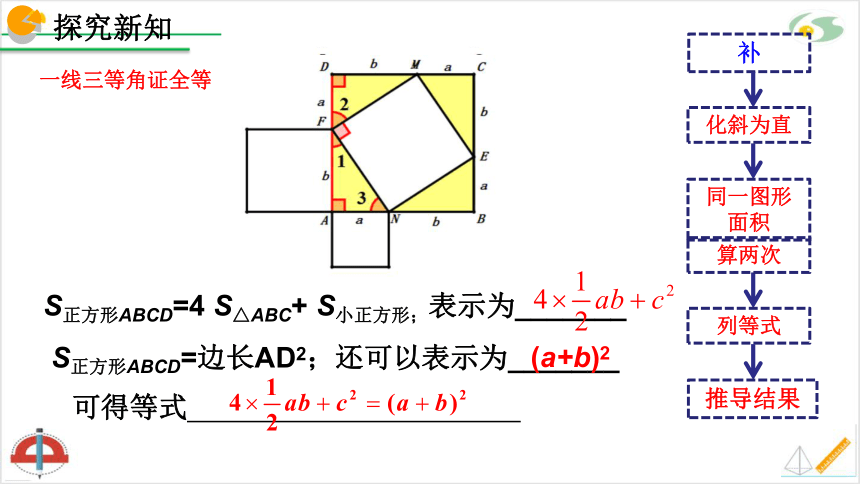
(1)请将图2、图3中所有三角形和正方形的面积用a,b,c的式子表示出来;
(2)图2、图3中正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流.
(3)你能分别利用图2、图3验证勾股定理吗?
7
探究新知
活动一:
先独立思考并尝试解决以下问题,3分钟后小组交流你的结论,5分钟后请小组代表上台展示.
S正方形ABCD=4 S△ABC+ S小正方形;表示为_______
S正方形ABCD=边长AD2;还可以表示为_______
可得等式
探究新知
(a+b)2
补
化斜为直
同一图形
面积
算两次
列等式
一线三等角证全等
推导结果
探究新知
割
化斜为直
同一图形
面积
算两次
列等式
=c2
S正方形MENF
所以 a2+b2=c2 .
=
S正方形MENF
一线三等角证全等
推导结果
应用新知
跟踪练习1:
根据前面的图形和方法,你还能用下图中其他图形验证勾股定理吗?从下列四个图形中任选一个,证明勾股定理;
直接求
间接求
总结归纳
验证勾股定理的
思路和方法
探究新知
割或补
算两次
列等式化简
同一图形面积
得结论
构造图形
a
b
c
①
②
③
④
⑤
“无字的证明”
中国的
“青朱出入图”
漫画勾股世界
请仔细观察图形变化过程,你能从中发现验证勾股定理奥秘?
拓展视野
a
b
c
A
B
C
D
E
F
O
漫画勾股世界
意大利著名画家达·芬奇的证法
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
证明:
所以a2+b2=c2 .
漫画勾股世界
请仔细观察图形变化过程,你能从中发现验证勾股定理奥秘吗?
“无字的证明”
我方侦察员小王在距离东西向公路400m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
活动二: 勾股定理的应用
已知量:AC=400m, AB=500m,∠ACB=90°;
从C到B 汽车的运动时间为10s;
未知量:BC长、汽车运动速度
数量关系:速度=路程÷时间
应用定理
即它行驶的速度为108 km/h.
总结:在实际问题中,可以根据问题中的条件构造直角三角形,从而利用勾股定理来解答.
解:
由勾股定理,可得:AB2=BC2+AC2,
即:5002=BC2+4002, 所以BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为
300×6×60=108000(m),
定理应用
飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4km处,过了20s,飞机距离这个男孩子头顶5km,飞机每小时飞行多少千米?
4km
20秒后
5km
A
B
C
跟踪练习2
在Rt△ABC中,BC2=AB2-AC2.
解:
因为AB=5,AC=4,
所以BC2=52-42.
所以BC2=9,所以BC=3,
因为 ,
所以 .
答:飞机每小时飞行540km.
议一议 判断图中三角形的三边是否满足a2+b2=c2.
锐角三角形:a2+b2 > c2
钝角三角形: a2+b2 < c2
直角三角形:a2+b2=c2
提示:用数格子的方法计算图中正方形的面积.
探究新知
A的面积 B的面积 C的面积
图1
图2
图2 图3
C
C
B
A
A
B
谈谈你本节课的收获:
1.知识方面有哪些收获和困惑?
2.学到了哪些数学思想和方法?
综合建模
验证勾股
定理及应用
拼图验证
利用面积法,将形的问题与数的问题结合起来,构造特殊图形,利用算两次面积的方法,列等式再进行化简,从理论上验证了勾股定理;
应用
拼出图形
列出同一图形面积的表达式
找出相等关系
课堂小结
步
骤
恒等变形
导出勾股定理
思
路
1.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A B C D
2.如图,一个长为2.5 m的梯子,一端放在离墙脚1.5 m处,另一端靠墙,则梯子顶端距离墙脚( )
A.0.2 m B.0.4 m C.2 m D.4 m
3.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
4.两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,
这只小鸟至少要飞多少米?
课堂检测
基础巩固题
B
C
A
4.两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米?
思路:先根据题意画出图形,然后添加辅助线,构造直角三角形,再利用勾股定理解答.
课堂检测
基础巩固题
4解:根据题意画出示意图,如图所示,
两棵树的高度分别为AB=8 m,CD=2 m,
两棵树之间的距离BD=8 m,
过点C作CE⊥AB,垂足为E,连接AC.
则BE=CD=2 m,EC=BD=8 m,
AE=AB-BE=8-2=6(m).
在Rt△ACE中,由勾股定理,得AC2=AE2+EC2,
即AC2=62+82=100,所以AC=10 m.
答:这只小鸟至少要飞10 m.
课堂检测
基础巩固题
例 等腰三角形底边上的高为8cm,周长为32cm,求这个三角形的面积.
8
x
16-x
D
A
B
C
解:设这个三角形为ABC,高为AD,设BD为xcm,则AB为(16-x)cm,
由勾股定理得:x2+82=(16-x)2
即x2+64=256-32x+x2
所以x=6
素养考点 2
利用勾股定理解答面积问题
拓展提高
方法点拨:利用勾股定理解答几何问题,经常用到设未知数列方程的思想
答:这个三角形的面积为48cm2.
S△ABC=
(cm2)
课后作业
作业
内容
教材作业
课后习题:1,2,3
自主安排
学案B组5,6,7
再见
第一节 探索勾股定理(2)
第一章 勾股定理
北师大版 数学 八年级 上册
几何语言:
∵在Rt △ABC, ∠C=90°
∴a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方;
复习回顾
1. 勾股定理的内容是什么?
2、我们是如何发现“勾股定理”的
特殊
复习回顾
3. 如何验证勾股定理呢 ?
1.掌握用面积法如何验证勾股定理,并能应用勾股定理解决一些实际问题.
2.经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想.
学习目标
如果没有方格纸,你能利用这个图说明勾股定理的正确性吗 如何做
探究新知
一般
活动一:
特殊
割
小明受到上一节课的启发,对图1中的大正方形进行割补,得到图2,图3.
补
图1
图2
图3
探究新知
活动一:
(1)请将图2、图3中所有三角形和正方形的面积用a,b,c的式子表示出来;
(2)图2、图3中正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流.
(3)你能分别利用图2、图3验证勾股定理吗?
7
探究新知
活动一:
先独立思考并尝试解决以下问题,3分钟后小组交流你的结论,5分钟后请小组代表上台展示.
S正方形ABCD=4 S△ABC+ S小正方形;表示为_______
S正方形ABCD=边长AD2;还可以表示为_______
可得等式
探究新知
(a+b)2
补
化斜为直
同一图形
面积
算两次
列等式
一线三等角证全等
推导结果
探究新知
割
化斜为直
同一图形
面积
算两次
列等式
=c2
S正方形MENF
所以 a2+b2=c2 .
=
S正方形MENF
一线三等角证全等
推导结果
应用新知
跟踪练习1:
根据前面的图形和方法,你还能用下图中其他图形验证勾股定理吗?从下列四个图形中任选一个,证明勾股定理;
直接求
间接求
总结归纳
验证勾股定理的
思路和方法
探究新知
割或补
算两次
列等式化简
同一图形面积
得结论
构造图形
a
b
c
①
②
③
④
⑤
“无字的证明”
中国的
“青朱出入图”
漫画勾股世界
请仔细观察图形变化过程,你能从中发现验证勾股定理奥秘?
拓展视野
a
b
c
A
B
C
D
E
F
O
漫画勾股世界
意大利著名画家达·芬奇的证法
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
证明:
所以a2+b2=c2 .
漫画勾股世界
请仔细观察图形变化过程,你能从中发现验证勾股定理奥秘吗?
“无字的证明”
我方侦察员小王在距离东西向公路400m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
活动二: 勾股定理的应用
已知量:AC=400m, AB=500m,∠ACB=90°;
从C到B 汽车的运动时间为10s;
未知量:BC长、汽车运动速度
数量关系:速度=路程÷时间
应用定理
即它行驶的速度为108 km/h.
总结:在实际问题中,可以根据问题中的条件构造直角三角形,从而利用勾股定理来解答.
解:
由勾股定理,可得:AB2=BC2+AC2,
即:5002=BC2+4002, 所以BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为
300×6×60=108000(m),
定理应用
飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4km处,过了20s,飞机距离这个男孩子头顶5km,飞机每小时飞行多少千米?
4km
20秒后
5km
A
B
C
跟踪练习2
在Rt△ABC中,BC2=AB2-AC2.
解:
因为AB=5,AC=4,
所以BC2=52-42.
所以BC2=9,所以BC=3,
因为 ,
所以 .
答:飞机每小时飞行540km.
议一议 判断图中三角形的三边是否满足a2+b2=c2.
锐角三角形:a2+b2 > c2
钝角三角形: a2+b2 < c2
直角三角形:a2+b2=c2
提示:用数格子的方法计算图中正方形的面积.
探究新知
A的面积 B的面积 C的面积
图1
图2
图2 图3
C
C
B
A
A
B
谈谈你本节课的收获:
1.知识方面有哪些收获和困惑?
2.学到了哪些数学思想和方法?
综合建模
验证勾股
定理及应用
拼图验证
利用面积法,将形的问题与数的问题结合起来,构造特殊图形,利用算两次面积的方法,列等式再进行化简,从理论上验证了勾股定理;
应用
拼出图形
列出同一图形面积的表达式
找出相等关系
课堂小结
步
骤
恒等变形
导出勾股定理
思
路
1.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )
A B C D
2.如图,一个长为2.5 m的梯子,一端放在离墙脚1.5 m处,另一端靠墙,则梯子顶端距离墙脚( )
A.0.2 m B.0.4 m C.2 m D.4 m
3.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
4.两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,
这只小鸟至少要飞多少米?
课堂检测
基础巩固题
B
C
A
4.两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米?
思路:先根据题意画出图形,然后添加辅助线,构造直角三角形,再利用勾股定理解答.
课堂检测
基础巩固题
4解:根据题意画出示意图,如图所示,
两棵树的高度分别为AB=8 m,CD=2 m,
两棵树之间的距离BD=8 m,
过点C作CE⊥AB,垂足为E,连接AC.
则BE=CD=2 m,EC=BD=8 m,
AE=AB-BE=8-2=6(m).
在Rt△ACE中,由勾股定理,得AC2=AE2+EC2,
即AC2=62+82=100,所以AC=10 m.
答:这只小鸟至少要飞10 m.
课堂检测
基础巩固题
例 等腰三角形底边上的高为8cm,周长为32cm,求这个三角形的面积.
8
x
16-x
D
A
B
C
解:设这个三角形为ABC,高为AD,设BD为xcm,则AB为(16-x)cm,
由勾股定理得:x2+82=(16-x)2
即x2+64=256-32x+x2
所以x=6
素养考点 2
利用勾股定理解答面积问题
拓展提高
方法点拨:利用勾股定理解答几何问题,经常用到设未知数列方程的思想
答:这个三角形的面积为48cm2.
S△ABC=
(cm2)
课后作业
作业
内容
教材作业
课后习题:1,2,3
自主安排
学案B组5,6,7
再见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
