复数代数形式的加减运算及其几何意义
文档属性
| 名称 | 复数代数形式的加减运算及其几何意义 |  | |
| 格式 | rar | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-12 22:51:00 | ||
图片预览





文档简介
课件24张PPT。人教A 版高中数学选修1-2
多媒体课件多思、创新、融合复数代数形式的四则运算
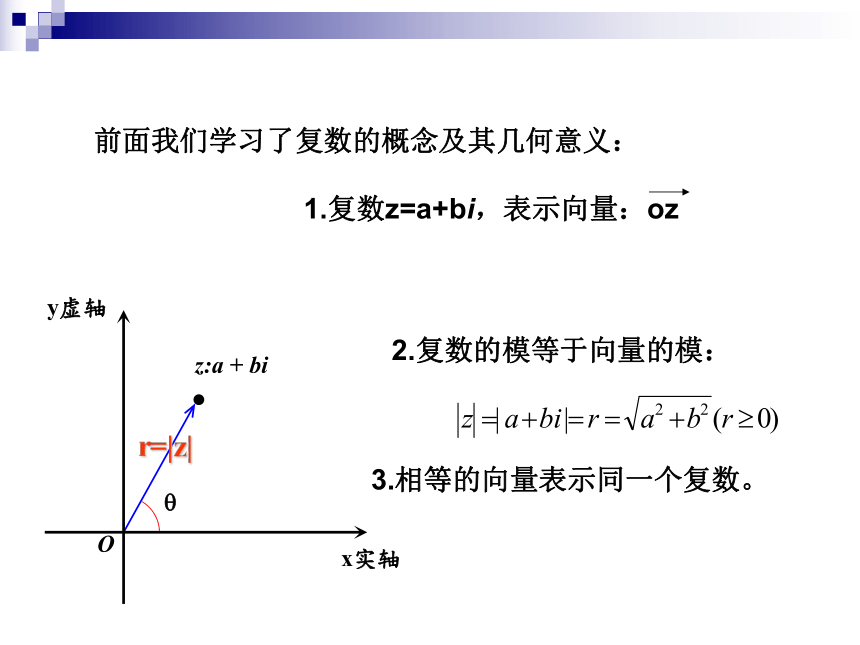
及其几何意义前面我们学习了复数的概念及其几何意义:3.相等的向量表示同一个复数。下面我们就来进一步讨论复数的运算性质规定1:复数的加法规则:z1=a+bi,z2=c+di是任意的两个复数,那么
(a+bi)+(c+di)=(a+c)+(b+d)i
因此,两个复数的和仍然是一个确定的复数复数的加法满足交换律和结合律吗?1.加法的代数运算:设,z1,z2,z3∈R,有:z1+z2=z2+z1
(z1+z2)+z3=z1+(z2+z3)(交换律)
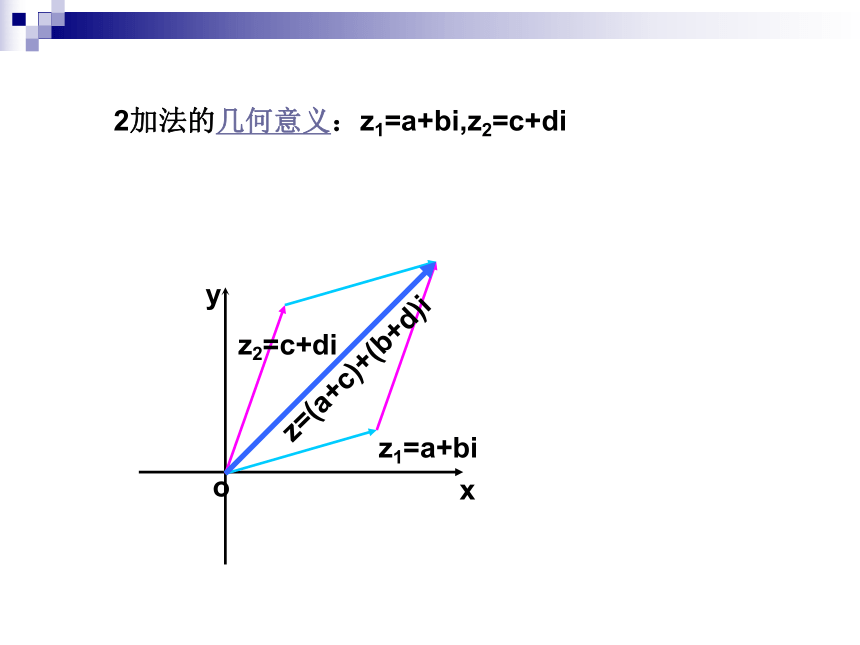
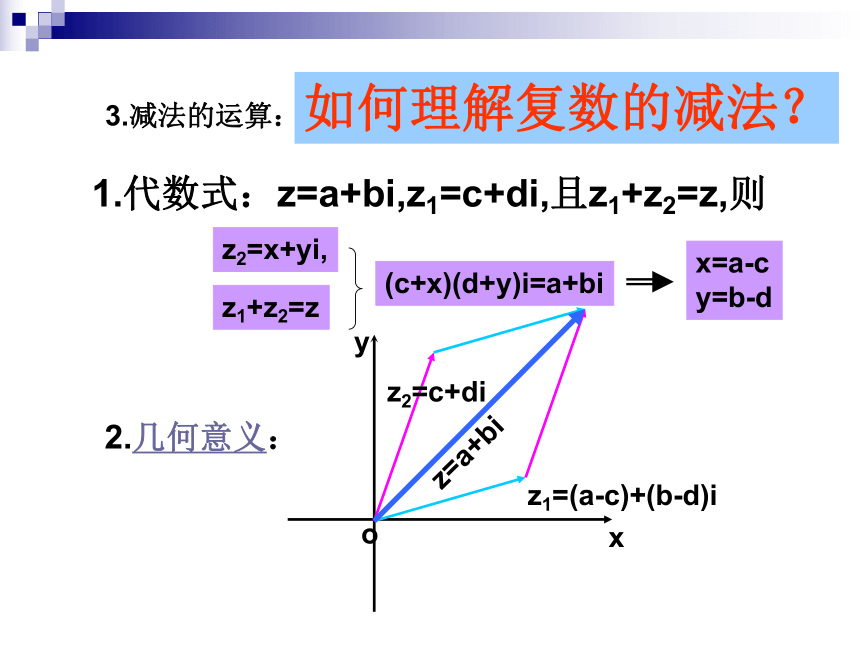
(结合律)2加法的几何意义:z1=a+bi,z2=c+di3.减法的运算:如何理解复数的减法?1.代数式:z=a+bi,z1=c+di,且z1+z2=z,则z2=x+yi,z1+z2=z(c+x)(d+y)i=a+bix=a-c
y=b-d2.几何意义:例1.计算(5-6i)+(-2-i)-(3+4i)解 原式=[5+(-2)-(3)]+[(-6)+(-1)-4]i=0+(-11)i
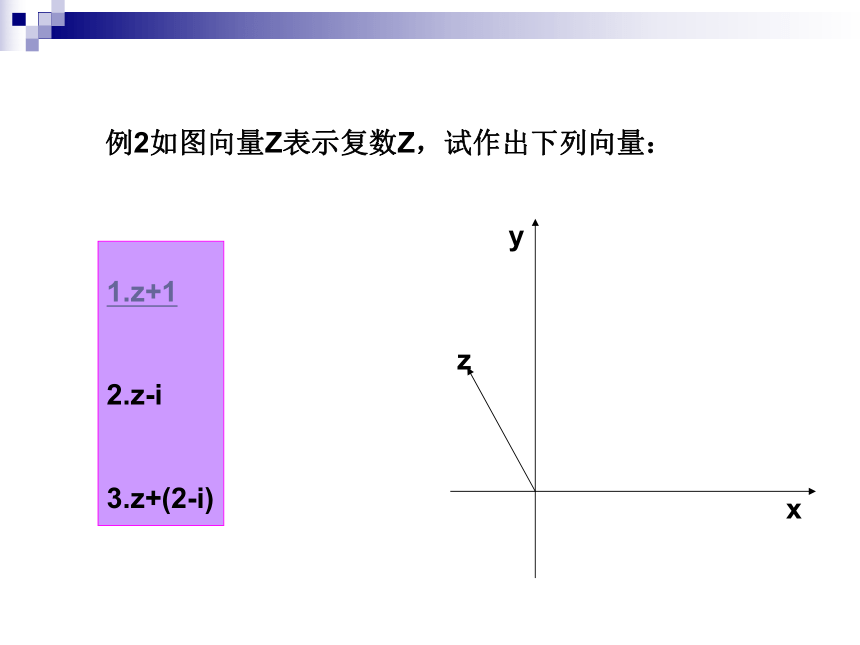
=-11i例2如图向量Z表示复数Z,试作出下列向量:1.z+1
2.z-i
3.z+(2-i)规定2:复数的乘法法则:
因此,两个复数的乘积仍然是一个确定的复数,
它和多项式的运算规则一致复数的乘法是否满足交换律、结合律以及对加法的分配律?我们比较容易证明这些性质:1.交换律:z1·z2=z2·z12.结合律:(z1·z2) ·z3=z1· (z2·z3)3.结合律:z1(z2+z3)=z1z2+z1z3若z=a+bi(a,b∈R),则共轭复数所对应的点关于实轴对称.容易证明有以下特点:(2)实数的除法是其乘法的逆运算,而向量是没有除法运算的,那么复数的除法运算情况怎样的呢?复数的除法法则为:共轭复数有理化小结1.复数加法的代数运算法则及其几何意义2.复数的乘法以及除法的代数运算3.共轭复数
多媒体课件多思、创新、融合复数代数形式的四则运算
及其几何意义前面我们学习了复数的概念及其几何意义:3.相等的向量表示同一个复数。下面我们就来进一步讨论复数的运算性质规定1:复数的加法规则:z1=a+bi,z2=c+di是任意的两个复数,那么
(a+bi)+(c+di)=(a+c)+(b+d)i
因此,两个复数的和仍然是一个确定的复数复数的加法满足交换律和结合律吗?1.加法的代数运算:设,z1,z2,z3∈R,有:z1+z2=z2+z1
(z1+z2)+z3=z1+(z2+z3)(交换律)
(结合律)2加法的几何意义:z1=a+bi,z2=c+di3.减法的运算:如何理解复数的减法?1.代数式:z=a+bi,z1=c+di,且z1+z2=z,则z2=x+yi,z1+z2=z(c+x)(d+y)i=a+bix=a-c
y=b-d2.几何意义:例1.计算(5-6i)+(-2-i)-(3+4i)解 原式=[5+(-2)-(3)]+[(-6)+(-1)-4]i=0+(-11)i
=-11i例2如图向量Z表示复数Z,试作出下列向量:1.z+1
2.z-i
3.z+(2-i)规定2:复数的乘法法则:
因此,两个复数的乘积仍然是一个确定的复数,
它和多项式的运算规则一致复数的乘法是否满足交换律、结合律以及对加法的分配律?我们比较容易证明这些性质:1.交换律:z1·z2=z2·z12.结合律:(z1·z2) ·z3=z1· (z2·z3)3.结合律:z1(z2+z3)=z1z2+z1z3若z=a+bi(a,b∈R),则共轭复数所对应的点关于实轴对称.容易证明有以下特点:(2)实数的除法是其乘法的逆运算,而向量是没有除法运算的,那么复数的除法运算情况怎样的呢?复数的除法法则为:共轭复数有理化小结1.复数加法的代数运算法则及其几何意义2.复数的乘法以及除法的代数运算3.共轭复数
