22.1.4二次函数y=ax?+bx+c的图象和性质强化训练(含答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 22.1.4二次函数y=ax?+bx+c的图象和性质强化训练(含答案) 2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 210.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 13:47:50 | ||
图片预览


文档简介
22.1.4二次函数y=ax +bx+c的图象和性质
一、单选题
1.二次函数y=2x2﹣4x﹣6的最小值是( )
A.﹣8 B.﹣2 C.0 D.6
2.二次函数y=ax2+bx-1(a≠0)的图象经过点(1,-3),则代数式1+a+b的值为( )
A.-3 B.-1 C.2 D.5
3.已知,当且x为整数时,y随x的增大而减小,则m的取值范围是( )
A. B. C. D.
4.在平面直角坐标系中,若移动二次函数y=2(x﹣3)(x﹣4)+6的图象,使其与x轴交于两点,且此两点的距离为1个单位,则移动方式可以为( )
A.向上移动3个单位 B.向下移动3个单位
C.向上移动6个单位 D.向下移动6个单位
5.已知函数(c为常数)的图象上有两点,.若且,则与的大小关系是( )
A. B. C. D.与的大小不确定
6.已知抛物线y=﹣x2+bx﹣c的顶点在直线y=3x+1上,且该抛物线与y轴的交点的纵坐标为n,则n的最大值为( )
A. B. C. D.
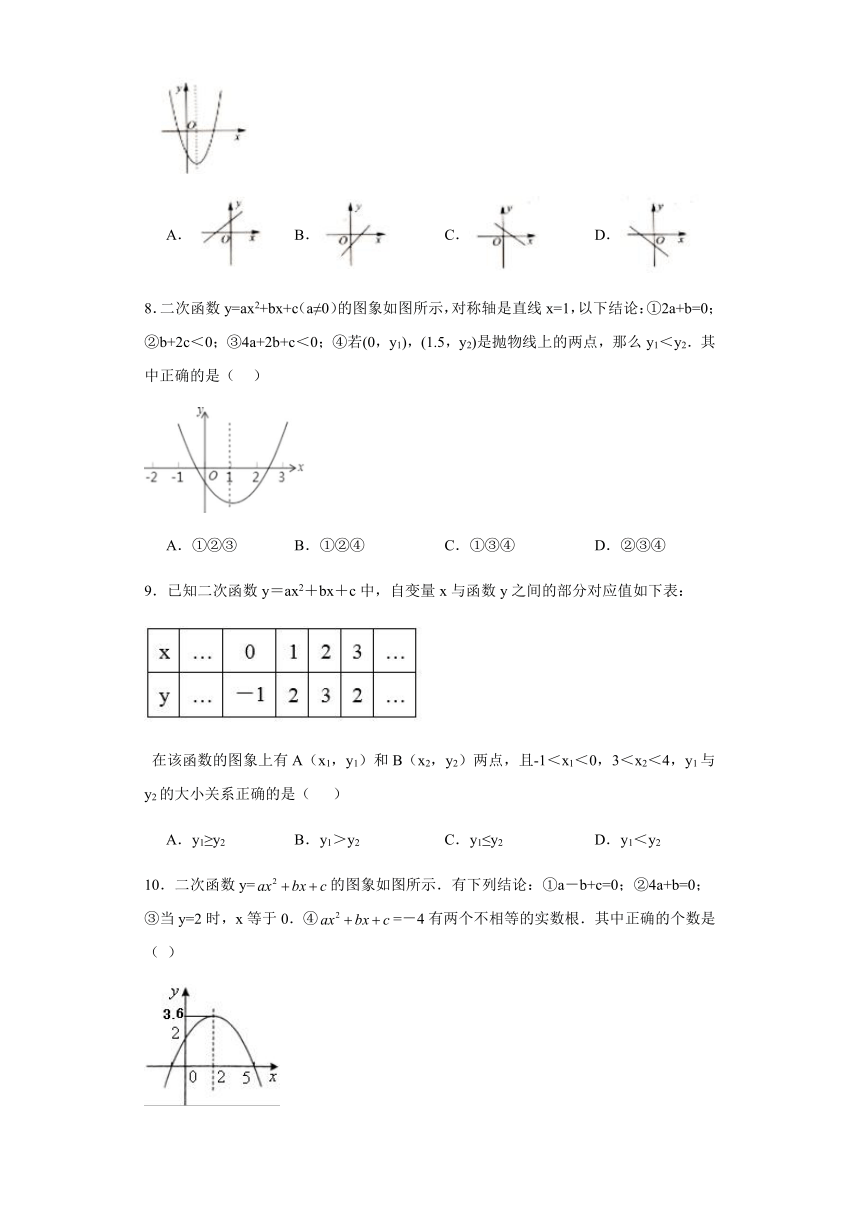
7.在平面直角坐标系中,二次函数的图象如图所示,则一次函数的图象可能是()
A. B. C. D.
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,以下结论:①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),(1.5,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
9.已知二次函数y=ax2+bx+c中,自变量x与函数y之间的部分对应值如下表:
在该函数的图象上有A(x1,y1)和B(x2,y2)两点,且-1<x1<0,3<x2<4,y1与y2的大小关系正确的是( )
A.y1≥y2 B.y1>y2 C.y1≤y2 D.y1<y2
10.二次函数y=的图象如图所示.有下列结论:①a-b+c=0;②4a+b=0;③当y=2时,x等于0.④=-4有两个不相等的实数根.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.把二次函数y= -2x2-4x-1的图象向上平移3个单位长度,再向右平移4个单位长度,则两次平移后的图象的解析式是 ;
12.已知二次函数的函数值y与自变量x的部分对应值如下表:
x … 0 1 2 3 …
y … 8 3 0 0 3 …
则这个二次函数的图象的顶点坐标是 .
13.将抛物线先沿水平方向向右平移1个单位,再沿竖直方向向上平移3个单位,则得到的新抛物线的解析式为 .
14.已知二次函数的对称轴为直线,它的图象顶点坐标为,则 .(用含的代数式表示)
15.已知点和点是抛物线上的两点,则的大小关系是 (填“>”或“<”或“=”).
16.对于二次函数y=﹣x2+2x有下列四个结论:
①它的对称轴是直线x=1;
②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1>0时,有y1>y2;
③它的图象与x轴的两个交点是(0,0)和(2,0);
④直线y=k与y=﹣x2+2x的图象有两个不同的交点,则k<1;
其中正确结论的个数为 .
三、解答题
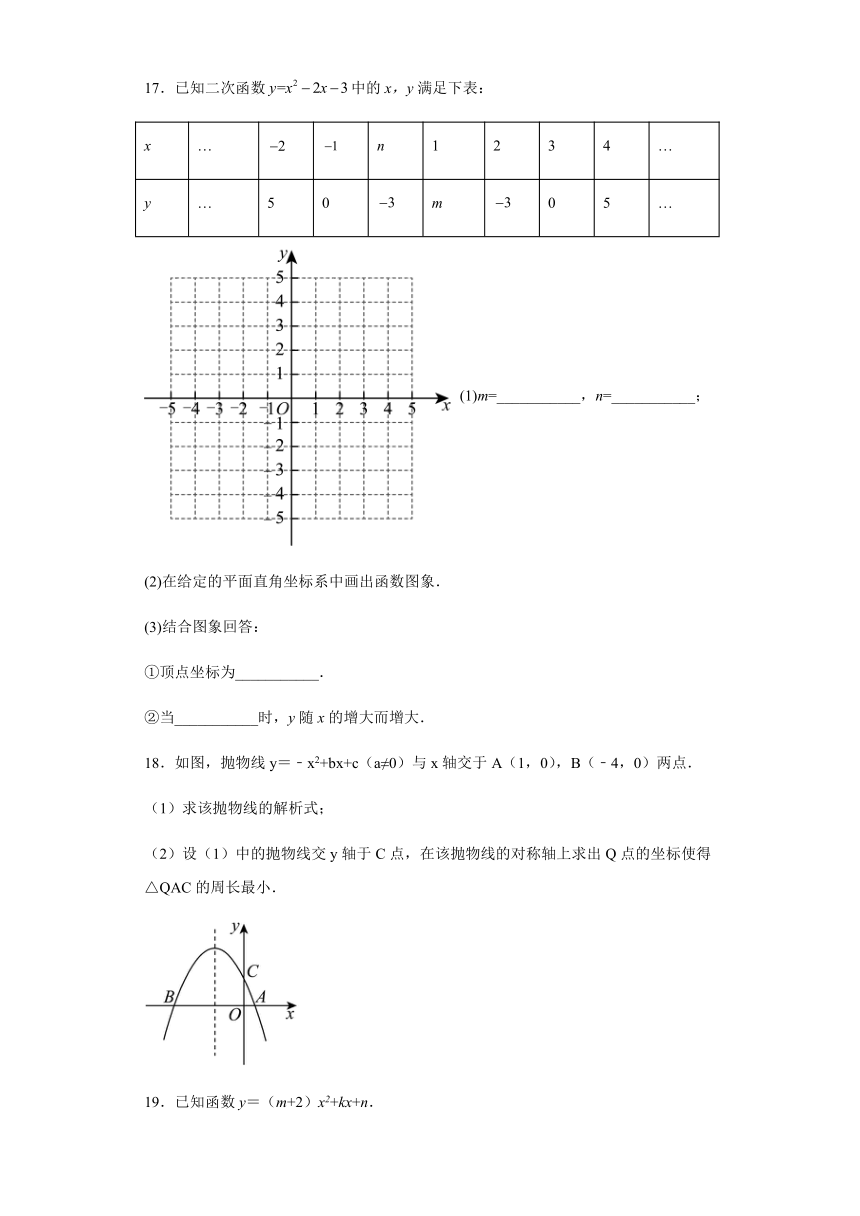
17.已知二次函数中的x,y满足下表:
x … n 1 2 3 4 …
y … 5 0 m 0 5 …
(1)m=___________,n=___________;
(2)在给定的平面直角坐标系中画出函数图象.
(3)结合图象回答:
①顶点坐标为___________.
②当___________时,y随x的增大而增大.
18.如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于A(1,0),B(﹣4,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上求出Q点的坐标使得△QAC的周长最小.
19.已知函数y=(m+2)x2+kx+n.
(1)若此函数为一次函数;
①m,k,n的取值范围;
②当﹣2≤x≤1时,0≤y≤3,求此函数关系式;
③当﹣2≤x≤3时,求此函数的最大值和最小值(用含k,n的代数式表示);
(2)若m=﹣1,n=2,当﹣2≤x≤2时,此函数有最小值﹣4,求实数k的值.
20.如图所示,在平面直角坐标系中,抛物线()经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(,),△PBE的面积为,求与的函数关系式,写出自变量的取值范围.
参考答案:
1.A
2.B
3.D
4.D
5.A
6.A
7.D
8.A
9.D
10.C
11.y= -2x2+12x-14
12.
13.或
14.2-a.
15.=
16.3.
17.,①,②
18.(1)y=﹣x2﹣3x+4(2)Q(﹣,)
19.(1)①m=﹣2,k≠0,n为任意实数;②当k>0时,;当k<0时,;③当k>0时,x=﹣2,y有最小值为﹣2k+n,x=3时,y有最大值为3k+n,当k<0时,x=﹣2,y有最大值为﹣2k+n,x=3时,y有最小值为3k+n;
(2)实数k的值为±5
20.(1),D(1,4);(2)().
一、单选题
1.二次函数y=2x2﹣4x﹣6的最小值是( )
A.﹣8 B.﹣2 C.0 D.6
2.二次函数y=ax2+bx-1(a≠0)的图象经过点(1,-3),则代数式1+a+b的值为( )
A.-3 B.-1 C.2 D.5
3.已知,当且x为整数时,y随x的增大而减小,则m的取值范围是( )
A. B. C. D.
4.在平面直角坐标系中,若移动二次函数y=2(x﹣3)(x﹣4)+6的图象,使其与x轴交于两点,且此两点的距离为1个单位,则移动方式可以为( )
A.向上移动3个单位 B.向下移动3个单位
C.向上移动6个单位 D.向下移动6个单位
5.已知函数(c为常数)的图象上有两点,.若且,则与的大小关系是( )
A. B. C. D.与的大小不确定
6.已知抛物线y=﹣x2+bx﹣c的顶点在直线y=3x+1上,且该抛物线与y轴的交点的纵坐标为n,则n的最大值为( )
A. B. C. D.
7.在平面直角坐标系中,二次函数的图象如图所示,则一次函数的图象可能是()
A. B. C. D.
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,以下结论:①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),(1.5,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
9.已知二次函数y=ax2+bx+c中,自变量x与函数y之间的部分对应值如下表:
在该函数的图象上有A(x1,y1)和B(x2,y2)两点,且-1<x1<0,3<x2<4,y1与y2的大小关系正确的是( )
A.y1≥y2 B.y1>y2 C.y1≤y2 D.y1<y2
10.二次函数y=的图象如图所示.有下列结论:①a-b+c=0;②4a+b=0;③当y=2时,x等于0.④=-4有两个不相等的实数根.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.把二次函数y= -2x2-4x-1的图象向上平移3个单位长度,再向右平移4个单位长度,则两次平移后的图象的解析式是 ;
12.已知二次函数的函数值y与自变量x的部分对应值如下表:
x … 0 1 2 3 …
y … 8 3 0 0 3 …
则这个二次函数的图象的顶点坐标是 .
13.将抛物线先沿水平方向向右平移1个单位,再沿竖直方向向上平移3个单位,则得到的新抛物线的解析式为 .
14.已知二次函数的对称轴为直线,它的图象顶点坐标为,则 .(用含的代数式表示)
15.已知点和点是抛物线上的两点,则的大小关系是 (填“>”或“<”或“=”).
16.对于二次函数y=﹣x2+2x有下列四个结论:
①它的对称轴是直线x=1;
②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1>0时,有y1>y2;
③它的图象与x轴的两个交点是(0,0)和(2,0);
④直线y=k与y=﹣x2+2x的图象有两个不同的交点,则k<1;
其中正确结论的个数为 .
三、解答题
17.已知二次函数中的x,y满足下表:
x … n 1 2 3 4 …
y … 5 0 m 0 5 …
(1)m=___________,n=___________;
(2)在给定的平面直角坐标系中画出函数图象.
(3)结合图象回答:
①顶点坐标为___________.
②当___________时,y随x的增大而增大.
18.如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于A(1,0),B(﹣4,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上求出Q点的坐标使得△QAC的周长最小.
19.已知函数y=(m+2)x2+kx+n.
(1)若此函数为一次函数;
①m,k,n的取值范围;
②当﹣2≤x≤1时,0≤y≤3,求此函数关系式;
③当﹣2≤x≤3时,求此函数的最大值和最小值(用含k,n的代数式表示);
(2)若m=﹣1,n=2,当﹣2≤x≤2时,此函数有最小值﹣4,求实数k的值.
20.如图所示,在平面直角坐标系中,抛物线()经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(,),△PBE的面积为,求与的函数关系式,写出自变量的取值范围.
参考答案:
1.A
2.B
3.D
4.D
5.A
6.A
7.D
8.A
9.D
10.C
11.y= -2x2+12x-14
12.
13.或
14.2-a.
15.=
16.3.
17.,①,②
18.(1)y=﹣x2﹣3x+4(2)Q(﹣,)
19.(1)①m=﹣2,k≠0,n为任意实数;②当k>0时,;当k<0时,;③当k>0时,x=﹣2,y有最小值为﹣2k+n,x=3时,y有最大值为3k+n,当k<0时,x=﹣2,y有最大值为﹣2k+n,x=3时,y有最小值为3k+n;
(2)实数k的值为±5
20.(1),D(1,4);(2)().
同课章节目录
