专题18.16平行四边形折叠和作图问题 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题18.16平行四边形折叠和作图问题 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 659.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 21:45:04 | ||
图片预览


文档简介
专题18.16 平行四边形折叠和作图问题(基础篇)(专项练习)
一、单选题
1.如图,将ABCD沿对角线AC折叠,使点B落在处,若,则为( )
A.66° B.104° C.111° D.124°
2.如图,已知的一组邻边AB,BC,用尺规作图作,下列4个作图中,作法与理论依据都正确的有几个( )
A.1个 B.2个 C.3个 D.4个
3.如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=36°,则∠B为( )
A.127° B.126° C.125° D.124°
4.如图,在□ABCD中,连接AC,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于M、N两点,作直线MN,交AB 于点E,交CD于点F,交AC于点O,连接CE,若AD=6,△BCE的周长为14,则CD的长为( )
A.5 B.6 C.8 D.10
5.如图, ABCD中,点E在边BC上,以AE为折痕,将△ABE向上翻折,点B正好落在CD上的点F处,若△FCE的周长为7,△FDA的周长为21,则FD的长为( )
A.5 B.6 C.7 D.8
6.如图,已知的顶点,点B在x轴正半轴上,按以下步骤作图:①以点D为圆心,适当长度为半径作弧,分别交边于点E,F;②分别以点E,F为圆心,大于的长为半径作弧,两弧在内交于点G;③作射线,交边于点H,则点H的坐标为( )
A. B. C. D.
7.如图,将 ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )
A.AF=EF B.AE=AF C.AB=EF D.FD=EC
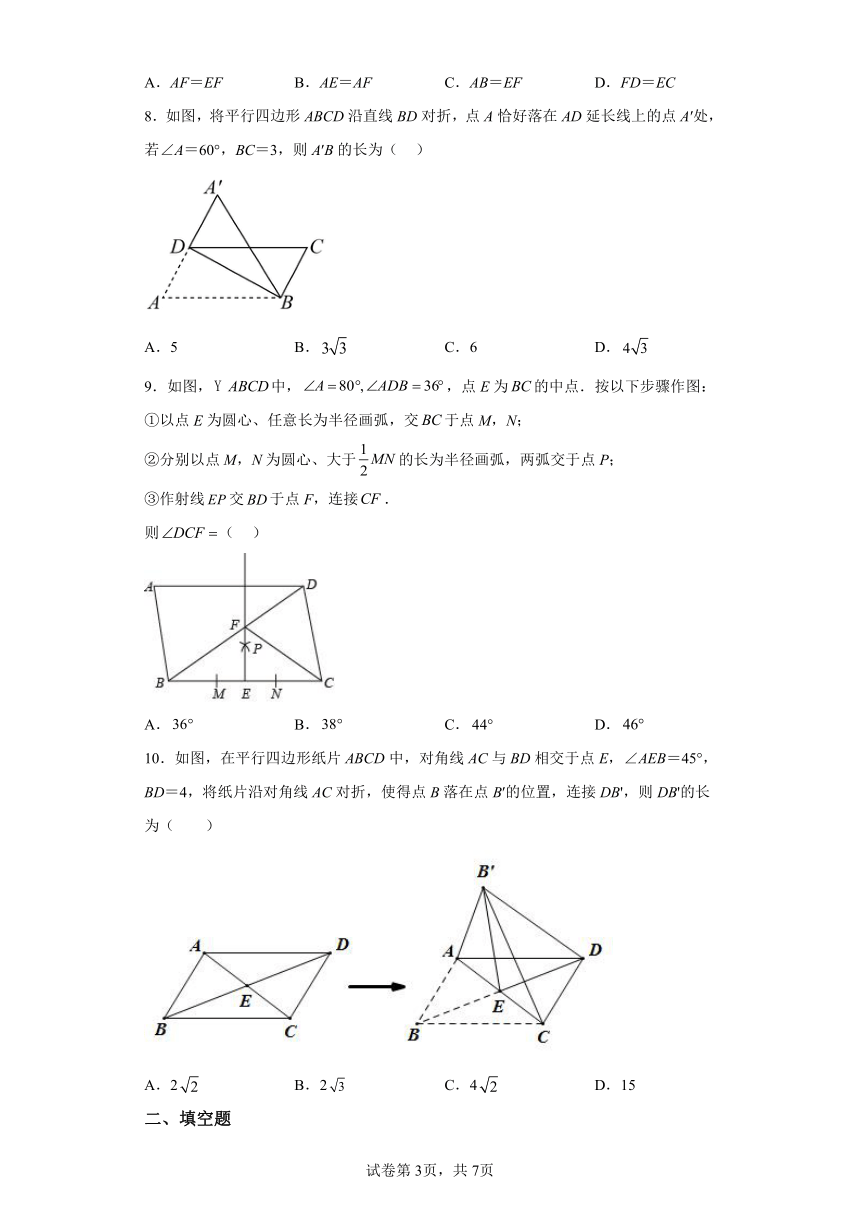
8.如图,将平行四边形ABCD沿直线BD对折,点A恰好落在AD延长线上的点A′处,若∠A=60°,BC=3,则A′B的长为( )
A.5 B. C.6 D.
9.如图,中,,点E为的中点.按以下步骤作图:
①以点E为圆心、任意长为半径画弧,交于点M,N;
②分别以点M,N为圆心、大于的长为半径画弧,两弧交于点P;
③作射线交于点F,连接.
则( )
A. B. C. D.
10.如图,在平行四边形纸片ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=4,将纸片沿对角线AC对折,使得点B落在点B′的位置,连接DB',则DB'的长为( )
A.2 B.2 C.4 D.15
二、填空题
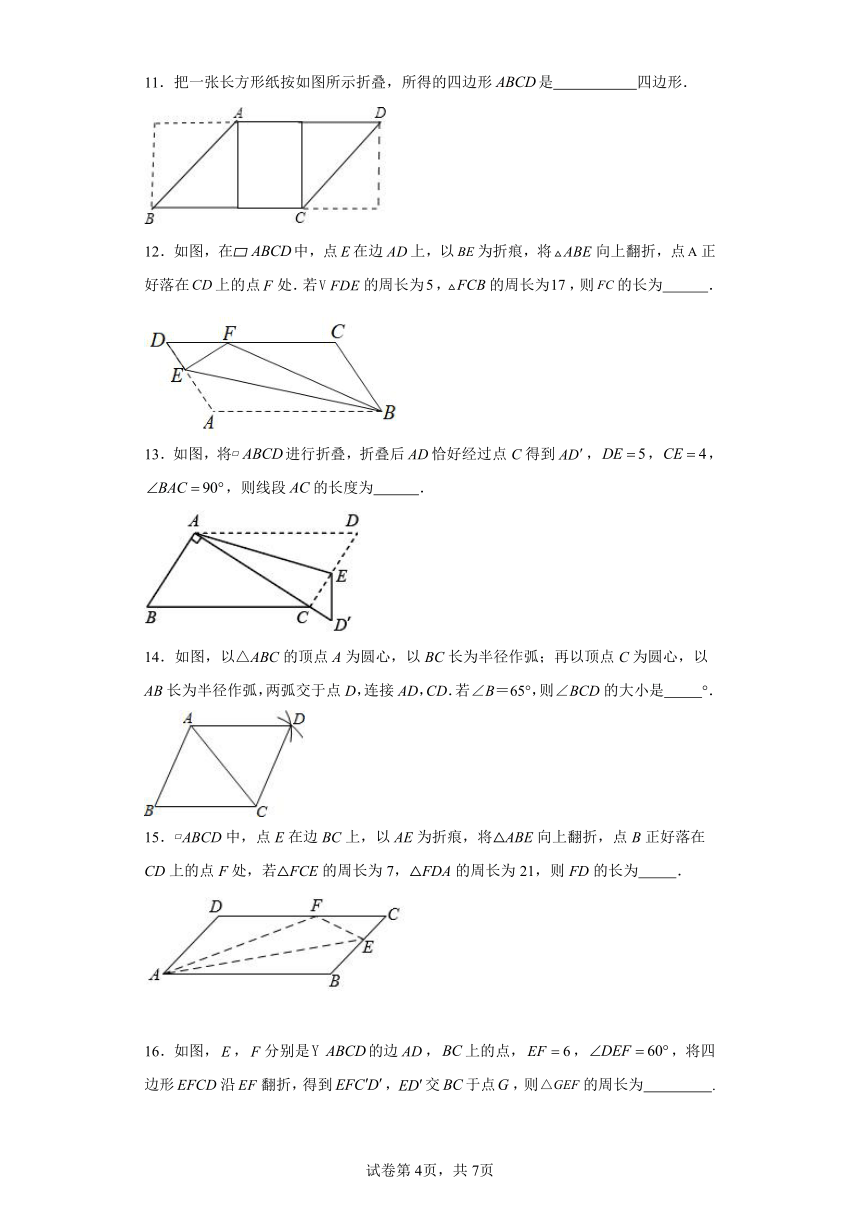
11.把一张长方形纸按如图所示折叠,所得的四边形是 四边形.
12.如图,在 中,点在边上,以为折痕,将向上翻折,点正好落在上的点处.若的周长为,的周长为,则的长为 .
13.如图,将 进行折叠,折叠后恰好经过点C得到,,,,则线段的长度为 .
14.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠BCD的大小是 °.
15. ABCD中,点E在边BC上,以AE为折痕,将△ABE向上翻折,点B正好落在CD上的点F处,若△FCE的周长为7,△FDA的周长为21,则FD的长为 .
16.如图,,分别是的边,上的点,,,将四边形沿翻折,得到,交于点,则的周长为 .
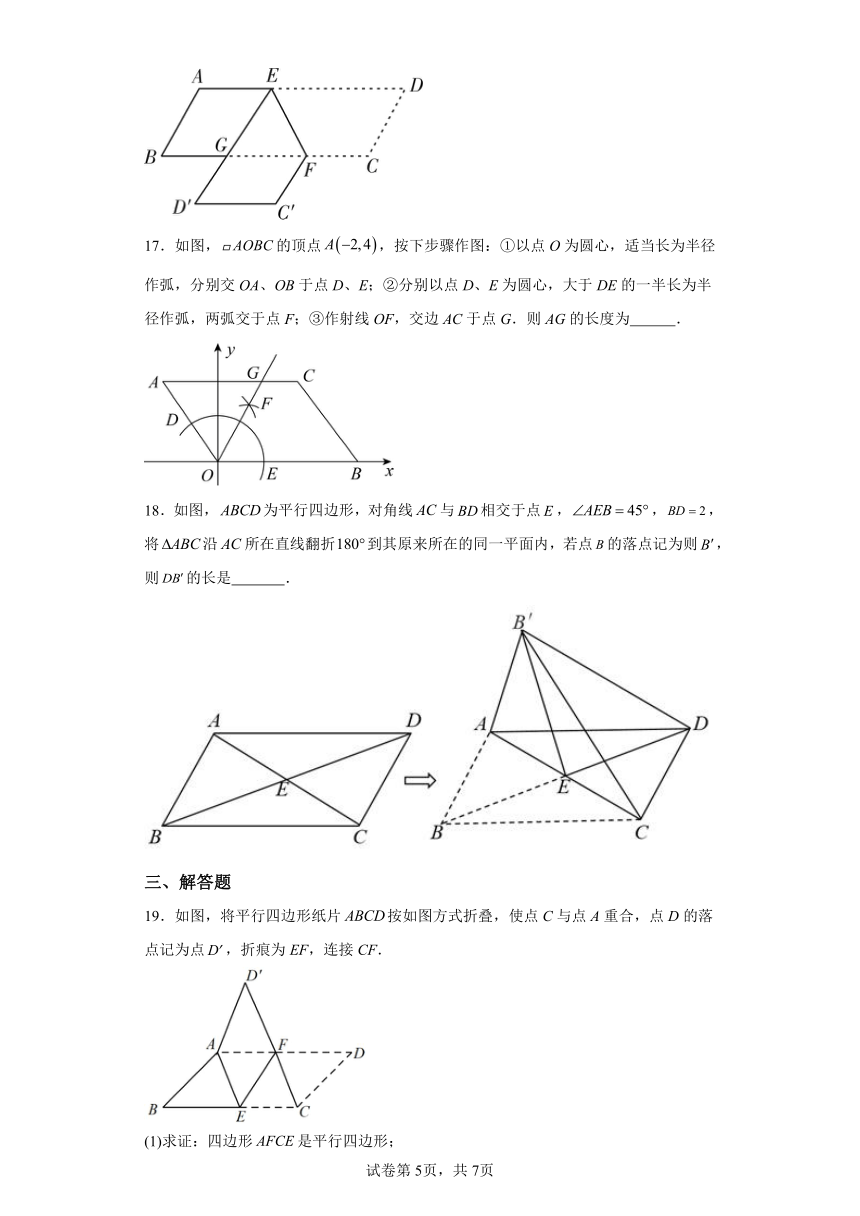
17.如图,的顶点,按下步骤作图:①以点O为圆心,适当长为半径作弧,分别交OA、OB于点D、E;②分别以点D、E为圆心,大于DE的一半长为半径作弧,两弧交于点F;③作射线OF,交边AC于点G.则AG的长度为 .
18.如图,为平行四边形,对角线与相交于点,,,将沿所在直线翻折到其原来所在的同一平面内,若点的落点记为则,则的长是 .
三、解答题
19.如图,将平行四边形纸片按如图方式折叠,使点C与点A重合,点D的落点记为点,折痕为EF,连接CF.
(1)求证:四边形是平行四边形;
(2)若,求线段的长.
20.将一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E,F均在BD上),折痕分别为DH,BG.
(1)求证:四边形BGDH为平行四边形;
(2)若AB=6,BC=8,求四边形BGDH的周长.
21.如图,将平行四边形ABCD沿着对角线BD折叠,点C的对应点为C′,BC′与AD相交于点E.
(1) EB与ED相等吗?证明你的结论;
(2)连接AC′,判断AC′与BD的位置关系,并说明理由.
22.如图,将□ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
(1)求证:四边形ABFE为平行四边形;
(2)若,求四边形ABFE的周长.
23.如图,将ABCD沿过点A的直线折叠,使点D落到AB边上的点处,折痕交CD边于点E,连接BE
(1)求证:四边形是平行四边形
(2)若BE平分∠ABC,求证:
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】由平行四边形的性质和折叠的性质得出∠ACD=∠BAC=∠B′AC,由三角形的外角性质求出∠BAC=∠ACD=∠B′AC=∠1,再由三角形内角和定理求出∠B即可.
【详解】解:∵四边形ABCD是平行四边形,
∴ABCD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=∠1=23°,
∴∠B=180°-∠2-∠BAC=180°-46°-23°=111°,
故选:C.
【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质,求出∠BAC的度数是解决问题的关键.
2.C
【分析】根据各个图形的做法结合平行四边形的判定方法进行判断即可.
【详解】解:图①,由作图可知,根据“两组对边分别相等的四边形是平行四边形”可知,图①作法与理论依据正确;
图②,
由作图可知,作AC的垂直平分线,得到AC的中点O,再连接BO并延长到点D,使,根据“对角线互相平分的四边形是平行四边形”可得,图2作法与理论依据正确;
图③,作同位角相等,得出,再截取,根据“一组对边平行且相等的四边形是平行四边形”可得,图3作法与理论依据正确;
图④,作同位角相等,得出,再截取,“一组对边平行,另一组对边相等的四边形不一定是平行四边形”,因此图4作法与理论依据不正确;
综上所述,作法与理论依据正确的是图①、图②、图③,共3个.
故选:C.
【点睛】本题考查尺规作图,平行四边形的判定,掌握平行四边形的判定方法及尺规作图的意义是解题的关键.
3.B
【分析】根据翻折可得∠B′AC=∠BAC,根据平行四边形可得DC∥AB,所以∠BAC=∠DCA,从而可得∠1=2∠BAC,进而求解.
【详解】解:根据翻折可知:∠B′AC=∠BAC,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠BAC=∠DCA,
∴∠BAC=∠DCA=∠B′AC,
∵∠1=∠B′AC+∠DCA,
∴∠1=2∠BAC=36°,
∴∠BAC=18°,
∴∠B=180°-∠BAC-∠2=180°-18°-36°=126°,
故选:B.
【点睛】本题考查了翻折变换、平行四边形的性质,解决本题的关键是利用翻折的性质.
4.C
【分析】根据平行四边形的性质可知AD=BC=6,CD=AB,再由垂直平分线的性质得出AE=CE,据此可得出结论.
【详解】解:∵由作图可知,MN是线段AC的垂直平分线,
∴AE=CE,
∵四边形ABCD是平行四边形,AD=6,
∴AD=BC=6,CD=AB,
∵△BCE的周长为14,
∴BE+EC+BC= BE+AE+BC=AB+BC=6+AB=14,
则CD=AB=8.
故选:C.
【点睛】本题考查的是作图-基本作图,熟知线段垂直平分线的作法是解答此题的关键.
5.C
【分析】根据翻折变换的性质、平行四边形的性质证明AD+DC=14,此为解题的关键性结论;再运用△FDA的周长为21,求出FD的长,即可解决问题.
【详解】解:∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC.
由题意得,BE=FE,AB=AF.
∵△FCE的周长为7,△FDA的周长为21,
∴CE+CF+EF=7,DF+AD+AF=21,
∴(CE+EF)+(DF+CF)+AD+AF=28,
即2(AD+DC)=28,
∴AD+DC=14,即AD+AF=14,
∴FD=21-14=7.
故选:C.
【点睛】本题考查了翻折变换的性质及平行四边形的性质,根据以上性质找到等量关系AD+DC=14是解题的关键.
6.A
【分析】依据勾股定理即可得到Rt△AOD中,AD=,依据∠AHD=∠ADH,即可得到AH=AD=,可得H(,2).
【详解】∵的顶点,
∴AO=2,OD=1,
∴Rt△ADD中,AD=,
由题可得,DG平分∠ADB,
∴∠ADH=∠FDH,
又∵AH∥DF,
∴∠AHD=∠FDH,
∴∠AHD=∠ADH,
∴AH=AD=,
∴H(,2),
故选A.
【点睛】本题主要考查了角平分线的作法,勾股定理以及平行四边形的性质的运用,解题时注意:求图形中一些点的坐标时,过已知点向坐标轴作垂线,然后求出相关的线段长,是解题的关键.
7.B
【分析】根据平行四边形的性质及折叠变换进行推理,可知A、C、D均成立,只有B不成立.
【详解】解:∵平行四边形ABCD沿AE翻折,
∴△ABE≌△AFE,
∴AB=AF,BE=EF,∠AEB=∠AEF,
∵AD∥BC,
∴∠AEB=∠EAF,
∴∠AEF=∠EAF,
∴AF=EF,故选项A正确,不符合题意;
∴AF=BE
∴四边形ABEF为平行四边形,
∴AB=EF=AF=BE,故选项C正确,不符合题意,
∵AD=BC,
∴AD AF=BC BE,即FD=EC,故选项D正确,不符合题意;
不能证明选项B,故选项B不一定成立,符合题意;
故选:B.
【点睛】本题考查平行四边形中的翻折问题,已知翻折就是图形全等,翻折是一种对称变换,它属于轴对称,解题的关键是掌握轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
8.C
【分析】由折叠可得.,,,根据和三角形内角和定理得,根据平行四边形的性质得,根据直角三角形的性质即可得.
【详解】解:由折叠可得,,,,
∵,
∴,
∵四边形ABCD是平行四边形,,
∴,
∴,
故选C.
【点睛】本题考查了折叠的性质,平行四边形的性质,直角三角形的性质,解题的关键是掌握这些知识点.
9.C
【分析】根据三角形内角和求出,由平行四边形的性质,求出,由题意得垂直平分,利用垂直平分线的性质求解.
【详解】解:根据三角形内角和,
,
,
由题意得:垂直平分,
∴FB=FC,
,
而,
则,
故选:C.
【点睛】本题考查了三角形内角和定理、垂直平分线的性质、平行四边形的性质,解题的关键是掌握垂直平分线的性质.
10.A
【分析】先利用平行四边形的性质得到,再由折叠的性质得到,,由此可得到,再利用勾股定理求解即可.
【详解】解:∵四边形ABCD是平行四边形,
∴,
由折叠的性质可知:,,
∴,
∴,
∴在直角三角形中,
故选A.
【点睛】本题主要考查了平行四边形的性质,折叠的性质,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
11.平行
【分析】长方形对边平行,有;由折叠知根据“有一组对边平行,一组对角相等的四边形是平行四边形”作出判断.
【详解】解:纸片为长方形,
∴.
∴,
由叠法知,
.
∴,
∴,
是平行四边形.
故答案为:平行.
【点睛】此题考查了平行四边形的判断,折叠的性质,关键是掌握两组对边分别平行的四边形是平行四边形.
12.6
【分析】根据翻折变换的性质、平行四边形的性质证明,此为解题的关键性结论;运用的周长为,求出的长,即可解决问题.
【详解】解:如图,四边形为平行四边形,
,;
由题意得:,;
的周长为,的周长为,
,,
,
即,
,即;
,
故答案为:.
【点睛】该题主要考查了翻折变换的性质、平行四边形的性质等几何知识点及其应用问题,解题的方法是准确找出图形中隐含的等量关系;解题的关键是灵活运用翻折变换的性质、平行四边形的性质等几何知识点来分析、判断、解答.
13.
【分析】由平行四边形的性质可得AD=BC,AB=CD=DE+CE=9,ABCD,可得∠=90°,由折叠的性质可得=DE=5,AD=,由勾股定理可求的长,AC的长.
【详解】解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD=DE+CE=9,ABCD,
∴∠BAC=∠ACD=90°,
∴∠=90°,
∵将平行四边形ABCD进行折叠,折叠后AD恰好经过点C得到,
∴=DE=5,AD=,
∴= =3,
∴=AC+3=AD=BC,
∵,
∴,
∴AC=12,
故答案为:12.
【点睛】本题考查了翻折变换,平行四边形的性质,求出的长是本题的关键.
14.115
【分析】根据以为圆心,以长为半径作弧;再以顶点为圆心,以长为半径作弧,得,,得四边形是平行四边形,根据平行四边形的性质,即可求出.
【详解】∵以为圆心,以长为半径作弧;再以顶点为圆心,以长为半径作弧
∴,
∴四边形是平行四边形
∴
∴
∵
∴
故答案为:.
【点睛】本题考查平行四边形的知识,解题的关键是熟练掌握平行四边形的判定和性质.
15.7
【分析】根据翻折变换的性质、平行四边形的性质证明AD+DC=14,此为解题的关键性结论;运用△FDA的周长为21,求出FD的长,即可解决问题.
【详解】解:∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC;
由题意得:BE=FE,AB=AF;
∵△FCE的周长为7,△FDA的周长为21,
∴CE+CF+EF=7,DF+AD+AF=21,
∴(CE+EF)+(DF+CF)+AD+AF=28,
即2(AD+DC)=28,
∴AD+DC=14,即AD+AF=14,
∴FD=21-14=7,
故答案为:7.
【点睛】本题考查了翻折变换的性质、平行四边形的性质等几何知识点及其应用问题,解题的方法是准确找出图形中隐含的等量关系;解题的关键是灵活运用翻折变换的性质、平行四边形的性质等几何知识点来分析、判断、解答.
16.18
【分析】根据平行四边形的性质得到AD∥BC,由平行线的性质得到∠AEG=∠EGF,根据折叠的性质得到∠GEF=,推出△EGF是等边三角形,于是得到结论.
【详解】解:∵四辺形ABCD是平行四辺形,
∴AD∥BC,
∴∠AEG=∠EGF,
∵将四边形沿翻折,得到,
∴∠GEF=,
∴∠AEG=60°,
∴∠EGF=60°,
∴△EGF是等边三角形,
∵EF=6,
∴△GEF的周长=18.
故答案为:18.
【点睛】此题考查平行四边形的性质,折叠的性质,等边三角形的判定及性质,熟练掌握运用这些知识点是解题关键.
17.
【分析】如图,先利用勾股定理计算出OA=,再利用基本作图和平行线的性质得到∠AOG=∠AGO,则AG=AO=,从而求解.
【详解】解:如图,∵ AOBC的顶点A的坐标为,
∴ACOB,OA=,
由作法得OG平分∠AOB,
∴∠AOG=∠BOG,
而ACOB,
∴∠AGO=∠BOG,
∴∠AOG=∠AGO,
∴AG=AO=,
故答案为:.
【点睛】本题考查了作图 基本作图,解题的关键是熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了平行四边形的性质.
18.
【分析】利用折叠的性质和平行四边形的性质得到△B′ED是等腰直角三角形,由等腰直角三角形的性质解答即可.
【详解】解:根据折叠的性质知,∠BEA=∠B′EA=45°,则∠B′ED=90°.
又由折叠的性质得BE=B′E
∵平行四边形ABCD
∴BE=DE,
∴BE=DE=B′E,
∴△B′ED是等腰直角三角形,
∴DB′=DE=×BD=.
故答案为:.
【点睛】本题考查了平行四边形的性质,等腰三角形的判定与性质以及翻折变换(折叠的性质).推知DB′=BB′是解题的关键.
19.(1)见解析
(2)
【分析】(1)先证明四边形AFCE是平行四边形,再运用有一组邻边相等的平行四边形是菱形来进行证明;
(2)作AG⊥BE于点G,因为D′F=DF,再证明DF=BE,用勾股定理分别计算BG、EB即可.
【详解】(1)解:证明:∵点C与点A重合,折痕为EF,
∴∠AEF=∠CEF,AE=EC,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF,
∴AF=EC,
又∵AF∥EC,
∴四边形AFCE是平行四边形,
又∵AE=AF,
∴四边形AFCE为菱形.
(2)如图,作AG⊥BE于点G,
则∠AGB=∠AGE=90°,
∵点D的落点为点D′,折痕为EF,
∴D'F=DF.
∵四边形ABCD为平行四边形,
∴AD=BC.
又∵AF=EC,
∴AD-AF=BC-EC,即DF=BE.
∵在Rt△AGB中,∠AGB=90°,∠B=45°,AB=,
∴AG=GB=6.
∵四边形AFCE为平行四边形,
∴AE∥FC.
∴∠AEB=∠FCE=60°.
∵在Rt△AGE中,∠AGE=90°,∠4=60°,
∴GE==,
∴BE=BG+GE=,
∴D′F=.
【点睛】本题主要考查了折叠的性质、菱形的性质与判定、勾股定理的综合运用,运用折叠的性质和平行四边形的性质发现D′F=BE是解题的关键.
20.(1)见解析
(2)10+6.
【分析】(1)由折叠的性质及平行线的性质证得BH∥DG,AD∥BC,则结论得证;
(2)设CG=x,则FG=x,BG=8-x,由勾股定理得出(8-x)2=42+x2.解方程可求得x的值,进一步计算即可求解.
【详解】(1)证明:如图,
∵四边形ABCD为矩形,
∴AB∥CD,AD∥BC,
∴∠ABD=∠CDB,
又由折叠可得:∠1=∠2,∠3=∠4,
∴∠2=∠ABD=∠CDB=∠3,
∴BH∥DG,
∵AD∥BC,
∴四边形BGDH为平行四边形;
(2)解:由折叠可得FG=CG,DF=DC=6,∠DFG=∠C=90°,
在Rt△BCD中,
∵BD2=BC2+CD2,
∴BD==10,
∴BF=10-6=4,
设CG=x,则FG=x,BG=8-x,
在Rt△BGF中,
∵BF2+FG2=BG2,42+x2=(8-x)2,
解得:x=3,
即FG=CG=3.
∴BG=8-3=5,DG==3,
∴四边形BGDH的周长为2(BG+DG)=10+6.
【点睛】本题是四边形综合题,考查了折叠的性质,平行线的性质,矩形的性质,勾股定理等知识,熟练掌握折叠的性质是解题的关键.
21.(1)EB与ED相等,证明过程见解析
(2)AC′∥BD.理由见解析
【分析】(1)依据平行线的性质以及折叠的性质,即可得到∠EDB=∠CBD,进而得出BE=DE;
(2)由BE=DE,进而得出AE=CE,再根据三角形内角和定理,即可得到∠EAC'=∠EC'A=∠EBD=∠EDB,进而得出AC'∥BD.
【详解】(1)解:EB与ED相等.
由折叠可得,∠CBD=∠C'BD,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE;
(2)解:AC′∥BD.理由如下:
∵四边形ABCD平行四边形,
∴AD=BC,
由折叠知,BC'=BC,
∴AD=BC',
由(1)知BE=DE,
∴AE=C'E,
∴∠DAC'=(180°-∠AEC')=90°-∠AEC',
同理:∠ADB=90°-∠BED,
∵∠AEC'=∠BED,
∴∠DAC'=∠ADB,
∴AC'∥BD,
故答案为:AC′∥BD.
【点睛】本题主要考查了折叠问题以及平行四边形的性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
22.(1)见解析;(2)12.
【分析】(1)根据折叠的性质得到∠CFE=∠CDE,根据平行四边形的性质得到AD∥BC,∠B=∠D,由平行线的判定得到AE∥BF,即可得到结论;
(2)根据折叠的性质得到ED=EF,则AE+AB=AE+ED=AD,从而求出四边形ABFE的周长.
【详解】(1)证明:
∵将 □ABCD沿CE折叠,使点D落在BC边上的F处,
∴∠CFE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴AE∥BF,∠B=∠CFE,
∴AB∥EF,
∴四边形ABFE为平行四边形;
(2)∵将 □ABCD沿CE折叠,使点D落在BC边上的F处,
∴DE=EF,
∵四边形ABFE为平行四边形,
∴EF=AB=ED,
∵BC=6,
∴AD=6,
∴AE+AB=AE+ED=AD=6,
∴四边形ABFE的周长=AB+BF+EF+EA=12,
故四边形ABFE的周长为:12.
【点睛】本题考查了平行四边形的判定和性质,折叠的性质,熟练掌握全等三角形及平行四边形知识是解题的关键.
23.见解析
【分析】试题分析:(1)根据翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,然后根据平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形;
(2)根据平行线的性质利用勾股定理得出答案.
【详解】(1)∵将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴ABDC,ABDC
∴CED′B,CED′B,
∴四边形BCED′是平行四边形;
(2)∵BE平分∠ABC,
∴∠CBE=∠EBA,
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AB2=AE2+BE2.
【点睛】考点:1.平行四边形的判定与性质2.勾股定理
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,将ABCD沿对角线AC折叠,使点B落在处,若,则为( )
A.66° B.104° C.111° D.124°
2.如图,已知的一组邻边AB,BC,用尺规作图作,下列4个作图中,作法与理论依据都正确的有几个( )
A.1个 B.2个 C.3个 D.4个
3.如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=36°,则∠B为( )
A.127° B.126° C.125° D.124°
4.如图,在□ABCD中,连接AC,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于M、N两点,作直线MN,交AB 于点E,交CD于点F,交AC于点O,连接CE,若AD=6,△BCE的周长为14,则CD的长为( )
A.5 B.6 C.8 D.10
5.如图, ABCD中,点E在边BC上,以AE为折痕,将△ABE向上翻折,点B正好落在CD上的点F处,若△FCE的周长为7,△FDA的周长为21,则FD的长为( )
A.5 B.6 C.7 D.8
6.如图,已知的顶点,点B在x轴正半轴上,按以下步骤作图:①以点D为圆心,适当长度为半径作弧,分别交边于点E,F;②分别以点E,F为圆心,大于的长为半径作弧,两弧在内交于点G;③作射线,交边于点H,则点H的坐标为( )
A. B. C. D.
7.如图,将 ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )
A.AF=EF B.AE=AF C.AB=EF D.FD=EC
8.如图,将平行四边形ABCD沿直线BD对折,点A恰好落在AD延长线上的点A′处,若∠A=60°,BC=3,则A′B的长为( )
A.5 B. C.6 D.
9.如图,中,,点E为的中点.按以下步骤作图:
①以点E为圆心、任意长为半径画弧,交于点M,N;
②分别以点M,N为圆心、大于的长为半径画弧,两弧交于点P;
③作射线交于点F,连接.
则( )
A. B. C. D.
10.如图,在平行四边形纸片ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=4,将纸片沿对角线AC对折,使得点B落在点B′的位置,连接DB',则DB'的长为( )
A.2 B.2 C.4 D.15
二、填空题
11.把一张长方形纸按如图所示折叠,所得的四边形是 四边形.
12.如图,在 中,点在边上,以为折痕,将向上翻折,点正好落在上的点处.若的周长为,的周长为,则的长为 .
13.如图,将 进行折叠,折叠后恰好经过点C得到,,,,则线段的长度为 .
14.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD,CD.若∠B=65°,则∠BCD的大小是 °.
15. ABCD中,点E在边BC上,以AE为折痕,将△ABE向上翻折,点B正好落在CD上的点F处,若△FCE的周长为7,△FDA的周长为21,则FD的长为 .
16.如图,,分别是的边,上的点,,,将四边形沿翻折,得到,交于点,则的周长为 .
17.如图,的顶点,按下步骤作图:①以点O为圆心,适当长为半径作弧,分别交OA、OB于点D、E;②分别以点D、E为圆心,大于DE的一半长为半径作弧,两弧交于点F;③作射线OF,交边AC于点G.则AG的长度为 .
18.如图,为平行四边形,对角线与相交于点,,,将沿所在直线翻折到其原来所在的同一平面内,若点的落点记为则,则的长是 .
三、解答题
19.如图,将平行四边形纸片按如图方式折叠,使点C与点A重合,点D的落点记为点,折痕为EF,连接CF.
(1)求证:四边形是平行四边形;
(2)若,求线段的长.
20.将一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E,F均在BD上),折痕分别为DH,BG.
(1)求证:四边形BGDH为平行四边形;
(2)若AB=6,BC=8,求四边形BGDH的周长.
21.如图,将平行四边形ABCD沿着对角线BD折叠,点C的对应点为C′,BC′与AD相交于点E.
(1) EB与ED相等吗?证明你的结论;
(2)连接AC′,判断AC′与BD的位置关系,并说明理由.
22.如图,将□ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
(1)求证:四边形ABFE为平行四边形;
(2)若,求四边形ABFE的周长.
23.如图,将ABCD沿过点A的直线折叠,使点D落到AB边上的点处,折痕交CD边于点E,连接BE
(1)求证:四边形是平行四边形
(2)若BE平分∠ABC,求证:
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】由平行四边形的性质和折叠的性质得出∠ACD=∠BAC=∠B′AC,由三角形的外角性质求出∠BAC=∠ACD=∠B′AC=∠1,再由三角形内角和定理求出∠B即可.
【详解】解:∵四边形ABCD是平行四边形,
∴ABCD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=∠1=23°,
∴∠B=180°-∠2-∠BAC=180°-46°-23°=111°,
故选:C.
【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质,求出∠BAC的度数是解决问题的关键.
2.C
【分析】根据各个图形的做法结合平行四边形的判定方法进行判断即可.
【详解】解:图①,由作图可知,根据“两组对边分别相等的四边形是平行四边形”可知,图①作法与理论依据正确;
图②,
由作图可知,作AC的垂直平分线,得到AC的中点O,再连接BO并延长到点D,使,根据“对角线互相平分的四边形是平行四边形”可得,图2作法与理论依据正确;
图③,作同位角相等,得出,再截取,根据“一组对边平行且相等的四边形是平行四边形”可得,图3作法与理论依据正确;
图④,作同位角相等,得出,再截取,“一组对边平行,另一组对边相等的四边形不一定是平行四边形”,因此图4作法与理论依据不正确;
综上所述,作法与理论依据正确的是图①、图②、图③,共3个.
故选:C.
【点睛】本题考查尺规作图,平行四边形的判定,掌握平行四边形的判定方法及尺规作图的意义是解题的关键.
3.B
【分析】根据翻折可得∠B′AC=∠BAC,根据平行四边形可得DC∥AB,所以∠BAC=∠DCA,从而可得∠1=2∠BAC,进而求解.
【详解】解:根据翻折可知:∠B′AC=∠BAC,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠BAC=∠DCA,
∴∠BAC=∠DCA=∠B′AC,
∵∠1=∠B′AC+∠DCA,
∴∠1=2∠BAC=36°,
∴∠BAC=18°,
∴∠B=180°-∠BAC-∠2=180°-18°-36°=126°,
故选:B.
【点睛】本题考查了翻折变换、平行四边形的性质,解决本题的关键是利用翻折的性质.
4.C
【分析】根据平行四边形的性质可知AD=BC=6,CD=AB,再由垂直平分线的性质得出AE=CE,据此可得出结论.
【详解】解:∵由作图可知,MN是线段AC的垂直平分线,
∴AE=CE,
∵四边形ABCD是平行四边形,AD=6,
∴AD=BC=6,CD=AB,
∵△BCE的周长为14,
∴BE+EC+BC= BE+AE+BC=AB+BC=6+AB=14,
则CD=AB=8.
故选:C.
【点睛】本题考查的是作图-基本作图,熟知线段垂直平分线的作法是解答此题的关键.
5.C
【分析】根据翻折变换的性质、平行四边形的性质证明AD+DC=14,此为解题的关键性结论;再运用△FDA的周长为21,求出FD的长,即可解决问题.
【详解】解:∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC.
由题意得,BE=FE,AB=AF.
∵△FCE的周长为7,△FDA的周长为21,
∴CE+CF+EF=7,DF+AD+AF=21,
∴(CE+EF)+(DF+CF)+AD+AF=28,
即2(AD+DC)=28,
∴AD+DC=14,即AD+AF=14,
∴FD=21-14=7.
故选:C.
【点睛】本题考查了翻折变换的性质及平行四边形的性质,根据以上性质找到等量关系AD+DC=14是解题的关键.
6.A
【分析】依据勾股定理即可得到Rt△AOD中,AD=,依据∠AHD=∠ADH,即可得到AH=AD=,可得H(,2).
【详解】∵的顶点,
∴AO=2,OD=1,
∴Rt△ADD中,AD=,
由题可得,DG平分∠ADB,
∴∠ADH=∠FDH,
又∵AH∥DF,
∴∠AHD=∠FDH,
∴∠AHD=∠ADH,
∴AH=AD=,
∴H(,2),
故选A.
【点睛】本题主要考查了角平分线的作法,勾股定理以及平行四边形的性质的运用,解题时注意:求图形中一些点的坐标时,过已知点向坐标轴作垂线,然后求出相关的线段长,是解题的关键.
7.B
【分析】根据平行四边形的性质及折叠变换进行推理,可知A、C、D均成立,只有B不成立.
【详解】解:∵平行四边形ABCD沿AE翻折,
∴△ABE≌△AFE,
∴AB=AF,BE=EF,∠AEB=∠AEF,
∵AD∥BC,
∴∠AEB=∠EAF,
∴∠AEF=∠EAF,
∴AF=EF,故选项A正确,不符合题意;
∴AF=BE
∴四边形ABEF为平行四边形,
∴AB=EF=AF=BE,故选项C正确,不符合题意,
∵AD=BC,
∴AD AF=BC BE,即FD=EC,故选项D正确,不符合题意;
不能证明选项B,故选项B不一定成立,符合题意;
故选:B.
【点睛】本题考查平行四边形中的翻折问题,已知翻折就是图形全等,翻折是一种对称变换,它属于轴对称,解题的关键是掌握轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
8.C
【分析】由折叠可得.,,,根据和三角形内角和定理得,根据平行四边形的性质得,根据直角三角形的性质即可得.
【详解】解:由折叠可得,,,,
∵,
∴,
∵四边形ABCD是平行四边形,,
∴,
∴,
故选C.
【点睛】本题考查了折叠的性质,平行四边形的性质,直角三角形的性质,解题的关键是掌握这些知识点.
9.C
【分析】根据三角形内角和求出,由平行四边形的性质,求出,由题意得垂直平分,利用垂直平分线的性质求解.
【详解】解:根据三角形内角和,
,
,
由题意得:垂直平分,
∴FB=FC,
,
而,
则,
故选:C.
【点睛】本题考查了三角形内角和定理、垂直平分线的性质、平行四边形的性质,解题的关键是掌握垂直平分线的性质.
10.A
【分析】先利用平行四边形的性质得到,再由折叠的性质得到,,由此可得到,再利用勾股定理求解即可.
【详解】解:∵四边形ABCD是平行四边形,
∴,
由折叠的性质可知:,,
∴,
∴,
∴在直角三角形中,
故选A.
【点睛】本题主要考查了平行四边形的性质,折叠的性质,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
11.平行
【分析】长方形对边平行,有;由折叠知根据“有一组对边平行,一组对角相等的四边形是平行四边形”作出判断.
【详解】解:纸片为长方形,
∴.
∴,
由叠法知,
.
∴,
∴,
是平行四边形.
故答案为:平行.
【点睛】此题考查了平行四边形的判断,折叠的性质,关键是掌握两组对边分别平行的四边形是平行四边形.
12.6
【分析】根据翻折变换的性质、平行四边形的性质证明,此为解题的关键性结论;运用的周长为,求出的长,即可解决问题.
【详解】解:如图,四边形为平行四边形,
,;
由题意得:,;
的周长为,的周长为,
,,
,
即,
,即;
,
故答案为:.
【点睛】该题主要考查了翻折变换的性质、平行四边形的性质等几何知识点及其应用问题,解题的方法是准确找出图形中隐含的等量关系;解题的关键是灵活运用翻折变换的性质、平行四边形的性质等几何知识点来分析、判断、解答.
13.
【分析】由平行四边形的性质可得AD=BC,AB=CD=DE+CE=9,ABCD,可得∠=90°,由折叠的性质可得=DE=5,AD=,由勾股定理可求的长,AC的长.
【详解】解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD=DE+CE=9,ABCD,
∴∠BAC=∠ACD=90°,
∴∠=90°,
∵将平行四边形ABCD进行折叠,折叠后AD恰好经过点C得到,
∴=DE=5,AD=,
∴= =3,
∴=AC+3=AD=BC,
∵,
∴,
∴AC=12,
故答案为:12.
【点睛】本题考查了翻折变换,平行四边形的性质,求出的长是本题的关键.
14.115
【分析】根据以为圆心,以长为半径作弧;再以顶点为圆心,以长为半径作弧,得,,得四边形是平行四边形,根据平行四边形的性质,即可求出.
【详解】∵以为圆心,以长为半径作弧;再以顶点为圆心,以长为半径作弧
∴,
∴四边形是平行四边形
∴
∴
∵
∴
故答案为:.
【点睛】本题考查平行四边形的知识,解题的关键是熟练掌握平行四边形的判定和性质.
15.7
【分析】根据翻折变换的性质、平行四边形的性质证明AD+DC=14,此为解题的关键性结论;运用△FDA的周长为21,求出FD的长,即可解决问题.
【详解】解:∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC;
由题意得:BE=FE,AB=AF;
∵△FCE的周长为7,△FDA的周长为21,
∴CE+CF+EF=7,DF+AD+AF=21,
∴(CE+EF)+(DF+CF)+AD+AF=28,
即2(AD+DC)=28,
∴AD+DC=14,即AD+AF=14,
∴FD=21-14=7,
故答案为:7.
【点睛】本题考查了翻折变换的性质、平行四边形的性质等几何知识点及其应用问题,解题的方法是准确找出图形中隐含的等量关系;解题的关键是灵活运用翻折变换的性质、平行四边形的性质等几何知识点来分析、判断、解答.
16.18
【分析】根据平行四边形的性质得到AD∥BC,由平行线的性质得到∠AEG=∠EGF,根据折叠的性质得到∠GEF=,推出△EGF是等边三角形,于是得到结论.
【详解】解:∵四辺形ABCD是平行四辺形,
∴AD∥BC,
∴∠AEG=∠EGF,
∵将四边形沿翻折,得到,
∴∠GEF=,
∴∠AEG=60°,
∴∠EGF=60°,
∴△EGF是等边三角形,
∵EF=6,
∴△GEF的周长=18.
故答案为:18.
【点睛】此题考查平行四边形的性质,折叠的性质,等边三角形的判定及性质,熟练掌握运用这些知识点是解题关键.
17.
【分析】如图,先利用勾股定理计算出OA=,再利用基本作图和平行线的性质得到∠AOG=∠AGO,则AG=AO=,从而求解.
【详解】解:如图,∵ AOBC的顶点A的坐标为,
∴ACOB,OA=,
由作法得OG平分∠AOB,
∴∠AOG=∠BOG,
而ACOB,
∴∠AGO=∠BOG,
∴∠AOG=∠AGO,
∴AG=AO=,
故答案为:.
【点睛】本题考查了作图 基本作图,解题的关键是熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了平行四边形的性质.
18.
【分析】利用折叠的性质和平行四边形的性质得到△B′ED是等腰直角三角形,由等腰直角三角形的性质解答即可.
【详解】解:根据折叠的性质知,∠BEA=∠B′EA=45°,则∠B′ED=90°.
又由折叠的性质得BE=B′E
∵平行四边形ABCD
∴BE=DE,
∴BE=DE=B′E,
∴△B′ED是等腰直角三角形,
∴DB′=DE=×BD=.
故答案为:.
【点睛】本题考查了平行四边形的性质,等腰三角形的判定与性质以及翻折变换(折叠的性质).推知DB′=BB′是解题的关键.
19.(1)见解析
(2)
【分析】(1)先证明四边形AFCE是平行四边形,再运用有一组邻边相等的平行四边形是菱形来进行证明;
(2)作AG⊥BE于点G,因为D′F=DF,再证明DF=BE,用勾股定理分别计算BG、EB即可.
【详解】(1)解:证明:∵点C与点A重合,折痕为EF,
∴∠AEF=∠CEF,AE=EC,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF,
∴AF=EC,
又∵AF∥EC,
∴四边形AFCE是平行四边形,
又∵AE=AF,
∴四边形AFCE为菱形.
(2)如图,作AG⊥BE于点G,
则∠AGB=∠AGE=90°,
∵点D的落点为点D′,折痕为EF,
∴D'F=DF.
∵四边形ABCD为平行四边形,
∴AD=BC.
又∵AF=EC,
∴AD-AF=BC-EC,即DF=BE.
∵在Rt△AGB中,∠AGB=90°,∠B=45°,AB=,
∴AG=GB=6.
∵四边形AFCE为平行四边形,
∴AE∥FC.
∴∠AEB=∠FCE=60°.
∵在Rt△AGE中,∠AGE=90°,∠4=60°,
∴GE==,
∴BE=BG+GE=,
∴D′F=.
【点睛】本题主要考查了折叠的性质、菱形的性质与判定、勾股定理的综合运用,运用折叠的性质和平行四边形的性质发现D′F=BE是解题的关键.
20.(1)见解析
(2)10+6.
【分析】(1)由折叠的性质及平行线的性质证得BH∥DG,AD∥BC,则结论得证;
(2)设CG=x,则FG=x,BG=8-x,由勾股定理得出(8-x)2=42+x2.解方程可求得x的值,进一步计算即可求解.
【详解】(1)证明:如图,
∵四边形ABCD为矩形,
∴AB∥CD,AD∥BC,
∴∠ABD=∠CDB,
又由折叠可得:∠1=∠2,∠3=∠4,
∴∠2=∠ABD=∠CDB=∠3,
∴BH∥DG,
∵AD∥BC,
∴四边形BGDH为平行四边形;
(2)解:由折叠可得FG=CG,DF=DC=6,∠DFG=∠C=90°,
在Rt△BCD中,
∵BD2=BC2+CD2,
∴BD==10,
∴BF=10-6=4,
设CG=x,则FG=x,BG=8-x,
在Rt△BGF中,
∵BF2+FG2=BG2,42+x2=(8-x)2,
解得:x=3,
即FG=CG=3.
∴BG=8-3=5,DG==3,
∴四边形BGDH的周长为2(BG+DG)=10+6.
【点睛】本题是四边形综合题,考查了折叠的性质,平行线的性质,矩形的性质,勾股定理等知识,熟练掌握折叠的性质是解题的关键.
21.(1)EB与ED相等,证明过程见解析
(2)AC′∥BD.理由见解析
【分析】(1)依据平行线的性质以及折叠的性质,即可得到∠EDB=∠CBD,进而得出BE=DE;
(2)由BE=DE,进而得出AE=CE,再根据三角形内角和定理,即可得到∠EAC'=∠EC'A=∠EBD=∠EDB,进而得出AC'∥BD.
【详解】(1)解:EB与ED相等.
由折叠可得,∠CBD=∠C'BD,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE;
(2)解:AC′∥BD.理由如下:
∵四边形ABCD平行四边形,
∴AD=BC,
由折叠知,BC'=BC,
∴AD=BC',
由(1)知BE=DE,
∴AE=C'E,
∴∠DAC'=(180°-∠AEC')=90°-∠AEC',
同理:∠ADB=90°-∠BED,
∵∠AEC'=∠BED,
∴∠DAC'=∠ADB,
∴AC'∥BD,
故答案为:AC′∥BD.
【点睛】本题主要考查了折叠问题以及平行四边形的性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
22.(1)见解析;(2)12.
【分析】(1)根据折叠的性质得到∠CFE=∠CDE,根据平行四边形的性质得到AD∥BC,∠B=∠D,由平行线的判定得到AE∥BF,即可得到结论;
(2)根据折叠的性质得到ED=EF,则AE+AB=AE+ED=AD,从而求出四边形ABFE的周长.
【详解】(1)证明:
∵将 □ABCD沿CE折叠,使点D落在BC边上的F处,
∴∠CFE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴AE∥BF,∠B=∠CFE,
∴AB∥EF,
∴四边形ABFE为平行四边形;
(2)∵将 □ABCD沿CE折叠,使点D落在BC边上的F处,
∴DE=EF,
∵四边形ABFE为平行四边形,
∴EF=AB=ED,
∵BC=6,
∴AD=6,
∴AE+AB=AE+ED=AD=6,
∴四边形ABFE的周长=AB+BF+EF+EA=12,
故四边形ABFE的周长为:12.
【点睛】本题考查了平行四边形的判定和性质,折叠的性质,熟练掌握全等三角形及平行四边形知识是解题的关键.
23.见解析
【分析】试题分析:(1)根据翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,然后根据平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形;
(2)根据平行线的性质利用勾股定理得出答案.
【详解】(1)∵将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴ABDC,ABDC
∴CED′B,CED′B,
∴四边形BCED′是平行四边形;
(2)∵BE平分∠ABC,
∴∠CBE=∠EBA,
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AB2=AE2+BE2.
【点睛】考点:1.平行四边形的判定与性质2.勾股定理
答案第1页,共2页
答案第1页,共2页
