专题18.18平行四边形折叠问题和作图问题 培优篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题18.18平行四边形折叠问题和作图问题 培优篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-25 21:48:49 | ||
图片预览



文档简介
专题18.18 平行四边形折叠问题和作图问题
(培优篇)(专项练习)
一、单选题
1.如图,已知,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD于点F,点G为CD的中点,连接EG、BG,则=( )
A. B. C. D.
2.如图,中,对角线AC与BD相交于点E,,,将沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为,恰好,若点F为BC上一点,则的最短距离是( )
A.1 B. C. D.
3.如图,已知,在平行四边形ABCD中,∠DAB=60°,AB=4,AD=2,把平行四边形沿直线AC折叠,点B落在点E处,连接DE,则DE的长度为( )
A. B. C. D.
4.如图,在中,点E,F分别在边AB,AD上,将△AEF沿EF折叠,点A恰好落在BC边上的点G处,若,,,则AF长度为( )
A. B.7 C.6 D.20
5.如图,中,点E是AD上一点,BE⊥AB,△ABE沿BE对折得到△BEG,过点D作DF∥EG交BC于点F,△DFC沿DF对折,点C恰好与点G重合,则的值为( )
A. B. C. D.
6.如图,直线EF分别交平行四边形ABCD边AB、CD于直E、F,将图形沿直线EF对折,点A、D分别落在点A′、D′处.若∠A=60°,AD=4,AB=8,当点A′落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA′的最小值()
A.4+ B.8 C.6+ D.4
7.如图,中,,,按以下步骤作图:①以点为圆心,适当长为半径画弧,分别交于点,交于点;②分别以点,为圆心,大于的长为半径画弧,两弧在内相交于点;③画射线,交于点,交对角线于点.若,则的长度为( )
A.3 B. C. D.
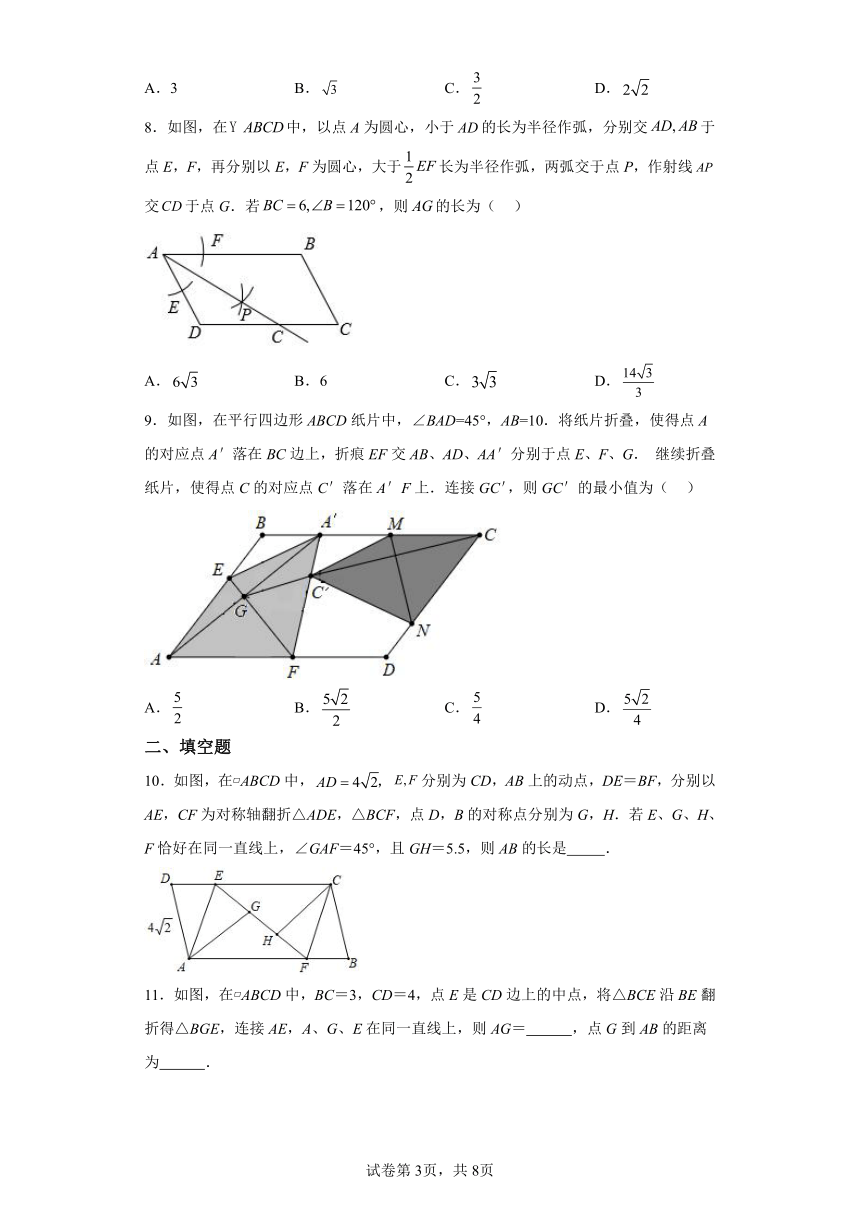
8.如图,在中,以点A为圆心,小于的长为半径作弧,分别交于点E,F,再分别以E,F为圆心,大于长为半径作弧,两弧交于点P,作射线交于点G.若,则的长为( )
A. B.6 C. D.
9.如图,在平行四边形ABCD纸片中,∠BAD=45°,AB=10.将纸片折叠,使得点A的对应点A'落在BC边上,折痕EF交AB、AD、AA'分别于点E、F、G. 继续折叠纸片,使得点C的对应点C'落在A'F上.连接GC',则GC'的最小值为( )
A. B. C. D.
二、填空题
10.如图,在 ABCD中, 分别为CD,AB上的动点,DE=BF,分别以AE,CF为对称轴翻折△ADE,△BCF,点D,B的对称点分别为G,H.若E、G、H、F恰好在同一直线上,∠GAF=45°,且GH=5.5,则AB的长是 .
11.如图,在 ABCD中,BC=3,CD=4,点E是CD边上的中点,将△BCE沿BE翻折得△BGE,连接AE,A、G、E在同一直线上,则AG= ,点G到AB的距离为 .
12.如图,在中,,,,为斜边的中点,点是射线上的一个动点,连接、,将沿着边折叠,折叠后得到,当折叠后与的重叠部分的面积恰好为面积的四分之一,则此时的长为 .
13.如图,在平面直角坐标系中,已知,C为线段的中点,点P是线段上的一个动点,连接,当的值为 时,将沿边所在直线翻折后得到的与重叠部分的面积为面积的.
14.四边形ABCD为平行四边形,已知AB=,BC=6,AC=5,点E是BC边上的动点,现将△ABE沿AE折叠,点B′是点B的对应点,设CE长为x,若点B′落在△ADE内(包括边界),则x的取值范围为 .
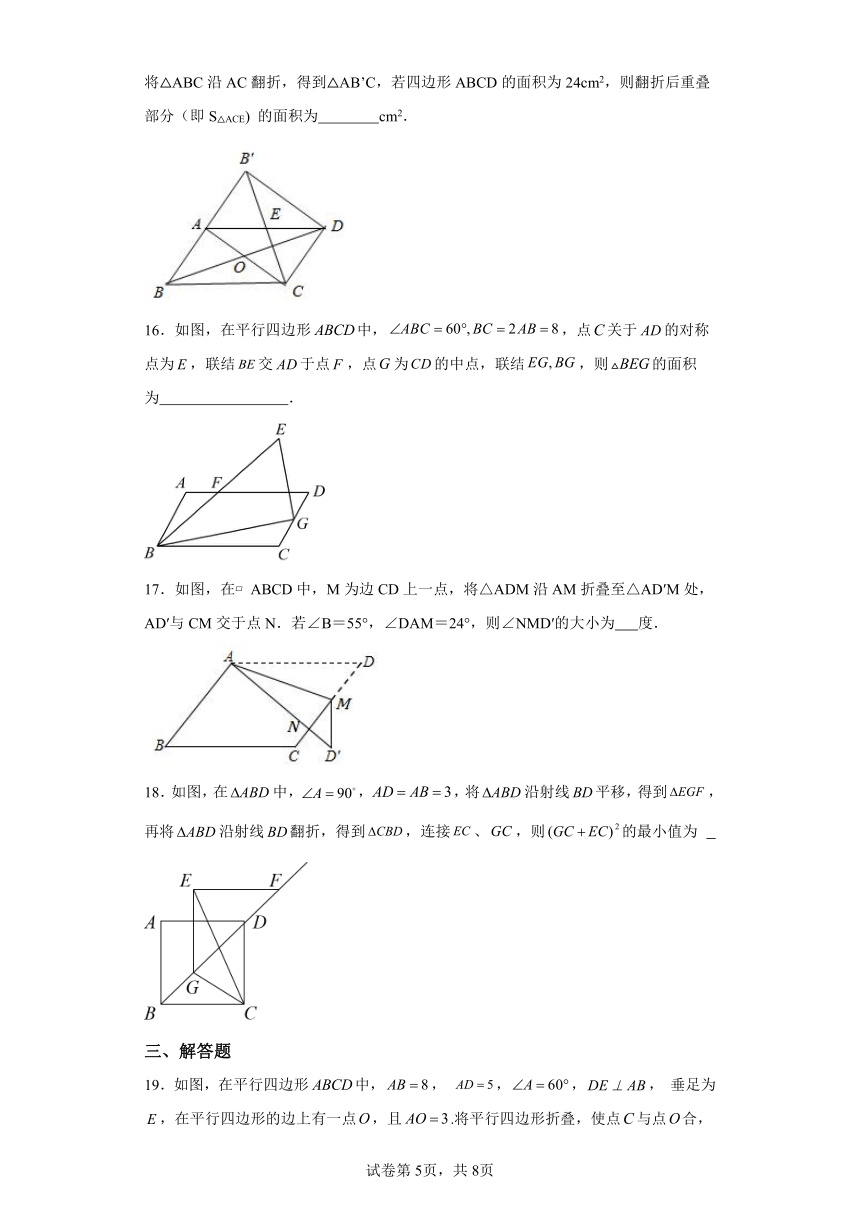
15.如图,在平行四边形ABCD中,AC⊥AB,AC与BD相交于点O,在同一平面内将△ABC沿AC翻折,得到△AB’C,若四边形ABCD的面积为24cm2,则翻折后重叠部分(即S△ACE) 的面积为 cm2.
16.如图,在平行四边形中,,点关于的对称点为,联结交于点,点为的中点,联结,则的面积为 .
17.如图,在 ABCD中,M为边CD上一点,将△ADM沿AM折叠至△AD′M处,AD′与CM交于点N.若∠B=55°,∠DAM=24°,则∠NMD′的大小为 度.
18.如图,在中,,,将沿射线平移,得到,再将沿射线翻折,得到,连接、,则的最小值为
三、解答题
19.如图,在平行四边形中,, ,,, 垂足为,在平行四边形的边上有一点,且.将平行四边形折叠,使点与点合,折痕所在直线与平行四边形交于点、.
(1)求的长;
(2)请补全图形并求折痕的长.
20.如图,在△ABC中,∠ACB=90°,AC=a,BC=b,a>b,点P是边AB上一点,连接CP,将△ACP沿CP翻折得到△QCP.
(1)若PQ⊥AB,由折叠性质可得∠BPC= °;
(2)若a=8,b=6,且PQ⊥AB,求C到AB的距离及BP的长;
(3)连接BQ,若四边形BCPQ是平行四边形,直接写出a与b之间的关系式.
21.如图1,在△ABC中,BC=6,P是BC边的一点,且不与B,C重合,将△APB沿AP折叠得,过点C作AP垂线,垂足为D,连接.
(1)AB和的数量关系是 ,AP与的位置关系是 ;
(2)如图2,当四边形是平行四边形时,求BP的长;
(3)在(2)的条件下,若BD=CD,求证:.
22.已知在中,,,点 为线段 上一点,连接.
(1)如图 1 所示,在右侧作等腰,其中,.当 , 时,求的长;
(2)如图 2 所示,在右侧作等边,连接,点为 中点,连接 交 点 .猜想线段 与之间存在的数量关系, 并证明你的猜想;
(3)如图 3, 点为中点,将沿翻折得到,连接,点 为的中点,连接.当的值最小时,连接、,直接写出的值.
23.小星在学习了轴对称的性质后,对三角形中角之间的关系进行了拓展探究.如图,在中,将沿折叠,点的对应点是点.
(1)问题解决:如图①,,当点的对应点落在的边上时,______度;
(2)问题探究:如图②,,当点的对应点落在的外部时,若,求的度数;
(3)拓展延伸:如图③,当点与点重合时,将沿折叠.点的对应点是点,与相交于点,若点是的中点,,,求的度数.
24.综合与探究:
问题情境:已知,如图1,在Rt△ABC中,∠ACB=90°,AC=BC=4.点D是AC的中点,点E在BC延长线上,且∠CDE=60°.保持△ABC不动,将△CDE从图1的位置开始,绕点C顺时针旋转α°(0<α<180)得到△CD'E',D、E的对应点分别为D'、E'.
(1)初步思考:求证:DE=AC;
(2)操作探究:如图2,当点落在DE边上时,连接AD',判断此时四边形ACE'D'的形状,并说明理由;
(3)拓展延伸:请从A,B两题中任选一题作答,我选择_____题.
A.在△CDE旋转过程中,当D'E'//BC时,请直接写出此时旋转角a的度数及B、E'两点间的距离.
B.在△CDE旋转过程中,当D'E'//AB时,延长AC交D'E'于点F,请直接写出此时旋转角α的度数及线段CF的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】取BC中点H,连接AH,连接CE交AD于N,作交CD的延长线于M,构建计算即可.
【详解】如图,取BC中点H,连接AH,连接CE交AD于N,作交CD的延长线于M,
∵,,,
∴,
∴是等边三角形,
∴,
∴,,
∵, ,
∴ , ,
∵,
∴,,
∴ ,,
∴
故选:B
【点睛】本题主要考查了平行四边形的性质,轴对称图形,等边三角形的判定和性质,解直角三角形等知识,解题的关键是正确添加辅助线构建三角形解决问题.
2.C
【分析】由折叠的性质,可得,,,由和,可得,由平行四边形和折叠的性质可求得,连接,易知是等边三角形,继而可得,然后根据平行四边形和折叠的性质可求得,利用勾股定理可求得,由垂线段最短可知,当时,最短,然后根据勾股定理即可求得答案.
【详解】解:由折叠的性质,可得:,,,
∵,
∴,
∴,
∵,
∴,
∵四边形ABCD是平行四边形,
∴AD//BC,
∴,
∴,
如图,连接,作,
∴是等边三角形,
∴,
∵四边形ABCD是平行四边形,
∴,
在中,,
∴,
由垂线段最短可知,当时,最短,
在中,,,
∴,
∴.
故选:C.
【点睛】本题主要考查了平行四边形的性质、折叠的性质、勾股定理、含30°角的直角三角形的性质、垂线段最短等,熟练掌握相关定理是解题的关键.
3.B
【分析】过点D和点C作DM⊥AB于点M,CN⊥AB延长线于点N,由翻折对称性和平行四边形的性质可得△ABC≌△AEC≌△CDA,可以证明四边形ADEC是等腰梯形,连接BE,可得AC是BE的垂直平分线,利用勾股定理可得AC的长,再根据平行四边形的面积和三角形的面积列式可得BF的长,根据勾股定理可得CF的长,进而可得DE的长.
【详解】解:如图,过点D和点C作DM⊥AB于点M,CN⊥AB延长线于点N,
由翻折对称性和平行四边形的性质可知:△ABC≌△AEC≌△CDA,
∴AD=BC=CE,∠DAC=∠BCA=∠ECA,
∴四边形ADEC是等腰梯形,
连接BE,
∵AB=AE,CB=CE,
∴AC是BE的垂直平分线,
∵,
∴CN=,BN=1,
∴AN=AB+BN=4+1=5,
∴AC===2,
∴S平行四边形ABCD=AB DM=AC BF,
∴4×=2BF,
∴BF=,
∴CF===,
在等腰梯形ADEC中,
DE=AC﹣2CF=2﹣2×=.
故选:B.
【点睛】本题考查了翻折的性质,勾股定理,平行四边形的性质,全等三角形的性质与判定,等腰梯形,含30°的直角三角形,掌握以上知识是解题的关键.
4.A
【分析】过点B作BM⊥AD于点M,过点F作FH⊥BC于点H,过点E作EN⊥CB延长线于点N,得矩形BHFM,可得△BEN和△ABM是等腰直角三角形,然后利用勾股定理即可解决问题.
【详解】解:如图,过点B作BM⊥AD于点M,过点F作FH⊥BC于点H,过点E作EN⊥CB延长线于点N,
得矩形BHFM,
∴∠MBC=90°,MB=FH,FM=BH,
∵AB=6,5BE=AE,
∴AE=5,BE=,
由折叠的性质可知:GE=AE=5,GF=AF,
∵四边形ABCD是平行四边形,
∴∠ABN=∠A=45°,
∴△BEN和△ABM是等腰直角三角形,
∴EN=BN=BE=1,AM=BM=AB=6,
∴FH=BM=6,
在Rt△GEN中,根据勾股定理,得
EN2+GN2=GE2,
∴12+GN2=(5)2,
解得GN=±7(负值舍去),
∴GN=7,
设MF=BH=x,
则GH=GN﹣BN﹣BH=7﹣1﹣x=6﹣x,GF=AF=AM+FM=6+x,
在Rt△GFH中,根据勾股定理,得
GH2+FH2=GF2,
∴(6﹣x)2+62=(6+x)2,
解得x=,
∴AF=AM+FM=6+= .
∴AF长度为 .
故答案为:A.
【点睛】本题考查了翻折变换,平行四边形的性质,等腰直角三角形的性质,勾股定理,解决本题的关键是掌握翻折的性质.
5.B
【分析】根据平行线的性质和轴对称的性质,利用SAS证明,进而得到,设AB=x,则AG=2x,CD=x,AD=,即可求解.
【详解】解:在中
∵DF∥EG
∴∠DEG=∠DFB
∵△ABE沿BE对折得到△BEG
∴∠DEG=2∠A
∵∠DFB=∠C+∠CDF
∠A=∠C
∴∠CDF=∠A
∵△DFC沿DF对折
∴∠BGE=∠DGE
BG=DG
EG=EG
∴
∵BE⊥AB
∴
设AB=x,则AG=2x,CD=x,AD=
∴
故选:B.
【点睛】此题主要考查平行线的性质、轴对称的性质、全等三角形的判断和性质、勾股定理,熟练运用平行线的性质和轴对称的性质证明是解题关键.
6.D
【分析】连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.因为A、A′关于直线EF对称,推出P′A′=P′A,推出P′A′+P′C=P′A+P′C=AC,推出当点P与P′重合时,PA′+PC的值最小,最小值=AC的长;
【详解】如图,连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.
∵A、A′关于直线EF对称,
∴P′A′=P′A,
∴P′A′+P′C=P′A+P′C=AC,
∴当点P与P′重合时,PA′+PC的值最小,最小值=AC的长.
在Rt△BCH中,∵BC=4,∠CBH=60°,
∴BH=2,CH=2,
∴AH=AB+BH=10,
在Rt△ACH中,AC=.
∴PC+PA′的最小值为,
故选:D.
【点睛】本题考查解直角三角形、轴对称最短路径问题等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用轴对称解决最短问题.
7.A
【分析】先根据平行四边形的性质得到BC=AD=10,再利用勾股定理计算出AC=8,利用基本作图得到BQ平分∠ABC,则根据角平分线的性质得到点O到BA的距离等于点O到BC的距离,接着利用三角形的面积公式得到S△ABO:S△BCO=AB:BC=OA:OC,所以OAAC.
【详解】解:∵四边形ABCD为平行四边形,
∴BC=AD=10,
∵BA⊥CA,
∴∠BAC=90°,
在Rt△ABC中,AC8,
由作法得BQ平分∠ABC,
∴点O到BA的距离等于点O到BC的距离,
∴S△ABO:S△BCO=AB:BC=6:10=3:5,
∵S△ABO:S△BCO=OA:OC,
∴OA:OC=3:5,
∴OA:AC=3:8,
∴OAAC8=3.
故选:A.
【点睛】本题考查了作角平分线,角平分线的性质,平行四边形的性质,勾股定理,掌握角平分线的性质是解题的关键.
8.A
【分析】根据作图过程可得AG平分∠DAB,再根据角平分线的性质和平行四边形的性质可证明∠DAG=∠DGA,进而得到AD=DG,过A作AM⊥CD于M,依次求出MD、AM、AG即可解决问题.
【详解】解:过A作AM⊥CD于M,
根据作图的方法可得AG平分∠DAB,
∵AG平分∠DAB,
∴∠DAG=∠BAG,
∵,,
∴CD∥AB,AD=BC=6,,
∴∠DGA=∠BAG,
∴∠DAG=∠DGA,
∴AD=DG=BC=6,
∵,
∴∠DGA=30°,∠ADM=60°,
∴在Rt△ADM中,,
∴,
∴在Rt△AGM中,,
故选:A.
【点睛】此题主要考查了平行四边形的性质、角平分线的作法、30°直角三角形的性质;根据尺规作图的步骤判断是作角平分线是解决问题的关键.
9.B
【分析】如图,作GH⊥AD,BR⊥AD,,,利用角平分线和中位线的性质求得的长度,根据垂线段最短,即可求解.
【详解】解:如图,作GH⊥AD,BR⊥AD,GP⊥A'F,A'Q⊥AD,
∵∠BAD=45°,AB=10
∴为等腰直角三角形,
由题意可得,垂直平分,,
∴,
∴,
在中,,当、两点重合时,
即的最小值为
故选:B.
【点睛】此题考查了轴对称的性质,角平分线的性质,等腰直角三角形的性质,中位线的性质,垂线段最短,解题的关键是作出合适的辅助线,灵活运用相关性质进行求解.
10.
【分析】过G点作GM⊥AF于点M,设DE=BF=x,由勾股定理求得AM与GM,再证明AF=EF,用x表示AF,FG,FM,由勾股定理列出x的方程,求得x的值,便可求得AB.
【详解】解:过G点作GM⊥AF于点M,
由折叠知AG=AD=4,
∵∠GAF=45°,
∴∠AGM=45°,
∴AM=GM==4,
∵DE=BF,
∴设DE=BF=x,则由折叠性质知,EG=DE=BF=FH=x,
∵GH=5.5
∴EF=2x+5.5,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠AED=∠BAE,
∵∠AED=∠AEG,
∴∠FAE=∠FEA,
∴AF=EF=2x+5.5,
∴AB=AF+BF=3x+5.5,MF=AF﹣AM=2x+1.5,
由勾股定理得,FG2﹣FM2=MG2,
即(x+5.5)2﹣(2x+1.5)2=42,
解得,x=3,或x=﹣ (舍),
∴AB=3x+5.5=14.5,
故答案为:14.5.
【点睛】本题考查勾股定理,平行四边形性质,方程思想的运用,属于综合提高题.
11. 2 ##
【分析】根据折叠性质和平行四边形的性质可以证明△ABG≌△EAD,可得AG=DE=2,然后利用勾股定理可得求出AF的长,进而可得GF的值.
【详解】解:如图,GF⊥AB于点F,
∵点E是CD边上的中点,
∴CE=DE=2,
由折叠可知:∠BGE=∠C,BC=BG=3,CE=GE=2,
在 ABCD中,BC=AD=3,BC∥AD,
∴∠D+∠C=180°,BG=AD,
∵∠BGE+∠AGB=180°,
∴∠AGB=∠D,
∵AB∥CD,
∴∠BAG=∠AED,
在△ABG和△EAD中,,
∴△ABG≌△EAD(AAS),
∴AG=DE=2,
∴AB=AE=AG+GE=4,
∵GF⊥AB于点F,
∴∠AFG=∠BFG=90°,
在Rt△AFG和△BFG中,
根据勾股定理,得AG2-AF2=BG2-BF2,即22-AF2=32-(4-AF)2,
解得AF=,
∴GF2=AG2-AF2=4-=,
∴GF=,
故答案为2,.
【点睛】本题考查了折叠的性质、平行四边形的性质、勾股定理等知识,证明△ABG≌△EAD是解题的关键.
12.或
【分析】根据30°角所对的直角边等于斜边的一半可求出AB,即可得到AE的值,进而根据勾股定理求出BC,分类两种情况讨论:①若与AB交于点F,连接,易得,即可得到,,从而得到四边形是平行四边形,根据平行四边形的性质即可求解;②若与BC交于点G,连接,交EP于H,同理可得,,根据三角形中位线定理可得,此时点P与点C重合,进而可求解.
【详解】解:,为斜边AB的中点,
∴AB=8,,,
①若与AB交于点F,连接,如图1所示,
由折叠可得,,,
∵点E是AB的中点,
∴,
由题意得,
,
,
,,
∴四边形是平行四边形,
,
②若与BC交于点G,连接,交EP于H,如图2所示,
同理可得,,
,
,
,
∴点P与点C重合,
∴,
故答案为:或.
【点睛】本题考查了翻折变换,轴对称图形,30°角所对的直角边等于斜边的一半,勾股定理,平行四边形的判定及性质,三角形中位线定理等知识,巧妙运用分类讨论思想是解题的关键.
13.
【分析】根据题意作出图形,根据与重叠部分的面积为面积的,得出为的中点,可得四边形为平行四边形,根据折叠的性质可得,即可求解.
【详解】解:,
,
如图,作关于的对称点,连接,,取的中点,
C为线段的中点,
,
为与重叠部分,
,
与重叠部分的面积为面积的,
过点,
对称,
,
与重叠部分的面积为面积的,
,
,
,
四边形为平行四边形,
,
对称,
,
.
故答案为:.
【点睛】本题考查了折叠的性质,勾股定理,平行四边形的性质与判定,三角形中线的性质,证明四边形为平行四边形是解题的关键.
14.≤x≤3-2
【分析】如图1,当在AD上,易证由四边形为平行四边形,得到;如图2,过点A作AG⊥BC于点G,过点D作DH⊥BC交BC的延长线于点H,当在DE上,此时∠AEB=∠AEB=∠DAE,DA=DE=,在Rt△ABG和Rt△ACG中,利用勾股定理求出BG=2,可得AG=3=DH,在Rt△DEH中,由勾股可得:EH=3,可求得CE的另一个临界值,问题得解.
【详解】解:如图1,
当在AD上,此时,,,
∴,
∵ADBC,
∴四边形为平行四边形,
∴;
如图2,过点A作AG⊥BC于点G,过点D作DH⊥BC交BC的延长线于点H,
当在DE上,此时∠AEB=∠AEB=∠DAE,
∴DA=DE=,
在Rt△ABG和Rt△ACG中,
∴
∴BG=2,
∴AG=3=DH,
在Rt△DEH中,由勾股可得:EH=3,
∴CE=3-2;
综上:x的取值范围为:≤x≤3-2.
【点睛】本题主要考查了平行四边形的性质,翻折变换,勾股定理,找到临界状态求出x的长是解题的关键.
15.6
【分析】由折叠的性质可得∠BAC=∠B'AC=90°,AB=AB',S△ABC=S△AB'C=12cm2,可证点B,点A,点B'三点共线,通过证明四边形ACDB'是平行四边形,可得B'E=CE,即可求解.
【详解】解:∵四边形ABCD是平行四边形,
∴AB∥CD,S△ABC==12cm2,
∵在同一平面内将△ABC沿AC翻折,得到△AB′C,
∴∠BAC=∠B'AC=90°,AB=AB',S△ABC=S△AB'C=12cm2,
∴∠BAB'=180°,
∴点B,点A,点B'三点共线,
∵AB∥CD,AB'∥CD,
∴四边形ACDB'是平行四边形,
∴B'E=CE,
∴S△ACE=S△AB'C=6cm2,
故答案为:6.
【点睛】本题考查了翻折变换,平行四边形的判定和性质,证明点B,点A,点B'三点共线是本题的关键.
16.
【分析】如图,取中点,联结,联结交于,作交的延长线于.先证明是等边三角形进而,,结合30°直角三角形性质可求线段长,再利用计算即可;
【详解】解:如图,取中点,联结,联结交于,作交的延长线于.
,,,
,
是等边三角形,
,
,
,
,,
,,
,
,,
,,
.
故答案为.
【点睛】本题考查平行四边形的性质、轴对称图形、勾股定理、等边三角形的判定和性质、直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线构造直角三角形(含30°或45°)解决问题,属于中考常考题型.
17.22.
【分析】由平行四边形的性质得出∠D=∠B=55°,由折叠的性质得:∠D'=∠D=55°,∠MAD'=∠DAM=24°,由三角形的外角性质求出∠AMN=79°,与三角形内角和定理求出∠AMD'=101°,即可得出∠NMD'的大小.
【详解】解:∵四边形ABCD是平行四边形,
∴∠D=∠B=55°,
由折叠的性质得:∠D'=∠D=55°,∠MAD'=∠DAM=24°,
∴∠AMN=∠D+∠DAM=55°+24°=79°,∠AMD'=180°-∠MAD'-∠D'=101°,
∴∠NMD'=101°-79°=22°;
故答案为22.
【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AMN和∠AMD'是解决问题的关键.
18.45
【分析】连接,作点D关于直线的对成点T,连接、、.首先证明B、A、T共线,求出,证明四边形EGCD是平行四边形,推出,进而得到,根据,即可解决问题.
【详解】解:如图,连接、,作点D关于直线的对成点T,连接、、.
∵,,将沿射线平移,得到,再将沿射线翻折,得到,
∴,,,
∵,
∴,
∵D、T关于对称,
∴,,
∴,
∵,
∴B、A、T共线,
∴,
∵, ,
∴四边形EGCD是平行四边形,
∴,
∴,
∵,
∴,
∴,
则的最小值为45.
故答案为:45.
【点睛】本题考查轴对称,等腰三角形的性质,平行四边形的判定和性质,解直角三角形等知识,解题的关键是学会运用转化的思想思考问题.
19.(1);(2)补全图形见解析;折痕的长为5或.
【分析】(1)在Rt△ADE中,,,求得,再根据勾股定理即可求解;
(2)分点O在AB和AD两类讨论,当点在上时,可得是等边三角形.求得;点点O在AD上时,过点、分别作, ,
垂足分别为、, 连接,.求出,,,根据折叠性质,结合勾股定理,求出,进而求出,利用面积法即可求得.
【详解】(1)∵,, ,
∴.
∴.
∴.
(2)如图1所示,当点在上时,
∵, ,
∴.
∵四边形是平行四边形,
∴,, .
∴.
∵将平行四边形折叠,使点与点重合,
∴折痕垂直平分,即,
.
∵折痕与平行四边形的边交于点,
∴点与点重合.
∵,
∴.
∴.
∴.
∵,
∴是等边三角形.
∴.
如图2所示,当点在上时,
过点、分别作, ,
垂足分别为、, 连接,.
∵四边形是平行四边形,,
∴,,
∴,
∵, ,
∴.
∵在中, ,
∴.
∴,
.
∴在中,,
由折叠可知,,.
∴在中,,
即.
∴.
∴,,
∴.
∴四边形为矩形.
∴,
∵,
∴
∴.
综上所述,折痕的长为5或.
【点睛】(1)见60°角一般转化为直角三角形或等边三角形解决问题;
(2)点在平行四边形的边上,要根据题意进行分类讨论求解.
20.(1)45°;(2)CH=;(3)a=.
【分析】(1)先由翻折的性质可得,再由题意可得=90°,进而得到∠APC=135°,最后根据邻补角的性质即可解答;
(2)如图,作CH⊥AB于H,先说明CH=PH,再求出AB,最后根据等面积法列方程解答即可;
(3)如图:连接BQ,由翻折的性质可得:PA=PQ、∠QPC=∠APC,再利用平行四边形的性质得到∠QPC+∠PCB=180°进而得到∠PCB=∠BPC,即PB=BC=AP=b、AB=2b,最后运用勾股定理即可解答.
【详解】(1)证明:由翻折的性质可得
∵PQ⊥AB
∴=90°
∵180°,
∴
∴∠APC=135°
∴∠BPC=180°-∠APC=45°;
(2)如图,作CH⊥AB于H
由翻折的性质可知:∠APC=∠QPC
∵CH⊥AB,∠BPC=45°
∴CH=PH
在Rt△ABC中,
∵,即
∴CH=;
(3)如图:连接BQ
由翻折的性质可得:PA=PQ,∠QPC=∠APC
∵四边形BCPQ是平行四边形
∴PQ=BC=PA=b,PQ//BC,
∴∠QPC+∠PCB=180°
∵∠BPC+∠APC=180°
∴∠PCB=∠BPC
∴PB=BC=b
∴AP=PB=b,AB=2b,
在Rt△ABC中,则有(2b)2=a2+b2
∴a2=3b2
∵a>0.b>0,
∴a=.
【点睛】本题主要考查了翻折变换、勾股定理、平行四边形的性质等知识,解正确辅助线、构造直角三角形成为解答本题的关键.
21.(1),
(2)2
(3)详见解析
【分析】(1)由轴对称的性质即可得到,;
(2)延长AP交于E,由△APB沿AP折叠得,有,根据四边形 是平行四边形,可得==,即得BP=BC=2;
(3)连接交BC于G,由勾股定理可得CD=2,再求出DP==2,BE=,PE==1,在中,,可得,中,可得,从而,而,即可证得.
【详解】(1)解:∵△APB沿AP折叠得,
∴直线AP是的对称轴,
∴,
故答案为:AB=AB',AP⊥BB';
(2)延长AP交于E,作CP中点T,PD中点K,连接KT,则KT是△PCD的中位线,如图:
∵△APB沿AP折叠得,
∴,即,
∵四边形是平行四边形,
∴,
∵KT是△PCD的中位线,
∴,KT=CD,
∴BE=KT,,
∴∠PBE=∠PTK,∠PKT=∠PEB,
∴△BEP≌△TKP(ASA),
∴BP=PT,
∴BP=PT=CT=BC,
而BC=6,
∴BP=BC=2;
(3)连接交BC于G,如图:
由(2)知:四边形是平行四边形,BP=2,
∴PC=BC﹣BP=4,
∵BD=CD,
∴四边形是菱形,
∴,BG=CG=BC=3,
∵CD⊥AP,
∴∠DGC=∠PDC=90°,
由勾股定理可得,,
∴,即 ,
解得DG=(负值舍去),
∴CD=2,DP=2,
由(2)知:,
∴BE=,
在Rt△BPE中,PE==1,
∴DE=DP+PE=3,
Rt△ABE中,,
∴,
Rt△ADC中,,
∴,
而,
∴.
【点睛】本题考查对称变换,涉及平行四边形、菱形的性质与判定,勾股定理的应用等知识,解题的关键是勾股定理的灵活运用,表达出.
22.(1)
(2),理由见解析
(3)
【分析】(1)如图1中,过点作与点,证明推出,,解直角三角形求出,,可得结论;
(2)结论:,理由如下:如图2中,延长到,使得,连接,,,以为边向下作等边,连接,,利用全等三角形的性质证明,,可得结论;
(3)如图3中,连接,取的中点,连接,,由,推出当点落在上,的值最小,如图4中,设,则,,,利用三角形的中线的性质求出的面积和四边形的面积,可得结论.
【详解】(1)如图1中,过点作与点,
,
,
,
,
,,
,
在和中
,
,,
,
,
,
,,
,
,
.
故答案为:.
(2)结论:,理由如下:
如图2中,延长到,使得,连接,,,以为边向下作等边,连接,,
是等边三角形,
,,
,
,
,
,
,
,
,
,
,
,,
,
,
,,
四边形是平行四边形,
,,,,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
(3)如图3中,连接,取的中点,连接,
,,
定值,
是定值,
,
当点落在上,的值最小,如图4中,
设,则,,
,
,
,
,
,
,
,
,
,
,
.
【点睛】本题考查了等腰三角形和等边三角形的性质,勾股定理,全等三角形的判定和性质,三角形的中线的性质等知识,学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题是解本题的关键.
23.(1)
(2)
(3)
【分析】(1)利用翻折变换的性质求解即可;
(2)设,在中,利用三角形内角和定理,构建方程求解;
(3)如图中,连接,,延长交于点.求出,利用全等三角形的性质证明四边形是平行四边形即可.
【详解】(1)解:如图中,
由翻折变换的性质可知,,
,
.
故答案为:.
(2)如图中,设.
,,
,
由翻折变换的性质可知,,
,
,
,
.
(3)如图中,连接,,延长交于点.
由翻折变换的性质可知,,,
,
,
,
,,
,
,
,
,
,
,,
≌,
,
,
四边形是平行四边形,
,
.
【点睛】本题属于几何变换综合题,考查了翻折变换,等腰三角形的判定和性质,平行四边形的判定和性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
24.(1)见解析
(2)四边形是平行四边形,理由见解析
(3)A:旋转角的度数为150°;B,E两点间的距离为2.B:旋转角的度数为105°;线段CF的长为
【分析】(1)由含30°角直角三角形的性质可得DE=2CD,再由D是中点即可得到结论;
(2)由旋转的性质及(1)得,且,从而可得,则由平行四边形的判定即可证得结论;
(3)选择A:如图3,连接,由旋转的性质及平行线的性质可得,则可求得的度数,从而得到旋转角的度数;再由及已知可得四边形是平行四边形,从而可得;
选择B:如图4,过点C作,由平行条件可得∠CFG=45°,再由旋转性质及三角形外角的性质可求得的度数,即旋转角的度数;分别在与中即可求得CF的长.
【详解】(1)∵∠ACB=90°,
∴∠DCE=90°,
∴∠E=90° ∠CDE=30°,
∴DE=2CD,
∵D是AC的中点,
∴AC=2CD,
∴DE=AC;
(2)四边形是平行四边形,理由如下:
由旋转的性质得:,,,
由(1)知,DE=AC,
∴,
∵,,
∴是等边三角形,
∴,
∴,
∴,
∴四边形是平行四边形;
(3)选择A:如图3,由旋转的性质得:,
∵D'E'//BC,
∴,
∴,
即,
连接,
∵AC=BC,AC=DE,,
∴
∵D'E'//BC,
∴四边形是平行四边形,
∴,
∵D是AC的中点,
∴,
∴;
选择B:如图4,过点C作于G,
∵AB=AC,∠ACB=90°,
∴∠A=45°,
∵D'E'//AB,
∴∠CFG=∠A= 45°,
∵,
∴,
即旋转角α的度数为105°;
∵,,∠CFG = 45°,
∴,,
∴,CG=FG,
在中,由勾股定理得:,
在中,由勾股定理得:.
【点睛】本题考查了旋转的性质,平行四边形的判定与性质,勾股定理,等边三角形的判定与性质,等腰三角形的判定,含30°角直角三角形的性质,平行线的性质等知识,具有一定的综合性,灵活运用这些知识是解决问题的关键.
答案第1页,共2页
答案第1页,共2页
(培优篇)(专项练习)
一、单选题
1.如图,已知,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD于点F,点G为CD的中点,连接EG、BG,则=( )
A. B. C. D.
2.如图,中,对角线AC与BD相交于点E,,,将沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为,恰好,若点F为BC上一点,则的最短距离是( )
A.1 B. C. D.
3.如图,已知,在平行四边形ABCD中,∠DAB=60°,AB=4,AD=2,把平行四边形沿直线AC折叠,点B落在点E处,连接DE,则DE的长度为( )
A. B. C. D.
4.如图,在中,点E,F分别在边AB,AD上,将△AEF沿EF折叠,点A恰好落在BC边上的点G处,若,,,则AF长度为( )
A. B.7 C.6 D.20
5.如图,中,点E是AD上一点,BE⊥AB,△ABE沿BE对折得到△BEG,过点D作DF∥EG交BC于点F,△DFC沿DF对折,点C恰好与点G重合,则的值为( )
A. B. C. D.
6.如图,直线EF分别交平行四边形ABCD边AB、CD于直E、F,将图形沿直线EF对折,点A、D分别落在点A′、D′处.若∠A=60°,AD=4,AB=8,当点A′落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA′的最小值()
A.4+ B.8 C.6+ D.4
7.如图,中,,,按以下步骤作图:①以点为圆心,适当长为半径画弧,分别交于点,交于点;②分别以点,为圆心,大于的长为半径画弧,两弧在内相交于点;③画射线,交于点,交对角线于点.若,则的长度为( )
A.3 B. C. D.
8.如图,在中,以点A为圆心,小于的长为半径作弧,分别交于点E,F,再分别以E,F为圆心,大于长为半径作弧,两弧交于点P,作射线交于点G.若,则的长为( )
A. B.6 C. D.
9.如图,在平行四边形ABCD纸片中,∠BAD=45°,AB=10.将纸片折叠,使得点A的对应点A'落在BC边上,折痕EF交AB、AD、AA'分别于点E、F、G. 继续折叠纸片,使得点C的对应点C'落在A'F上.连接GC',则GC'的最小值为( )
A. B. C. D.
二、填空题
10.如图,在 ABCD中, 分别为CD,AB上的动点,DE=BF,分别以AE,CF为对称轴翻折△ADE,△BCF,点D,B的对称点分别为G,H.若E、G、H、F恰好在同一直线上,∠GAF=45°,且GH=5.5,则AB的长是 .
11.如图,在 ABCD中,BC=3,CD=4,点E是CD边上的中点,将△BCE沿BE翻折得△BGE,连接AE,A、G、E在同一直线上,则AG= ,点G到AB的距离为 .
12.如图,在中,,,,为斜边的中点,点是射线上的一个动点,连接、,将沿着边折叠,折叠后得到,当折叠后与的重叠部分的面积恰好为面积的四分之一,则此时的长为 .
13.如图,在平面直角坐标系中,已知,C为线段的中点,点P是线段上的一个动点,连接,当的值为 时,将沿边所在直线翻折后得到的与重叠部分的面积为面积的.
14.四边形ABCD为平行四边形,已知AB=,BC=6,AC=5,点E是BC边上的动点,现将△ABE沿AE折叠,点B′是点B的对应点,设CE长为x,若点B′落在△ADE内(包括边界),则x的取值范围为 .
15.如图,在平行四边形ABCD中,AC⊥AB,AC与BD相交于点O,在同一平面内将△ABC沿AC翻折,得到△AB’C,若四边形ABCD的面积为24cm2,则翻折后重叠部分(即S△ACE) 的面积为 cm2.
16.如图,在平行四边形中,,点关于的对称点为,联结交于点,点为的中点,联结,则的面积为 .
17.如图,在 ABCD中,M为边CD上一点,将△ADM沿AM折叠至△AD′M处,AD′与CM交于点N.若∠B=55°,∠DAM=24°,则∠NMD′的大小为 度.
18.如图,在中,,,将沿射线平移,得到,再将沿射线翻折,得到,连接、,则的最小值为
三、解答题
19.如图,在平行四边形中,, ,,, 垂足为,在平行四边形的边上有一点,且.将平行四边形折叠,使点与点合,折痕所在直线与平行四边形交于点、.
(1)求的长;
(2)请补全图形并求折痕的长.
20.如图,在△ABC中,∠ACB=90°,AC=a,BC=b,a>b,点P是边AB上一点,连接CP,将△ACP沿CP翻折得到△QCP.
(1)若PQ⊥AB,由折叠性质可得∠BPC= °;
(2)若a=8,b=6,且PQ⊥AB,求C到AB的距离及BP的长;
(3)连接BQ,若四边形BCPQ是平行四边形,直接写出a与b之间的关系式.
21.如图1,在△ABC中,BC=6,P是BC边的一点,且不与B,C重合,将△APB沿AP折叠得,过点C作AP垂线,垂足为D,连接.
(1)AB和的数量关系是 ,AP与的位置关系是 ;
(2)如图2,当四边形是平行四边形时,求BP的长;
(3)在(2)的条件下,若BD=CD,求证:.
22.已知在中,,,点 为线段 上一点,连接.
(1)如图 1 所示,在右侧作等腰,其中,.当 , 时,求的长;
(2)如图 2 所示,在右侧作等边,连接,点为 中点,连接 交 点 .猜想线段 与之间存在的数量关系, 并证明你的猜想;
(3)如图 3, 点为中点,将沿翻折得到,连接,点 为的中点,连接.当的值最小时,连接、,直接写出的值.
23.小星在学习了轴对称的性质后,对三角形中角之间的关系进行了拓展探究.如图,在中,将沿折叠,点的对应点是点.
(1)问题解决:如图①,,当点的对应点落在的边上时,______度;
(2)问题探究:如图②,,当点的对应点落在的外部时,若,求的度数;
(3)拓展延伸:如图③,当点与点重合时,将沿折叠.点的对应点是点,与相交于点,若点是的中点,,,求的度数.
24.综合与探究:
问题情境:已知,如图1,在Rt△ABC中,∠ACB=90°,AC=BC=4.点D是AC的中点,点E在BC延长线上,且∠CDE=60°.保持△ABC不动,将△CDE从图1的位置开始,绕点C顺时针旋转α°(0<α<180)得到△CD'E',D、E的对应点分别为D'、E'.
(1)初步思考:求证:DE=AC;
(2)操作探究:如图2,当点落在DE边上时,连接AD',判断此时四边形ACE'D'的形状,并说明理由;
(3)拓展延伸:请从A,B两题中任选一题作答,我选择_____题.
A.在△CDE旋转过程中,当D'E'//BC时,请直接写出此时旋转角a的度数及B、E'两点间的距离.
B.在△CDE旋转过程中,当D'E'//AB时,延长AC交D'E'于点F,请直接写出此时旋转角α的度数及线段CF的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】取BC中点H,连接AH,连接CE交AD于N,作交CD的延长线于M,构建计算即可.
【详解】如图,取BC中点H,连接AH,连接CE交AD于N,作交CD的延长线于M,
∵,,,
∴,
∴是等边三角形,
∴,
∴,,
∵, ,
∴ , ,
∵,
∴,,
∴ ,,
∴
故选:B
【点睛】本题主要考查了平行四边形的性质,轴对称图形,等边三角形的判定和性质,解直角三角形等知识,解题的关键是正确添加辅助线构建三角形解决问题.
2.C
【分析】由折叠的性质,可得,,,由和,可得,由平行四边形和折叠的性质可求得,连接,易知是等边三角形,继而可得,然后根据平行四边形和折叠的性质可求得,利用勾股定理可求得,由垂线段最短可知,当时,最短,然后根据勾股定理即可求得答案.
【详解】解:由折叠的性质,可得:,,,
∵,
∴,
∴,
∵,
∴,
∵四边形ABCD是平行四边形,
∴AD//BC,
∴,
∴,
如图,连接,作,
∴是等边三角形,
∴,
∵四边形ABCD是平行四边形,
∴,
在中,,
∴,
由垂线段最短可知,当时,最短,
在中,,,
∴,
∴.
故选:C.
【点睛】本题主要考查了平行四边形的性质、折叠的性质、勾股定理、含30°角的直角三角形的性质、垂线段最短等,熟练掌握相关定理是解题的关键.
3.B
【分析】过点D和点C作DM⊥AB于点M,CN⊥AB延长线于点N,由翻折对称性和平行四边形的性质可得△ABC≌△AEC≌△CDA,可以证明四边形ADEC是等腰梯形,连接BE,可得AC是BE的垂直平分线,利用勾股定理可得AC的长,再根据平行四边形的面积和三角形的面积列式可得BF的长,根据勾股定理可得CF的长,进而可得DE的长.
【详解】解:如图,过点D和点C作DM⊥AB于点M,CN⊥AB延长线于点N,
由翻折对称性和平行四边形的性质可知:△ABC≌△AEC≌△CDA,
∴AD=BC=CE,∠DAC=∠BCA=∠ECA,
∴四边形ADEC是等腰梯形,
连接BE,
∵AB=AE,CB=CE,
∴AC是BE的垂直平分线,
∵,
∴CN=,BN=1,
∴AN=AB+BN=4+1=5,
∴AC===2,
∴S平行四边形ABCD=AB DM=AC BF,
∴4×=2BF,
∴BF=,
∴CF===,
在等腰梯形ADEC中,
DE=AC﹣2CF=2﹣2×=.
故选:B.
【点睛】本题考查了翻折的性质,勾股定理,平行四边形的性质,全等三角形的性质与判定,等腰梯形,含30°的直角三角形,掌握以上知识是解题的关键.
4.A
【分析】过点B作BM⊥AD于点M,过点F作FH⊥BC于点H,过点E作EN⊥CB延长线于点N,得矩形BHFM,可得△BEN和△ABM是等腰直角三角形,然后利用勾股定理即可解决问题.
【详解】解:如图,过点B作BM⊥AD于点M,过点F作FH⊥BC于点H,过点E作EN⊥CB延长线于点N,
得矩形BHFM,
∴∠MBC=90°,MB=FH,FM=BH,
∵AB=6,5BE=AE,
∴AE=5,BE=,
由折叠的性质可知:GE=AE=5,GF=AF,
∵四边形ABCD是平行四边形,
∴∠ABN=∠A=45°,
∴△BEN和△ABM是等腰直角三角形,
∴EN=BN=BE=1,AM=BM=AB=6,
∴FH=BM=6,
在Rt△GEN中,根据勾股定理,得
EN2+GN2=GE2,
∴12+GN2=(5)2,
解得GN=±7(负值舍去),
∴GN=7,
设MF=BH=x,
则GH=GN﹣BN﹣BH=7﹣1﹣x=6﹣x,GF=AF=AM+FM=6+x,
在Rt△GFH中,根据勾股定理,得
GH2+FH2=GF2,
∴(6﹣x)2+62=(6+x)2,
解得x=,
∴AF=AM+FM=6+= .
∴AF长度为 .
故答案为:A.
【点睛】本题考查了翻折变换,平行四边形的性质,等腰直角三角形的性质,勾股定理,解决本题的关键是掌握翻折的性质.
5.B
【分析】根据平行线的性质和轴对称的性质,利用SAS证明,进而得到,设AB=x,则AG=2x,CD=x,AD=,即可求解.
【详解】解:在中
∵DF∥EG
∴∠DEG=∠DFB
∵△ABE沿BE对折得到△BEG
∴∠DEG=2∠A
∵∠DFB=∠C+∠CDF
∠A=∠C
∴∠CDF=∠A
∵△DFC沿DF对折
∴∠BGE=∠DGE
BG=DG
EG=EG
∴
∵BE⊥AB
∴
设AB=x,则AG=2x,CD=x,AD=
∴
故选:B.
【点睛】此题主要考查平行线的性质、轴对称的性质、全等三角形的判断和性质、勾股定理,熟练运用平行线的性质和轴对称的性质证明是解题关键.
6.D
【分析】连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.因为A、A′关于直线EF对称,推出P′A′=P′A,推出P′A′+P′C=P′A+P′C=AC,推出当点P与P′重合时,PA′+PC的值最小,最小值=AC的长;
【详解】如图,连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.
∵A、A′关于直线EF对称,
∴P′A′=P′A,
∴P′A′+P′C=P′A+P′C=AC,
∴当点P与P′重合时,PA′+PC的值最小,最小值=AC的长.
在Rt△BCH中,∵BC=4,∠CBH=60°,
∴BH=2,CH=2,
∴AH=AB+BH=10,
在Rt△ACH中,AC=.
∴PC+PA′的最小值为,
故选:D.
【点睛】本题考查解直角三角形、轴对称最短路径问题等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用轴对称解决最短问题.
7.A
【分析】先根据平行四边形的性质得到BC=AD=10,再利用勾股定理计算出AC=8,利用基本作图得到BQ平分∠ABC,则根据角平分线的性质得到点O到BA的距离等于点O到BC的距离,接着利用三角形的面积公式得到S△ABO:S△BCO=AB:BC=OA:OC,所以OAAC.
【详解】解:∵四边形ABCD为平行四边形,
∴BC=AD=10,
∵BA⊥CA,
∴∠BAC=90°,
在Rt△ABC中,AC8,
由作法得BQ平分∠ABC,
∴点O到BA的距离等于点O到BC的距离,
∴S△ABO:S△BCO=AB:BC=6:10=3:5,
∵S△ABO:S△BCO=OA:OC,
∴OA:OC=3:5,
∴OA:AC=3:8,
∴OAAC8=3.
故选:A.
【点睛】本题考查了作角平分线,角平分线的性质,平行四边形的性质,勾股定理,掌握角平分线的性质是解题的关键.
8.A
【分析】根据作图过程可得AG平分∠DAB,再根据角平分线的性质和平行四边形的性质可证明∠DAG=∠DGA,进而得到AD=DG,过A作AM⊥CD于M,依次求出MD、AM、AG即可解决问题.
【详解】解:过A作AM⊥CD于M,
根据作图的方法可得AG平分∠DAB,
∵AG平分∠DAB,
∴∠DAG=∠BAG,
∵,,
∴CD∥AB,AD=BC=6,,
∴∠DGA=∠BAG,
∴∠DAG=∠DGA,
∴AD=DG=BC=6,
∵,
∴∠DGA=30°,∠ADM=60°,
∴在Rt△ADM中,,
∴,
∴在Rt△AGM中,,
故选:A.
【点睛】此题主要考查了平行四边形的性质、角平分线的作法、30°直角三角形的性质;根据尺规作图的步骤判断是作角平分线是解决问题的关键.
9.B
【分析】如图,作GH⊥AD,BR⊥AD,,,利用角平分线和中位线的性质求得的长度,根据垂线段最短,即可求解.
【详解】解:如图,作GH⊥AD,BR⊥AD,GP⊥A'F,A'Q⊥AD,
∵∠BAD=45°,AB=10
∴为等腰直角三角形,
由题意可得,垂直平分,,
∴,
∴,
在中,,当、两点重合时,
即的最小值为
故选:B.
【点睛】此题考查了轴对称的性质,角平分线的性质,等腰直角三角形的性质,中位线的性质,垂线段最短,解题的关键是作出合适的辅助线,灵活运用相关性质进行求解.
10.
【分析】过G点作GM⊥AF于点M,设DE=BF=x,由勾股定理求得AM与GM,再证明AF=EF,用x表示AF,FG,FM,由勾股定理列出x的方程,求得x的值,便可求得AB.
【详解】解:过G点作GM⊥AF于点M,
由折叠知AG=AD=4,
∵∠GAF=45°,
∴∠AGM=45°,
∴AM=GM==4,
∵DE=BF,
∴设DE=BF=x,则由折叠性质知,EG=DE=BF=FH=x,
∵GH=5.5
∴EF=2x+5.5,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠AED=∠BAE,
∵∠AED=∠AEG,
∴∠FAE=∠FEA,
∴AF=EF=2x+5.5,
∴AB=AF+BF=3x+5.5,MF=AF﹣AM=2x+1.5,
由勾股定理得,FG2﹣FM2=MG2,
即(x+5.5)2﹣(2x+1.5)2=42,
解得,x=3,或x=﹣ (舍),
∴AB=3x+5.5=14.5,
故答案为:14.5.
【点睛】本题考查勾股定理,平行四边形性质,方程思想的运用,属于综合提高题.
11. 2 ##
【分析】根据折叠性质和平行四边形的性质可以证明△ABG≌△EAD,可得AG=DE=2,然后利用勾股定理可得求出AF的长,进而可得GF的值.
【详解】解:如图,GF⊥AB于点F,
∵点E是CD边上的中点,
∴CE=DE=2,
由折叠可知:∠BGE=∠C,BC=BG=3,CE=GE=2,
在 ABCD中,BC=AD=3,BC∥AD,
∴∠D+∠C=180°,BG=AD,
∵∠BGE+∠AGB=180°,
∴∠AGB=∠D,
∵AB∥CD,
∴∠BAG=∠AED,
在△ABG和△EAD中,,
∴△ABG≌△EAD(AAS),
∴AG=DE=2,
∴AB=AE=AG+GE=4,
∵GF⊥AB于点F,
∴∠AFG=∠BFG=90°,
在Rt△AFG和△BFG中,
根据勾股定理,得AG2-AF2=BG2-BF2,即22-AF2=32-(4-AF)2,
解得AF=,
∴GF2=AG2-AF2=4-=,
∴GF=,
故答案为2,.
【点睛】本题考查了折叠的性质、平行四边形的性质、勾股定理等知识,证明△ABG≌△EAD是解题的关键.
12.或
【分析】根据30°角所对的直角边等于斜边的一半可求出AB,即可得到AE的值,进而根据勾股定理求出BC,分类两种情况讨论:①若与AB交于点F,连接,易得,即可得到,,从而得到四边形是平行四边形,根据平行四边形的性质即可求解;②若与BC交于点G,连接,交EP于H,同理可得,,根据三角形中位线定理可得,此时点P与点C重合,进而可求解.
【详解】解:,为斜边AB的中点,
∴AB=8,,,
①若与AB交于点F,连接,如图1所示,
由折叠可得,,,
∵点E是AB的中点,
∴,
由题意得,
,
,
,,
∴四边形是平行四边形,
,
②若与BC交于点G,连接,交EP于H,如图2所示,
同理可得,,
,
,
,
∴点P与点C重合,
∴,
故答案为:或.
【点睛】本题考查了翻折变换,轴对称图形,30°角所对的直角边等于斜边的一半,勾股定理,平行四边形的判定及性质,三角形中位线定理等知识,巧妙运用分类讨论思想是解题的关键.
13.
【分析】根据题意作出图形,根据与重叠部分的面积为面积的,得出为的中点,可得四边形为平行四边形,根据折叠的性质可得,即可求解.
【详解】解:,
,
如图,作关于的对称点,连接,,取的中点,
C为线段的中点,
,
为与重叠部分,
,
与重叠部分的面积为面积的,
过点,
对称,
,
与重叠部分的面积为面积的,
,
,
,
四边形为平行四边形,
,
对称,
,
.
故答案为:.
【点睛】本题考查了折叠的性质,勾股定理,平行四边形的性质与判定,三角形中线的性质,证明四边形为平行四边形是解题的关键.
14.≤x≤3-2
【分析】如图1,当在AD上,易证由四边形为平行四边形,得到;如图2,过点A作AG⊥BC于点G,过点D作DH⊥BC交BC的延长线于点H,当在DE上,此时∠AEB=∠AEB=∠DAE,DA=DE=,在Rt△ABG和Rt△ACG中,利用勾股定理求出BG=2,可得AG=3=DH,在Rt△DEH中,由勾股可得:EH=3,可求得CE的另一个临界值,问题得解.
【详解】解:如图1,
当在AD上,此时,,,
∴,
∵ADBC,
∴四边形为平行四边形,
∴;
如图2,过点A作AG⊥BC于点G,过点D作DH⊥BC交BC的延长线于点H,
当在DE上,此时∠AEB=∠AEB=∠DAE,
∴DA=DE=,
在Rt△ABG和Rt△ACG中,
∴
∴BG=2,
∴AG=3=DH,
在Rt△DEH中,由勾股可得:EH=3,
∴CE=3-2;
综上:x的取值范围为:≤x≤3-2.
【点睛】本题主要考查了平行四边形的性质,翻折变换,勾股定理,找到临界状态求出x的长是解题的关键.
15.6
【分析】由折叠的性质可得∠BAC=∠B'AC=90°,AB=AB',S△ABC=S△AB'C=12cm2,可证点B,点A,点B'三点共线,通过证明四边形ACDB'是平行四边形,可得B'E=CE,即可求解.
【详解】解:∵四边形ABCD是平行四边形,
∴AB∥CD,S△ABC==12cm2,
∵在同一平面内将△ABC沿AC翻折,得到△AB′C,
∴∠BAC=∠B'AC=90°,AB=AB',S△ABC=S△AB'C=12cm2,
∴∠BAB'=180°,
∴点B,点A,点B'三点共线,
∵AB∥CD,AB'∥CD,
∴四边形ACDB'是平行四边形,
∴B'E=CE,
∴S△ACE=S△AB'C=6cm2,
故答案为:6.
【点睛】本题考查了翻折变换,平行四边形的判定和性质,证明点B,点A,点B'三点共线是本题的关键.
16.
【分析】如图,取中点,联结,联结交于,作交的延长线于.先证明是等边三角形进而,,结合30°直角三角形性质可求线段长,再利用计算即可;
【详解】解:如图,取中点,联结,联结交于,作交的延长线于.
,,,
,
是等边三角形,
,
,
,
,,
,,
,
,,
,,
.
故答案为.
【点睛】本题考查平行四边形的性质、轴对称图形、勾股定理、等边三角形的判定和性质、直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线构造直角三角形(含30°或45°)解决问题,属于中考常考题型.
17.22.
【分析】由平行四边形的性质得出∠D=∠B=55°,由折叠的性质得:∠D'=∠D=55°,∠MAD'=∠DAM=24°,由三角形的外角性质求出∠AMN=79°,与三角形内角和定理求出∠AMD'=101°,即可得出∠NMD'的大小.
【详解】解:∵四边形ABCD是平行四边形,
∴∠D=∠B=55°,
由折叠的性质得:∠D'=∠D=55°,∠MAD'=∠DAM=24°,
∴∠AMN=∠D+∠DAM=55°+24°=79°,∠AMD'=180°-∠MAD'-∠D'=101°,
∴∠NMD'=101°-79°=22°;
故答案为22.
【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AMN和∠AMD'是解决问题的关键.
18.45
【分析】连接,作点D关于直线的对成点T,连接、、.首先证明B、A、T共线,求出,证明四边形EGCD是平行四边形,推出,进而得到,根据,即可解决问题.
【详解】解:如图,连接、,作点D关于直线的对成点T,连接、、.
∵,,将沿射线平移,得到,再将沿射线翻折,得到,
∴,,,
∵,
∴,
∵D、T关于对称,
∴,,
∴,
∵,
∴B、A、T共线,
∴,
∵, ,
∴四边形EGCD是平行四边形,
∴,
∴,
∵,
∴,
∴,
则的最小值为45.
故答案为:45.
【点睛】本题考查轴对称,等腰三角形的性质,平行四边形的判定和性质,解直角三角形等知识,解题的关键是学会运用转化的思想思考问题.
19.(1);(2)补全图形见解析;折痕的长为5或.
【分析】(1)在Rt△ADE中,,,求得,再根据勾股定理即可求解;
(2)分点O在AB和AD两类讨论,当点在上时,可得是等边三角形.求得;点点O在AD上时,过点、分别作, ,
垂足分别为、, 连接,.求出,,,根据折叠性质,结合勾股定理,求出,进而求出,利用面积法即可求得.
【详解】(1)∵,, ,
∴.
∴.
∴.
(2)如图1所示,当点在上时,
∵, ,
∴.
∵四边形是平行四边形,
∴,, .
∴.
∵将平行四边形折叠,使点与点重合,
∴折痕垂直平分,即,
.
∵折痕与平行四边形的边交于点,
∴点与点重合.
∵,
∴.
∴.
∴.
∵,
∴是等边三角形.
∴.
如图2所示,当点在上时,
过点、分别作, ,
垂足分别为、, 连接,.
∵四边形是平行四边形,,
∴,,
∴,
∵, ,
∴.
∵在中, ,
∴.
∴,
.
∴在中,,
由折叠可知,,.
∴在中,,
即.
∴.
∴,,
∴.
∴四边形为矩形.
∴,
∵,
∴
∴.
综上所述,折痕的长为5或.
【点睛】(1)见60°角一般转化为直角三角形或等边三角形解决问题;
(2)点在平行四边形的边上,要根据题意进行分类讨论求解.
20.(1)45°;(2)CH=;(3)a=.
【分析】(1)先由翻折的性质可得,再由题意可得=90°,进而得到∠APC=135°,最后根据邻补角的性质即可解答;
(2)如图,作CH⊥AB于H,先说明CH=PH,再求出AB,最后根据等面积法列方程解答即可;
(3)如图:连接BQ,由翻折的性质可得:PA=PQ、∠QPC=∠APC,再利用平行四边形的性质得到∠QPC+∠PCB=180°进而得到∠PCB=∠BPC,即PB=BC=AP=b、AB=2b,最后运用勾股定理即可解答.
【详解】(1)证明:由翻折的性质可得
∵PQ⊥AB
∴=90°
∵180°,
∴
∴∠APC=135°
∴∠BPC=180°-∠APC=45°;
(2)如图,作CH⊥AB于H
由翻折的性质可知:∠APC=∠QPC
∵CH⊥AB,∠BPC=45°
∴CH=PH
在Rt△ABC中,
∵,即
∴CH=;
(3)如图:连接BQ
由翻折的性质可得:PA=PQ,∠QPC=∠APC
∵四边形BCPQ是平行四边形
∴PQ=BC=PA=b,PQ//BC,
∴∠QPC+∠PCB=180°
∵∠BPC+∠APC=180°
∴∠PCB=∠BPC
∴PB=BC=b
∴AP=PB=b,AB=2b,
在Rt△ABC中,则有(2b)2=a2+b2
∴a2=3b2
∵a>0.b>0,
∴a=.
【点睛】本题主要考查了翻折变换、勾股定理、平行四边形的性质等知识,解正确辅助线、构造直角三角形成为解答本题的关键.
21.(1),
(2)2
(3)详见解析
【分析】(1)由轴对称的性质即可得到,;
(2)延长AP交于E,由△APB沿AP折叠得,有,根据四边形 是平行四边形,可得==,即得BP=BC=2;
(3)连接交BC于G,由勾股定理可得CD=2,再求出DP==2,BE=,PE==1,在中,,可得,中,可得,从而,而,即可证得.
【详解】(1)解:∵△APB沿AP折叠得,
∴直线AP是的对称轴,
∴,
故答案为:AB=AB',AP⊥BB';
(2)延长AP交于E,作CP中点T,PD中点K,连接KT,则KT是△PCD的中位线,如图:
∵△APB沿AP折叠得,
∴,即,
∵四边形是平行四边形,
∴,
∵KT是△PCD的中位线,
∴,KT=CD,
∴BE=KT,,
∴∠PBE=∠PTK,∠PKT=∠PEB,
∴△BEP≌△TKP(ASA),
∴BP=PT,
∴BP=PT=CT=BC,
而BC=6,
∴BP=BC=2;
(3)连接交BC于G,如图:
由(2)知:四边形是平行四边形,BP=2,
∴PC=BC﹣BP=4,
∵BD=CD,
∴四边形是菱形,
∴,BG=CG=BC=3,
∵CD⊥AP,
∴∠DGC=∠PDC=90°,
由勾股定理可得,,
∴,即 ,
解得DG=(负值舍去),
∴CD=2,DP=2,
由(2)知:,
∴BE=,
在Rt△BPE中,PE==1,
∴DE=DP+PE=3,
Rt△ABE中,,
∴,
Rt△ADC中,,
∴,
而,
∴.
【点睛】本题考查对称变换,涉及平行四边形、菱形的性质与判定,勾股定理的应用等知识,解题的关键是勾股定理的灵活运用,表达出.
22.(1)
(2),理由见解析
(3)
【分析】(1)如图1中,过点作与点,证明推出,,解直角三角形求出,,可得结论;
(2)结论:,理由如下:如图2中,延长到,使得,连接,,,以为边向下作等边,连接,,利用全等三角形的性质证明,,可得结论;
(3)如图3中,连接,取的中点,连接,,由,推出当点落在上,的值最小,如图4中,设,则,,,利用三角形的中线的性质求出的面积和四边形的面积,可得结论.
【详解】(1)如图1中,过点作与点,
,
,
,
,
,,
,
在和中
,
,,
,
,
,
,,
,
,
.
故答案为:.
(2)结论:,理由如下:
如图2中,延长到,使得,连接,,,以为边向下作等边,连接,,
是等边三角形,
,,
,
,
,
,
,
,
,
,
,
,,
,
,
,,
四边形是平行四边形,
,,,,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
(3)如图3中,连接,取的中点,连接,
,,
定值,
是定值,
,
当点落在上,的值最小,如图4中,
设,则,,
,
,
,
,
,
,
,
,
,
,
.
【点睛】本题考查了等腰三角形和等边三角形的性质,勾股定理,全等三角形的判定和性质,三角形的中线的性质等知识,学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题是解本题的关键.
23.(1)
(2)
(3)
【分析】(1)利用翻折变换的性质求解即可;
(2)设,在中,利用三角形内角和定理,构建方程求解;
(3)如图中,连接,,延长交于点.求出,利用全等三角形的性质证明四边形是平行四边形即可.
【详解】(1)解:如图中,
由翻折变换的性质可知,,
,
.
故答案为:.
(2)如图中,设.
,,
,
由翻折变换的性质可知,,
,
,
,
.
(3)如图中,连接,,延长交于点.
由翻折变换的性质可知,,,
,
,
,
,,
,
,
,
,
,
,,
≌,
,
,
四边形是平行四边形,
,
.
【点睛】本题属于几何变换综合题,考查了翻折变换,等腰三角形的判定和性质,平行四边形的判定和性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
24.(1)见解析
(2)四边形是平行四边形,理由见解析
(3)A:旋转角的度数为150°;B,E两点间的距离为2.B:旋转角的度数为105°;线段CF的长为
【分析】(1)由含30°角直角三角形的性质可得DE=2CD,再由D是中点即可得到结论;
(2)由旋转的性质及(1)得,且,从而可得,则由平行四边形的判定即可证得结论;
(3)选择A:如图3,连接,由旋转的性质及平行线的性质可得,则可求得的度数,从而得到旋转角的度数;再由及已知可得四边形是平行四边形,从而可得;
选择B:如图4,过点C作,由平行条件可得∠CFG=45°,再由旋转性质及三角形外角的性质可求得的度数,即旋转角的度数;分别在与中即可求得CF的长.
【详解】(1)∵∠ACB=90°,
∴∠DCE=90°,
∴∠E=90° ∠CDE=30°,
∴DE=2CD,
∵D是AC的中点,
∴AC=2CD,
∴DE=AC;
(2)四边形是平行四边形,理由如下:
由旋转的性质得:,,,
由(1)知,DE=AC,
∴,
∵,,
∴是等边三角形,
∴,
∴,
∴,
∴四边形是平行四边形;
(3)选择A:如图3,由旋转的性质得:,
∵D'E'//BC,
∴,
∴,
即,
连接,
∵AC=BC,AC=DE,,
∴
∵D'E'//BC,
∴四边形是平行四边形,
∴,
∵D是AC的中点,
∴,
∴;
选择B:如图4,过点C作于G,
∵AB=AC,∠ACB=90°,
∴∠A=45°,
∵D'E'//AB,
∴∠CFG=∠A= 45°,
∵,
∴,
即旋转角α的度数为105°;
∵,,∠CFG = 45°,
∴,,
∴,CG=FG,
在中,由勾股定理得:,
在中,由勾股定理得:.
【点睛】本题考查了旋转的性质,平行四边形的判定与性质,勾股定理,等边三角形的判定与性质,等腰三角形的判定,含30°角直角三角形的性质,平行线的性质等知识,具有一定的综合性,灵活运用这些知识是解决问题的关键.
答案第1页,共2页
答案第1页,共2页
